Función compuesta | Ejemplo 2
Summary
TLDREste vídeo educativo se enfoca en la composición de funciones, explicando cómo se halla la función compuesta de una cuadrática y una lineal. El presentador guía paso a paso a través de ejemplos prácticos, resaltando la no conmutatividad de la composición de funciones. Se recomienda ver el vídeo de introducción para comprender mejor el concepto. Además, se invita a los espectadores a practicar con ejercicios similares y a suscribirse al canal para más contenido educativo.
Takeaways
- 😀 El vídeo es una segunda lección sobre la composición de funciones.
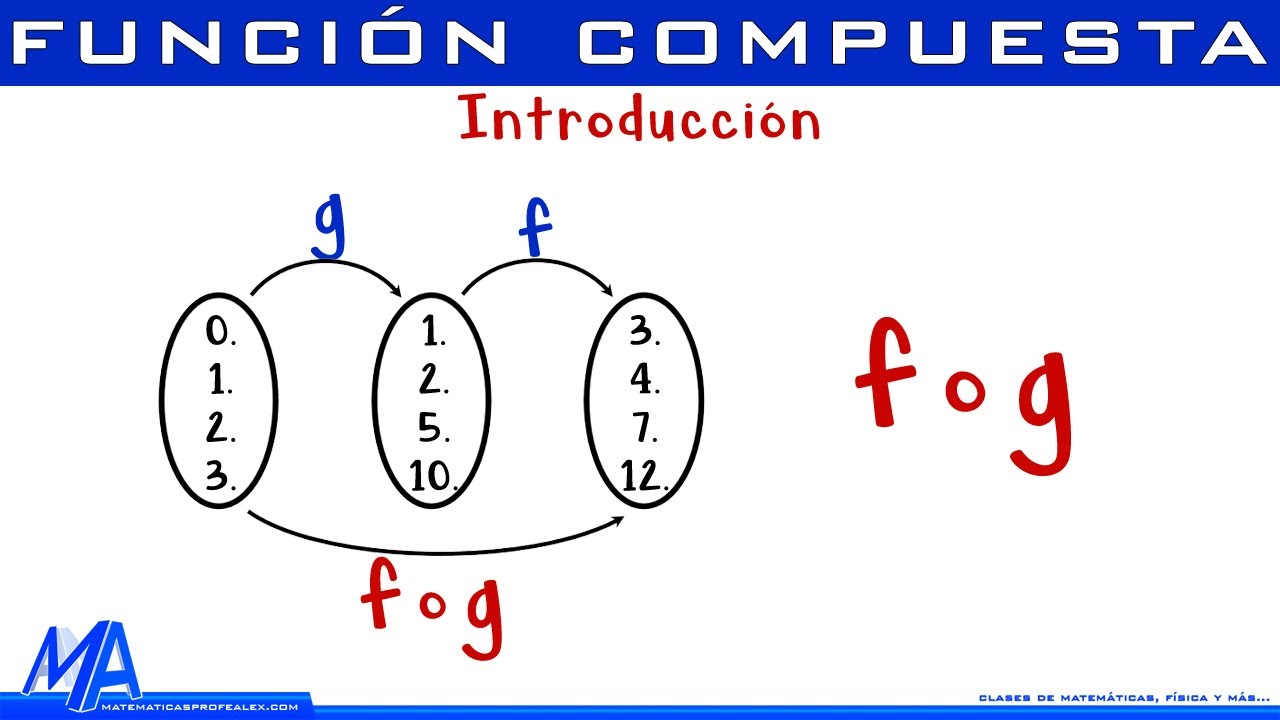
- 🔢 Se explica cómo encontrar la función compuesta de una función cuadrática (F) y una función lineal (G).
- 📝 Se aclara la diferencia entre la notación F∘G y G∘F, y que la composición de funciones no es conmutativa.
- 👩🏫 Se recomienda ver un vídeo introductorio antes de continuar si el concepto de función compuesta es nuevo.
- 📚 Se detalla el proceso de reemplazo en la función compuesta, poniendo G(x) dentro de F(x) y viceversa.
- 🔄 Se practica la sustitución de la variable independiente 'x' por la expresión '3x + 4' en la función compuesta.
- 🧮 Se resuelven ejemplos específicos para ilustrar cómo se calcula la función compuesta paso a paso.
- 📉 Se muestra la simplificación de términos en la función compuesta, incluyendo la resolución de potencias y la aplicación de la ley distributiva.
- 📖 Se invita al espectador a practicar el proceso con un ejercicio propuesto al final del vídeo.
- 📹 Se ofrecen recursos adicionales y se anima a los espectadores a suscribirse y comentar para profundizar en el tema de las funciones.
Q & A
¿Qué es la función compuesta en matemáticas?
-La función compuesta es una operación donde se toma una función y se aplica otra función a su interior. Se denota comúnmente como (f ∘ g)(x), lo que significa que primero se aplica g(x) y luego se aplica f a los resultados.
¿Cuál es la diferencia entre F compuesto G y G compuesto F en términos de notación?
-La notación para F compuesto G se escribe como f(g(x)), lo que indica que primero se aplica la función g a x y luego se aplica f al resultado. Por otro lado, G compuesto F se escribe como g(f(x)), lo que significa que primero se aplica f a x y luego se aplica g al resultado.
¿Cómo se calcula el cuadrado de un binomio en la función compuesta?
-El cuadrado de un binomio se calcula siguiendo la fórmula (a + b)^2 = a^2 + 2ab + b^2. Esto se aplica cuando se tiene un término al cuadrado que está compuesto por la suma de dos términos.
¿Qué significa 'no conmutativa' en el contexto de funciones compuestas?
-La no conmutatividad en funciones compuestas significa que el orden en que se aplican las funciones es importante y puede cambiar el resultado final. Es decir, f(g(x)) generalmente no es igual a g(f(x)).
¿Cómo se resuelve la composición de funciones cuando la función interna es lineal y la externa es cuadrática?
-Para resolver la composición de funciones donde la interna es lineal (g(x) = 3x + 4) y la externa es cuadrática (f(x) = x^2 + 2x - 1), se reemplaza la x en f(x) con la expresión de g(x), es decir, f(g(x)) = f(3x + 4), y luego se evalúa la expresión resultante.
¿Qué pasos se deben seguir para simplificar una función compuesta después de reemplazar la variable independiente?
-Después de reemplazar la variable independiente en una función compuesta, se deben seguir los siguientes pasos: 1) Evaluar potencias y productos, 2) Aplicar la ley distributiva si es necesario, 3) Combinar términos similares.
¿Cuál es la importancia de hacer las operaciones al final de la composición de funciones?
-Hacer las operaciones al final de la composición de funciones es importante para simplificar la expresión resultante y facilitar su comprensión y posterior análisis o cálculo.
¿Cómo se identifican los términos semejantes en una función compuesta para reducirlos?
-Los términos semejantes en una función compuesta son aquellos que tienen la misma parte variable con el mismo exponente. Para reducirlos, se suman o restan los coeficientes de los términos que tienen la misma parte variable.
¿Por qué es recomendable dividir el proceso de composición de funciones en pasos?
-Dividir el proceso de composición de funciones en pasos ayuda a evitar errores y facilita la comprensión de cada parte del proceso, lo que es especialmente útil cuando se trabaja con funciones complejas o en el aprendizaje de los conceptos.
¿Qué recursos adicionales se sugieren para profundizar en el estudio de funciones?
-Se sugiere ver el curso completo y otros videos relacionados con funciones para profundizar en el tema, además de participar en discusiones y compartir el conocimiento con compañeros.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)