56. Razón de cambio instantánea
Summary
TLDREl script explica el concepto de razón de cambio media y su transición a la razón de cambio instantánea en el contexto de la derivada en cálculo. Se utiliza un ejemplo de temperatura que varía con el tiempo, ilustrando cómo la razón de cambio media se calcula dividiendo el cambio en la temperatura entre el cambio en el tiempo. A través de una gráfica con puntos cada minuto, se muestra cómo la función se vuelve suave y se aproxima a la recta secante, que representa la razón de cambio instantánea. Al acercar el tiempo final al inicial, la recta secante se convierte en la tangente a la curva, representando la derivada, esencial para entender cambios en física y matemáticas.
Takeaways
- 📈 La razón de cambio media es fundamental para entender la variación de una función en un intervalo de tiempo.
- 📊 La razón de cambio instantánea se obtiene al aproximar el tiempo final al tiempo inicial, lo que se traduce en una recta tangente en lugar de una secante.
- 🕒 El delta de tiempo (Δt) se calcula como la diferencia entre el tiempo final y el tiempo inicial.
- 🌡️ El delta de temperatura (ΔT) se calcula como la temperatura final menos la temperatura inicial.
- 🔍 La razón de cambio media se representa geométricamente como el triángulo formado por los puntos de inicio y final y la recta secante.
- 📐 La recta secante es una línea que toca dos puntos de la curva y representa la razón de cambio en ese intervalo.
- 🎯 Al acercar el tiempo final al tiempo inicial, la recta secante se vuelve más vertical, lo que indica una razón de cambio más alta.
- 📉 La temperatura final puede ser más baja que la inicial, dependiendo de las condiciones, como la oscurecimiento o la noche.
- 🧮 La derivada de la temperatura respecto del tiempo es la razón de cambio instantánea y se representa cuando el intervalo de tiempo tiende a cero.
- 🌐 La derivada es una herramienta esencial en física, ciencias y matemáticas para estudiar cambios en funciones.
Q & A
¿Qué es la razón de cambio media y cómo se calcula?
-La razón de cambio media es una medida de la variación de una cantidad con respecto a otra, y se calcula dividiendo el cambio en la cantidad (delta de temperatura) entre el cambio en la otra (delta de tiempo). Geométricamente, se representa como la pendiente de la línea secante entre dos puntos en una gráfica.
¿Cuál es la diferencia entre la razón de cambio media y la razón de cambio instantánea?
-La razón de cambio media es el cambio promedio entre dos puntos, mientras que la razón de cambio instantánea es el cambio en un punto específico. La razón instantánea se obtiene tomando el límite de la razón de cambio media cuando el intervalo de tiempo tiende a cero.
¿Qué es un 'delta' en el contexto de la derivada?
-Un 'delta' (denotado como Δ) es una medida de cambio en una variable. Por ejemplo, Δt representa el cambio en el tiempo y ΔT representa el cambio en la temperatura.
¿Cómo se interpreta la inclinación de la recta secante en una gráfica?
-La inclinación de la recta secante en una gráfica representa la razón de cambio media entre dos puntos. Cuanto más vertical sea la línea, mayor será la razón de cambio, indicando un aumento o disminución más rápido de la variable dependiente.
¿Qué es la derivada de una función y cómo se relaciona con la razón de cambio instantánea?
-La derivada de una función es un concepto matemático que representa la razón de cambio instantánea de una variable con respecto a otra. Es el límite de la razón de cambio media cuando el intervalo de tiempo se hace infinitesimalmente pequeño.
¿Qué significa que la temperatura final puede ser más baja que la inicial?
-Que la temperatura final puede ser más baja que la inicial indica que la temperatura está disminuyendo, lo que podría ocurrir, por ejemplo, durante la noche cuando el sol se ha puesto y el ambiente se enfría.
¿Cómo se representa geométricamente la aproximación de la razón de cambio instantánea?
-Geométricamente, la aproximación de la razón de cambio instantánea se representa haciendo que el punto final se acerque al punto inicial en la gráfica, lo que hace que la recta secante se venga más vertical y se asemeje más a la tangente en el punto de interés.
¿Qué es la tangente en una gráfica y cómo se relaciona con la derivada?
-La tangente en una gráfica es la línea que toca la curva en un solo punto y tiene la misma inclinación que la curva en ese punto. La derivada de una función en un punto es igual a la pendiente de la tangente en ese punto.
¿Por qué es importante entender la diferencia entre la razón de cambio media y la instantánea en el estudio de funciones?
-Es importante entender esta diferencia porque la razón de cambio instantánea, representada por la derivada, es fundamental en el análisis de la tasa a la que las cosas cambian en un momento dado, lo que es crucial en áreas como la física y las ciencias.
¿Cómo se relaciona el concepto de límite con la definición de la derivada?
-El concepto de límite es esencial en la definición de la derivada, ya que la derivada se obtiene tomando el límite de la razón de cambio media cuando el intervalo de tiempo tiende a cero, lo que nos da la razón de cambio instantánea.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

LA DERIVADA COMO RAZÓN de CAMBIO (EXPLICACIÓN y DEFINICIÓN) - #1

Newton Leibniz y Usain Bolt
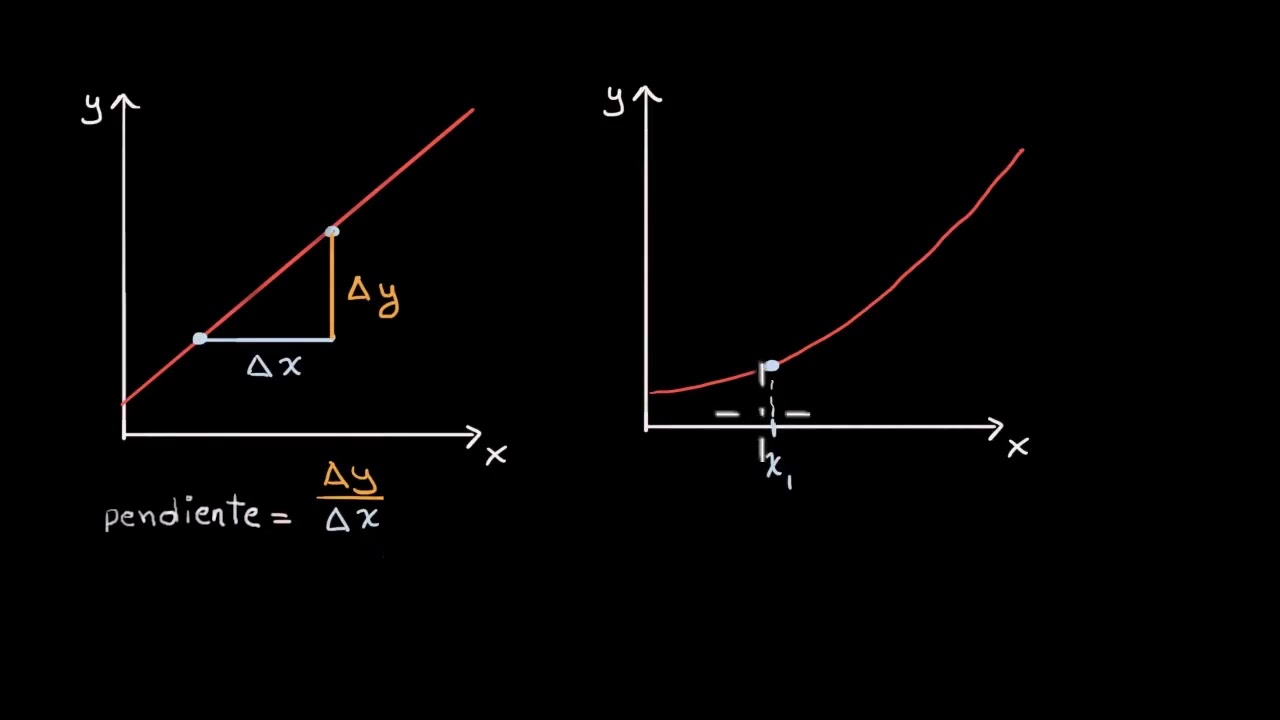
El concepto de derivada | Khan Academy en Español

PENDIENTE DE LA RECTA TANGENTE: METODO DERIVADA DE LOS 4 PASOS.

5.2: The Derivative as a Function, Part 2

El concepto de derivada. ¿Qué es y para qué sirve la derivada?
5.0 / 5 (0 votes)