Composite Functions
Summary
TLDRThis lesson delves into composite functions, contrasting them with function multiplication. It uses f(x) = 3x - 4 and g(x) = x^2 - 3 to demonstrate how to calculate f(g(x)) and g(f(x)). The process involves substituting one function into another, showcasing the steps to find f(g(x)) = 3(x^2 - 3) - 4 and g(f(x)) = (3x - 4)^2 - 3. The lesson further illustrates the evaluation of composite functions with examples, such as f(g(2)) and g(f(-1)), enhancing understanding of function composition.
Takeaways
- 🔢 Composite functions are different from function multiplication; they involve one function 'inside' another.
- 📐 The notation for composite functions is an open circle (e.g., f(g(x))) indicating that g(x) is substituted into f(x).
- 🔄 To find f(g(x)), substitute g(x) into f(x) wherever there is an x in the function f(x).
- 📘 The process of finding g(f(x)) involves substituting f(x) into g(x) wherever there is an x in the function g(x).
- 🧮 Example calculation: f(x) = 3x - 4 and g(x) = x^2 - 3 leads to f(g(x)) = 3(x^2 - 3) - 4 which simplifies to 3x^2 - 13.
- 📊 For g(f(x)), the example given is f(x) = 3x - 4 and g(x) = x^2 - 3, resulting in g(f(x)) = (3x - 4)^2 - 3 which simplifies to 9x^2 - 24x + 13.
- 📈 When evaluating composite functions at specific values, first calculate the inner function's value and then substitute it into the outer function.
- 🔑 The example for f(g(2)) with f(x) = 5x + 2 and g(x) = x^3 - 4 results in f(g(2)) = 22 after finding g(2) = 4.
- 💡 For g(f(-1)), with the same functions, it results in g(f(-1)) = -31 after finding f(-1) = -3 and substituting into g(x).
- 📚 The lesson emphasizes the importance of understanding the order of operations and the correct substitution of values in composite functions.
Q & A
What is the difference between f(x) * g(x) and f(g(x))?
-f(x) * g(x) represents the pointwise multiplication of two functions, whereas f(g(x)) is a composite function where g(x) is substituted into f(x).
What is the expression for f(g(x)) if f(x) = 3x - 4 and g(x) = x^2 - 3?
-f(g(x)) is calculated by substituting g(x) into f(x), resulting in f(g(x)) = 3(x^2 - 3) - 4, which simplifies to 3x^2 - 9 - 4, or 3x^2 - 13.
How do you find the value of g(f(x)) when f(x) = 3x - 4 and g(x) = x^2 - 3?
-To find g(f(x)), you substitute f(x) into g(x), which gives g(f(x)) = (3x - 4)^2 - 3. After expanding and simplifying, it results in 9x^2 - 24x + 16 - 3, or 9x^2 - 24x + 13.
What is the value of f(g(2)) if f(x) = 5x + 2 and g(x) = x^3 - 4?
-First, calculate g(2) which is 2^3 - 4 = 8 - 4 = 4. Then, f(g(2)) is f(4) = 5*4 + 2 = 20 + 2 = 22.
How do you evaluate g(f(-1)) given f(x) = 5x + 2 and g(x) = x^3 - 4?
-First, find f(-1) which is 5*(-1) + 2 = -5 + 2 = -3. Then, g(f(-1)) is g(-3) = (-3)^3 - 4 = -27 - 4 = -31.
What is the significance of the order of functions in composite functions?
-The order of functions in composite functions is significant as it determines which function's output becomes the input for the other function.
Can you provide an example of how to distribute a constant in a composite function?
-Yes, in the script, the constant 3 is distributed over x^2 - 3 in f(g(x)) = 3(x^2 - 3) - 4, resulting in 3x^2 - 9 - 4.
What is the FOIL method mentioned in the script, and how is it used?
-The FOIL method is used for multiplying two binomials. It stands for First, Outer, Inner, Last, and is used in the script to multiply (3x - 4)(3x - 4).
How does the script demonstrate the process of evaluating composite functions at specific values?
-The script demonstrates evaluating composite functions at specific values by first finding the inner function's value at that point and then using it as the input for the outer function.
What is the final result of g(f(-1)) as explained in the script?
-The final result of g(f(-1)) is -31, as calculated by first finding f(-1) = -3 and then substituting it into g(x) to get g(-3) = -27 - 4.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
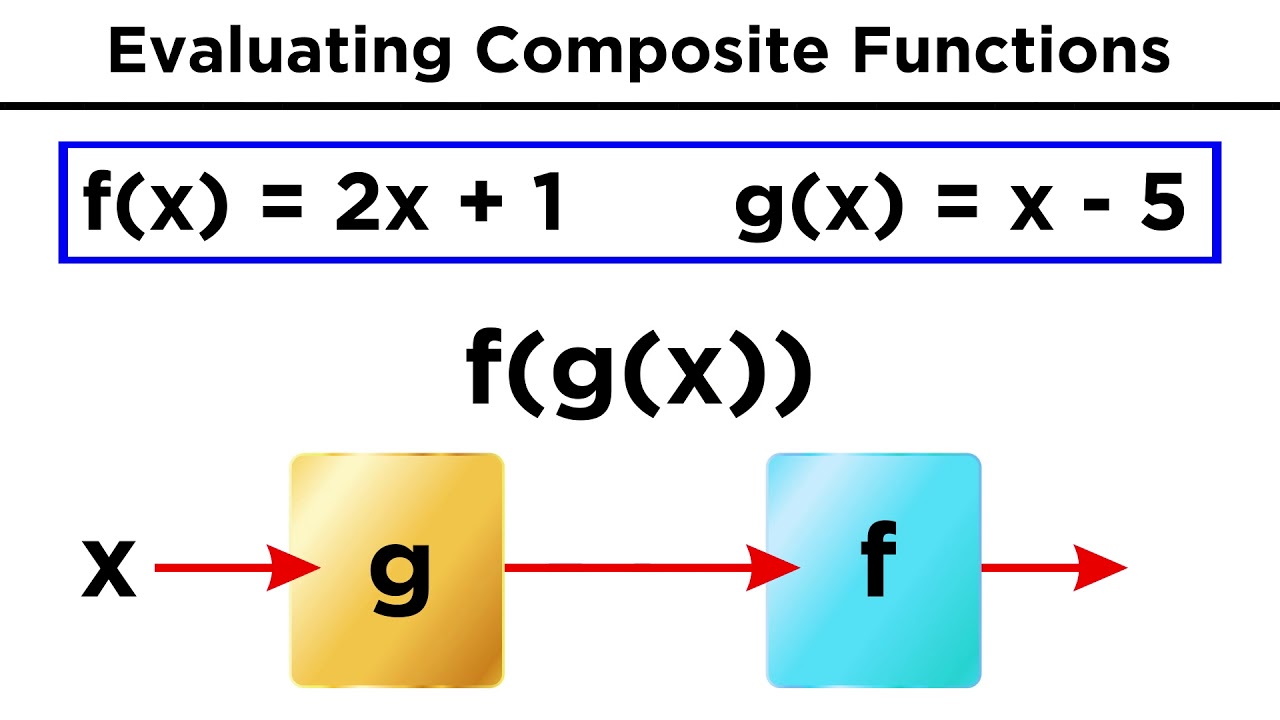
Manipulating Functions Algebraically and Evaluating Composite Functions

AP Precalculus – 2.2 Change in Linear and Exponential Functions

Composition of Function by Ma'am Ella Barrun

Invers dari Fungsi Komposisi
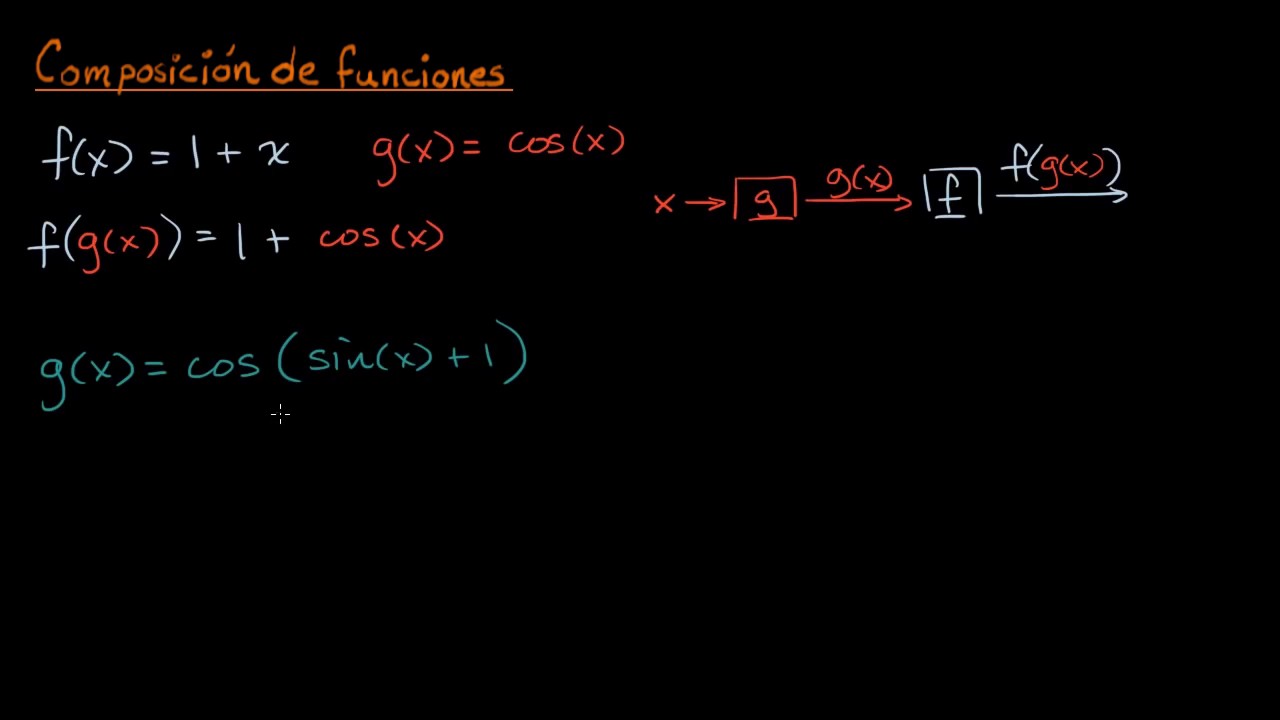
Reconocer una composición de funciones | Khan Academy en Español

FUNÇÃO | FUNÇÃO COMPOSTA - matemática 1º ensino médio | gis com giz
5.0 / 5 (0 votes)
