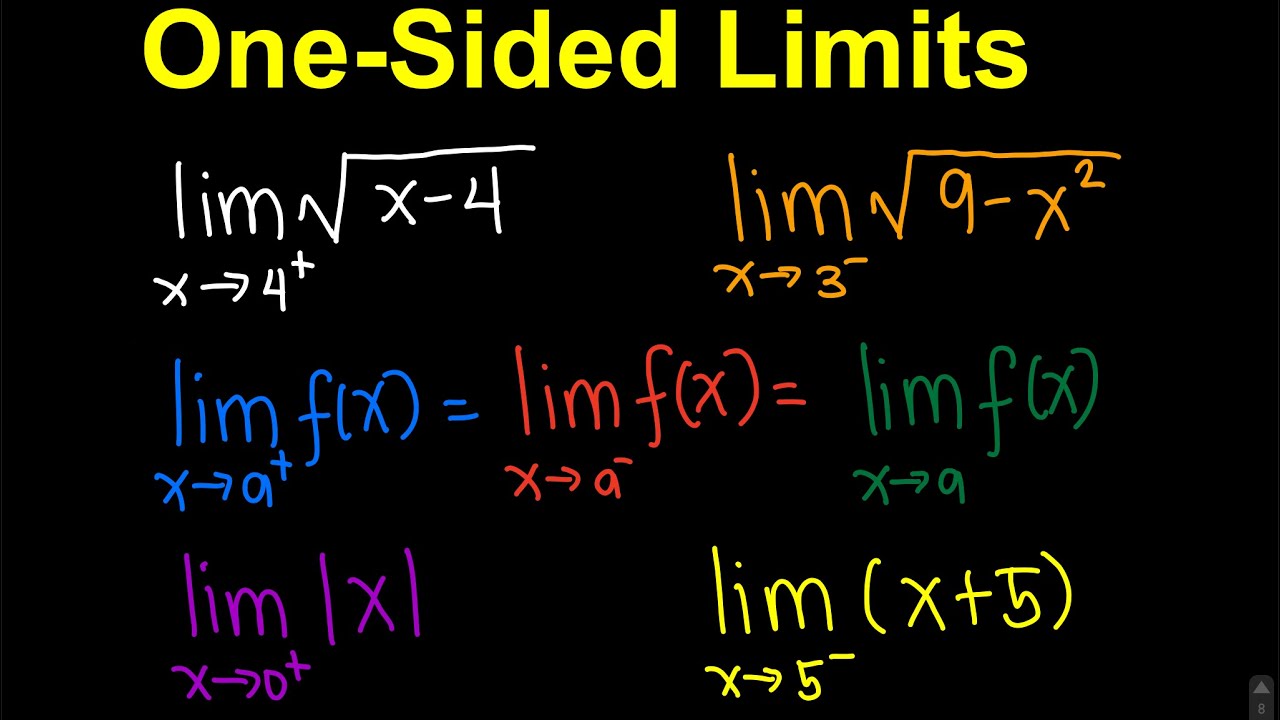Limit of a Function using a Graph - Basic/Differential Calculus

Summary

In this educational video, Sir Kenneth of STEM introduces the concept of limits in calculus, explaining how to determine the limit of a function as x approaches a certain value. He illustrates the process with examples, including left and right limits, and discusses scenarios where limits do not exist due to differing values from either side. The video also covers how to interpret limits from a graph, providing a comprehensive understanding of this fundamental calculus topic.

Takeaways

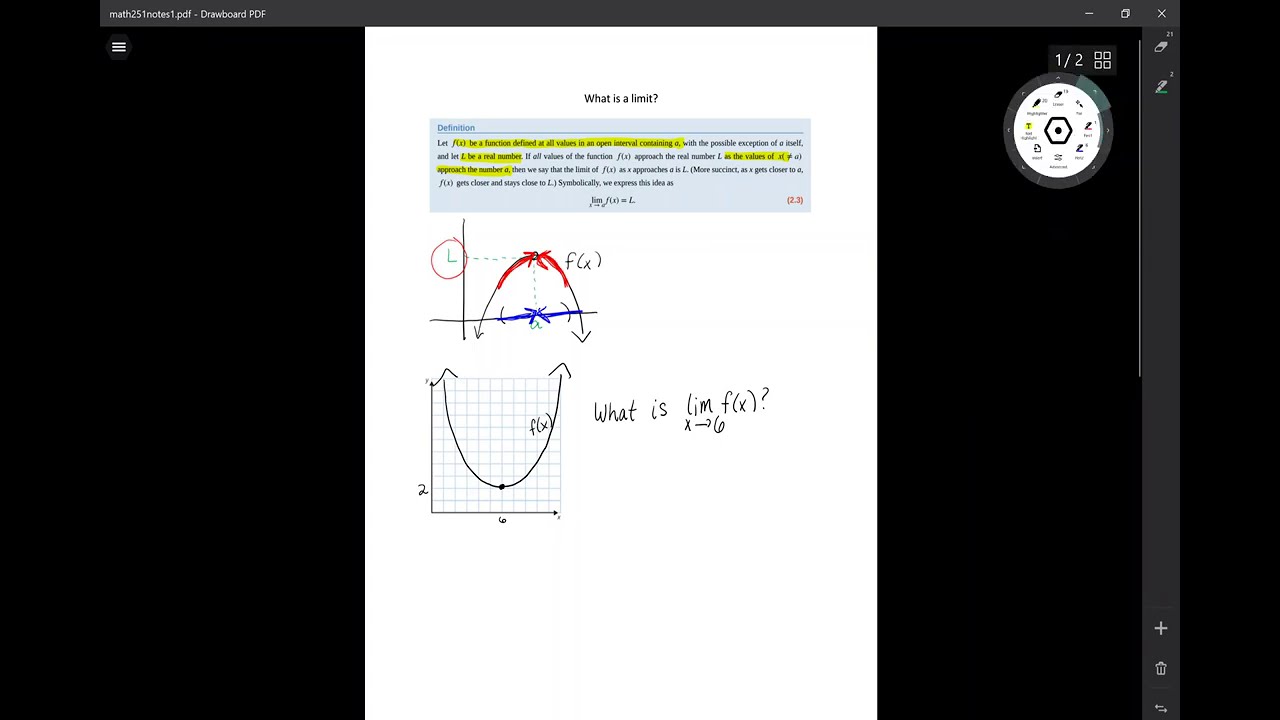
• 📚 The definition of a limit in calculus is introduced, explaining how it represents the value a function approaches as the input gets closer to a certain point.
• 🔍 The concept of left and right limits is discussed, emphasizing that if they differ, the limit at that point does not exist.
• 📈 Examples are given to illustrate how to determine the limit of a function by evaluating the left and right limits separately.
• 📉 The script demonstrates that if the left and right limits of a function at a point are the same, the limit exists and is equal to that common value.
• 🚫 It is pointed out that if the left and right limits are not equal, the limit does not exist at that point.
• 📝 The importance of the limit of a function being a single value is stressed, and the notation for expressing limits is explained.
• 📚 The script uses the function f(x) = x + 3 to show that the limit as x approaches 2 is 5, illustrating a basic limit calculation.
• 📉 An example where the limit does not exist is provided, showing how the function behaves as x approaches zero from both sides.
• 📊 The script includes graphical examples to visually represent the concept of limits and how they can be determined from a graph.
• 📌 The process of finding limits from a graph is explained, showing how to identify the behavior of a function as it approaches specific points.
• 👨‍🏫 The presenter, Sir Kenneth of STEM, uses a teaching approach to guide the audience through the concepts of limits in a structured and educational manner.

Q & A

What is the definition of a limit in calculus?

The limit of a function f(x) as x approaches a constant 'a' is the value that the function approaches as x gets closer and closer to 'a', but not necessarily equal to 'a'. It is denoted as 'lim(x→a) f(x) = L', where 'L' is the limit.

What does it mean if the left and right limits of a function at a certain point are different?

If the left and right limits of a function at a certain point are different, it indicates that the function does not have a limit at that point, meaning the function's behavior is not consistent from both sides as it approaches that point.

How can you determine the limit of a function as x approaches a certain value using a graph?

You can determine the limit of a function from a graph by observing the behavior of the function as x gets closer to the specified value from both the left and right sides. If the function values converge to a specific number, that is the limit.

What is the difference between the limit of a function and the value of the function at a point?

The limit of a function as x approaches a certain point is the value the function approaches but does not necessarily reach, while the value of the function at a point is the actual output of the function when x is exactly at that point.

Why might the limit of a function not exist at a certain point?

The limit of a function might not exist at a certain point if the function's values do not approach a consistent number as x approaches that point, or if the function is undefined at that point.

What is an example of a function where the limit does not exist?

An example from the script is a function where as x approaches zero from the left, the function approaches negative one, and from the right, it approaches positive one. Since the left and right limits are not equal, the overall limit does not exist at x=0.

How does the concept of limits relate to the behavior of a function as it approaches infinity?

The concept of limits is used to describe the behavior of a function as it approaches infinity by considering what value the function approaches in the limit as x goes to positive or negative infinity.

What is the significance of the left and right limits in determining the overall limit of a function at a point?

The left and right limits are significant because they provide information about the function's behavior approaching a point from both directions. If they are equal, it supports the existence of a limit at that point; if not, the overall limit does not exist.

Can the limit of a function be infinity?

Yes, the limit of a function can be infinity. It indicates that as x approaches a certain value, the function's values increase without bound, approaching positive or negative infinity.

What does it mean when the limit of a function as x approaches a value is equal to the function's value at that point?

When the limit of a function as x approaches a value is equal to the function's value at that point, it means the function is continuous at that point, and there is no discontinuity or abrupt change in the function's value.