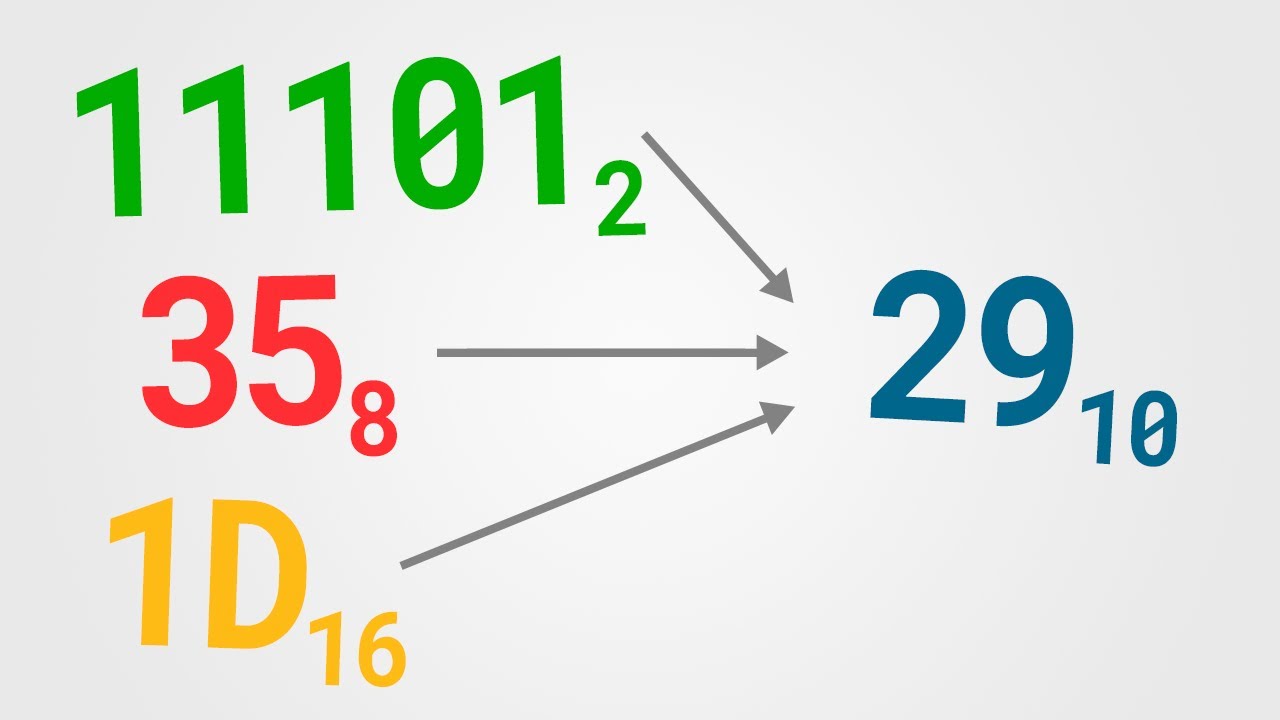
Aprender de números binarios, de manera fácil y rápida.
Summary
TLDREl guión ofrece una introducción al sistema decimal y luego se enfoca en el binario. Expone que mientras el decimal utiliza diez dígitos, el binario se basa en solo dos: 0 y 1, que representan el apagado y el encendido, respectivamente. El 0 y el 1 son la base para la computación, donde los bytes, compuestos de 8 bits, son la unidad fundamental de datos. Se explica cómo se forman combinaciones con bits y cómo se representan números decimales con bits encendidos, demostrando que cada bit encendido suma su valor correspondiente en potencia de 2, resultando en una representación eficiente de números y caracteres en la informática.
Takeaways
- 🔢 El sistema decimal es el que utilizamos en la vida cotidiana y está compuesto por diez dígitos: 0 a 9.
- 📞 Ejemplos de uso del sistema decimal son los números telefónicos, que forman millones de combinaciones con estos dígitos.
- 👀 El sistema binario es diferente, solo tiene dos dígitos: 0 y 1, representando el apagado y el encendido respectivamente.
- 💡 El 'bit' es la unidad mínima de información en informática, y su combinación permite representar diferentes estados.
- 🖇️ Un 'byte' es un grupo de 8 bits y es la unidad básica de datos en las computadoras.
- 📈 Los bytes se cuentan en potencias de 2, lo que permite calcular el número de combinaciones posibles con un número dado de bits.
- 🤔 Con dos bits, se pueden representar 4 estados (00, 01, 10, 11), y esto escala con el número de bits utilizados.
- 🔠 El número de combinaciones que se pueden formar con un cierto número de bits se calcula como 2 elevado a ese número de bits.
- 🔢 Con 3 bits, se pueden representar números del 0 al 7 en decimal, y se necesitan 4 bits para representar el número 8 en adelante.
- 👆 La importancia de los bits se mide de derecha a izquierda, con cada bit representando una potencia de 2 creciente.
- 📊 Al combinar bits encendidos y apagados, se pueden representar números decimales específicos, como se ve en el ejemplo del número 6 y 8.
Q & A
¿Qué es el sistema decimal y cómo está conformado?
-El sistema decimal es un sistema numérico que utiliza diez dígitos, desde 0 hasta 9, para representar números y se basa en potencias de 10.
¿Cómo se relacionan los números telefónicos con el sistema decimal?
-Los números telefónicos están formados por dígitos del 0 al 9, y con estos se pueden formar millones de millones de combinaciones, ilustrando la capacidad del sistema decimal para generar variaciones.
¿Cuántos dígitos utiliza el sistema binario y cuáles son?
-El sistema binario utiliza solamente dos dígitos: 0 y 1, representando el apagado y el encendido respectivamente.
¿Qué es un byte y cómo se relaciona con el sistema binario?
-Un byte es un grupo de 8 bits y es la unidad fundamental de datos en los ordenadores, siendo la unidad de capacidad de almacenamiento estándar.
¿Cómo se relaciona el número de bits con las combinaciones que se pueden formar?
-El número de combinaciones que se pueden formar con bits se basa en potencias de 2. Por ejemplo, con 2 bits se pueden formar 2^2, que es 4 combinaciones.
¿Cómo se representa el número 0 en binario?
-El número 0 en binario se representa con el dígito 0, que también puede simbolizar el apagado.
¿Cuántas combinaciones se pueden representar con 3 bits en el sistema binario?
-Con 3 bits en el sistema binario se pueden representar 2^3, que es 8 combinaciones.
¿Cómo se determina el valor decimal de una combinación de bits?
-Para determinar el valor decimal de una combinación de bits, se suman los valores correspondientes a los bits encendidos, multiplicados por su valor de potencia de 2 en la posición que ocupan.
¿Cómo se representa el número 8 en binario y cuántos bits se necesitan para ello?
-El número 8 se representa en binario como 1000, lo que requiere 4 bits.
¿Cómo se interpreta la representación de un número en binario cuando se tiene un patrón de bits encendidos y apagados?
-Se interpreta sumando los valores de los bits encendidos, donde cada bit representa una potencia de 2 correspondiente a su posición, comenzando desde la derecha (2^0, 2^1, 2^2, etc.).
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)