Komposisi Fungsi - Matematika Wajib Kelas XI Kurikulum Merdeka
Summary
TLDRThis educational video script discusses the concept of function composition in mathematics, an essential topic for 11th-grade students following the Merdeka curriculum. It explains function composition as the combination of two or more functions to form a new one, using specific rules. The script provides a step-by-step explanation of how to perform function composition, including substituting one function into another, and demonstrates this with examples using the functions f(x) = 2x + 1 and g(x) = x^2 - 3x + 4. It also emphasizes the non-commutative property of function composition, showing that the order of composition affects the outcome.
Takeaways
- 📘 The video discusses the concept of function composition in mathematics, specifically for high school curriculum.
- 🔗 Function composition is likened to the composition of products, which are made up of various ingredients or components.
- ➡️ The composition of functions involves combining two or more functions to create a new function, following specific rules.
- 📐 The operation of function composition is commonly denoted with symbols like '∘' or 'o', representing the composition or 'bundling' of functions.
- 👉 In function composition, the function on the right (e.g., f(x)) is applied first, followed by the function on the left (e.g., g(x)).
- 📊 Function composition can be visualized using an arrow diagram, illustrating the mapping from one set to another through multiple functions.
- 🔄 There are two possible compositions from two given functions: f ∘ g and g ∘ f, but they may not be commutative, meaning the order affects the result.
- 📚 The script provides a step-by-step example of how to calculate the composition of two functions, f(x) = 2x + 1 and g(x) = x^2 - 3x + 4.
- 🧮 The process involves substituting the inner function (rightmost) into the outer function (leftmost) and simplifying the expression.
- 📉 The video concludes by highlighting that the results of function composition may vary even with the same functions, emphasizing the importance of understanding the order of operations.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of function composition in mathematics, specifically for high school level 11 curriculum.
What does the term 'composition' refer to in the context of functions?
-In the context of functions, 'composition' refers to the process of combining two or more functions to create a new function, following certain rules.
How is the composition of functions denoted mathematically?
-The composition of functions is usually denoted with the symbol '∘' or 'o', and it is read as 'composition' or 'circle'.
What is the order of operations when composing functions?
-When composing functions, the function on the far right is performed first, followed by the functions on the left.
Can you provide an example of function composition from the script?
-Yes, the script provides an example with functions f(x) = 2x + 1 and g(x) = x^2 - 3x + 4. The composition of these functions is discussed.
What is the first composition of functions mentioned in the script?
-The first composition mentioned in the script is f(g(x)), which means the function g(x) is applied first, followed by f(x).
How is the composition of f(g(x)) calculated?
-The composition f(g(x)) is calculated by substituting g(x) into f(x) wherever there is an 'x', resulting in 2(g(x)) + 1.
What is the second composition of functions discussed in the script?
-The second composition discussed is g(f(x)), which means the function f(x) is applied first, followed by g(x).
How is the composition of g(f(x)) calculated?
-The composition g(f(x)) is calculated by substituting f(x) into g(x) wherever there is an 'x', resulting in g(f(x)) = (2x + 1)^2 - 3(2x + 1) + 4.
Does function composition always follow the commutative property?
-No, function composition does not always follow the commutative property. The script illustrates that f(g(x)) and g(f(x)) can yield different results even if they are composed from the same functions.
What is the final result of the composition f(g(x)) as discussed in the script?
-The final result of the composition f(g(x)) is 2x^2 - 6x + 8 + 1, which simplifies to 2x^2 - 6x + 9.
What is the final result of the composition g(f(x)) as discussed in the script?
-The final result of the composition g(f(x)) is 4x^2 - 2x - 3 + 4, which simplifies to 4x^2 - 2x + 1.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Earth Structure and Its Development | Science Material Class 8 Merdeka Curriculum
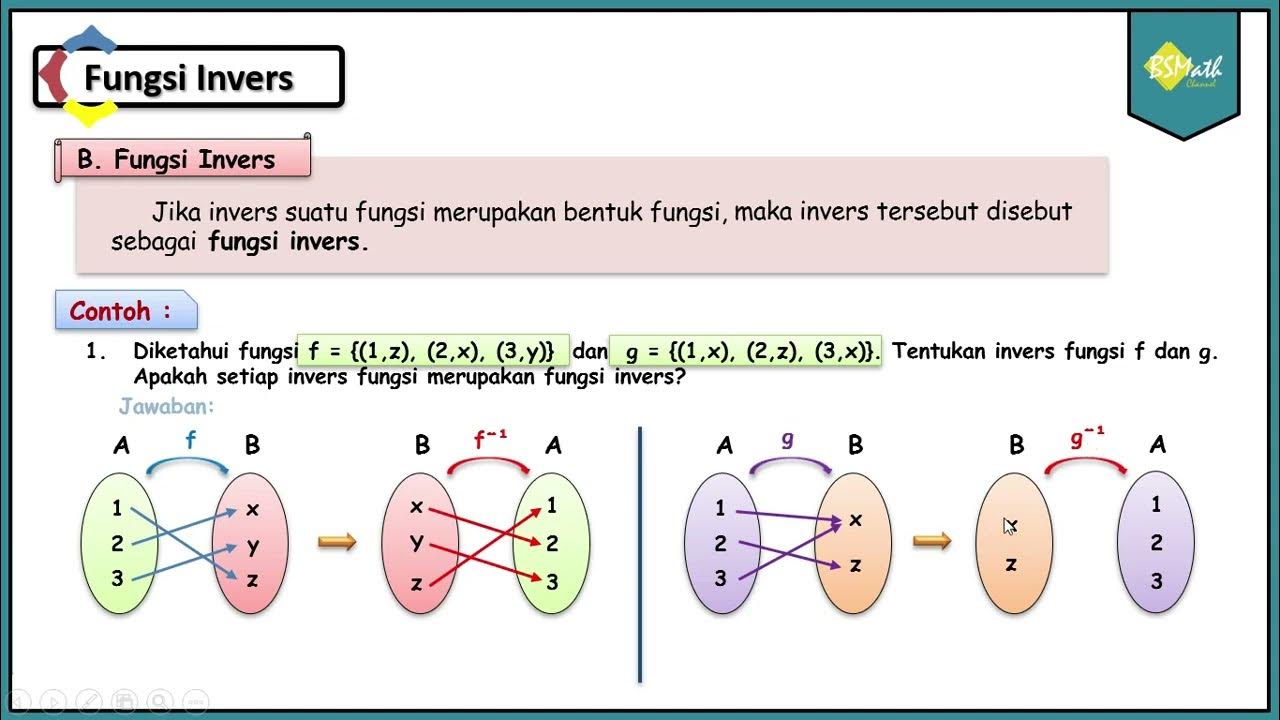
Fungsi Invers - Matematika SMA Kelas XI Kurikulum Merdeka

Korelasi Spearman - Matematika Wajib SMA Kelas XI Kurikulum Merdeka

Contoh Soal dan Pembahasan Tren Data, Korelasi dan Interpretasi Data Bivariat Diagram Pencar

Konsep Persamaan Linier Satu Variabel Hal 97-109 Bab 3 PLSV Kelas 8 Kurikulum Merdeka Belajar
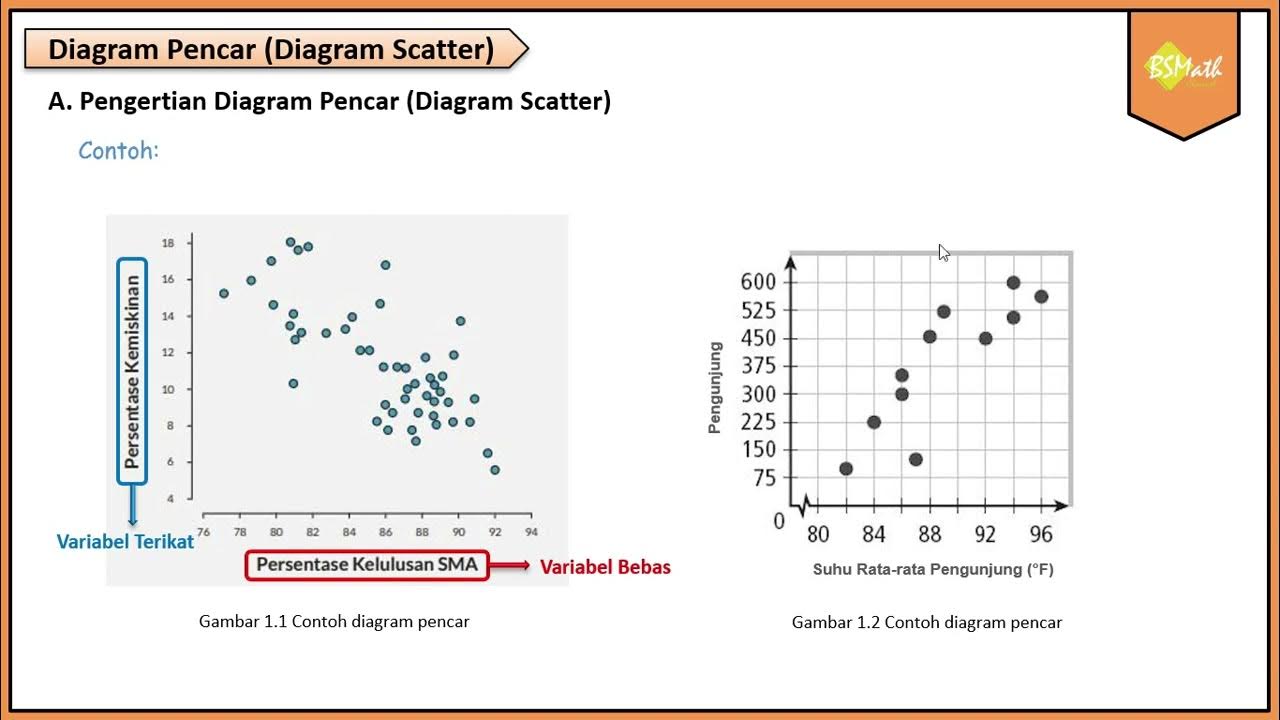
Pengertian Diagram Pencar - Matematika Wajib SMA Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)
