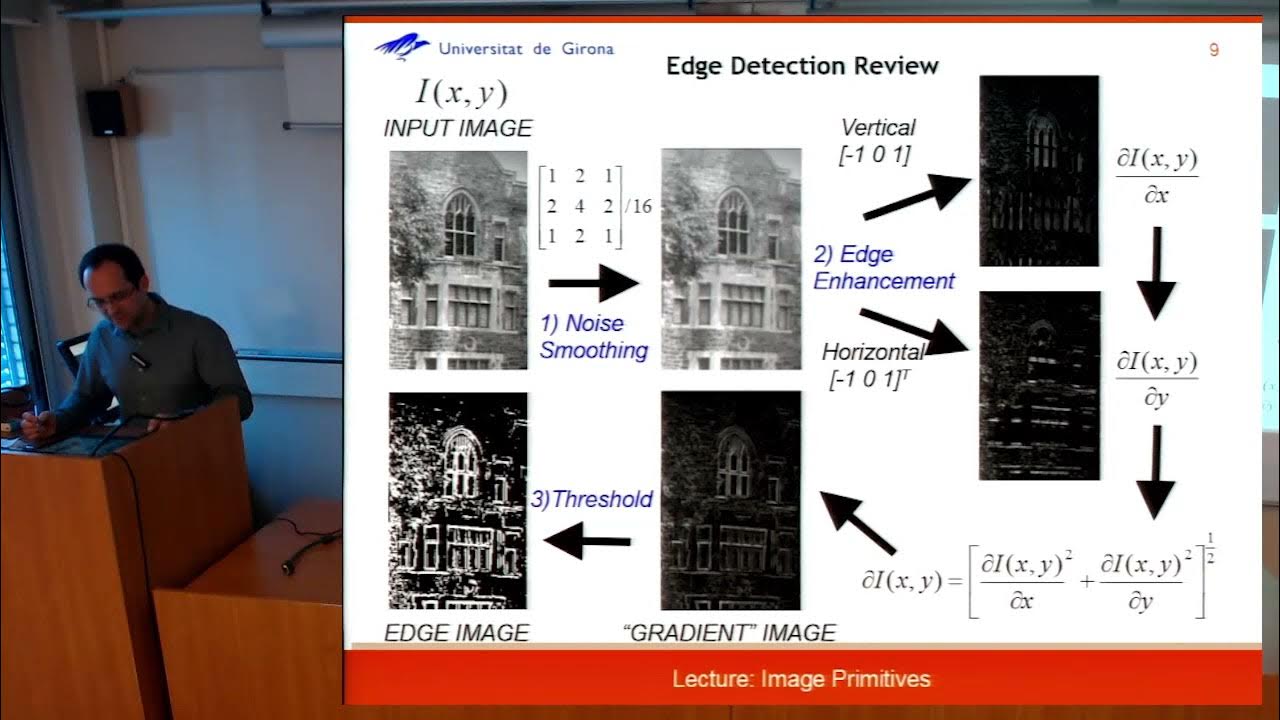
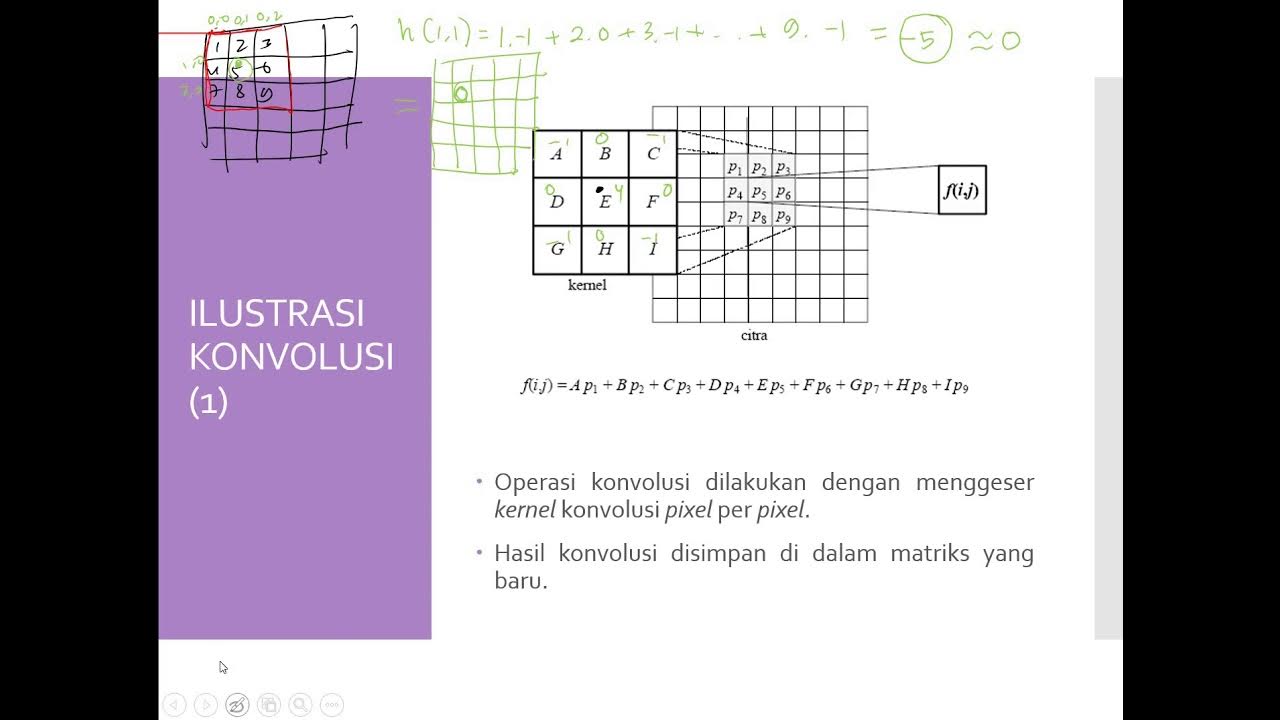
But what is a convolution?

Summary

This script explores the concept of convolution, a mathematical operation used in various fields like image processing and probability theory. It explains how convolution combines two lists or functions, such as multiplying polynomials or analyzing dice probabilities, to yield new insights. The video also delves into the practical application of convolution in blurring images and detecting edges. Furthermore, it introduces a faster algorithm for computing convolutions using the Fast Fourier Transform (FFT), which is more efficient than traditional methods, especially for large datasets.

Takeaways

• 🔢 Convolution is a mathematical operation that combines two lists of numbers or functions to produce a new list or function. It's different from simple addition or multiplication.
• 🎲 The concept is introduced through the example of rolling dice to illustrate how the sums can be visualized and calculated using convolution.
• 📊 Convolution is widely used in various fields such as image processing, probability theory, and solving differential equations, including in the context of polynomial multiplication.
• 💡 The script explains that convolution can be visualized by aligning one list with a flipped version of the other and calculating the sum of products at different offsets.
• 🎛️ In probability, convolution helps calculate the probability of various outcomes when dealing with non-uniform distributions, like weighted dice.
• 🖼️ In image processing, convolution is used for effects like blurring, edge detection, and sharpening by applying different 'kernels' or grids of values over the image.
• 📉 The script discusses how a moving average can be seen as a type of convolution, smoothing out data by averaging it within a sliding window.
• 🔄 The output length of a convolution is typically longer than the original lists, but in computer science, it can be truncated to match the original size.
• 🌀 The Fast Fourier Transform (FFT) algorithm is highlighted as a way to compute convolutions much more efficiently (O(n log n) instead of O(n²)) by leveraging the properties of polynomial multiplication.
• 🧮 An interesting connection is made to the idea that standard integer multiplication can also be viewed as a form of convolution, hinting at the possibility of more efficient multiplication algorithms for very large numbers.

Q & A

What are the three basic ways to combine two lists of numbers?

The three basic ways to combine two lists of numbers are by adding them term by term, multiplying them term by term, and using a convolution, which is less commonly discussed but very fundamental.

How is convolution different from addition and multiplication of lists?

Convolution is different from addition and multiplication of lists because it involves flipping one of the lists, aligning them at various offset values, taking pairwise products, and then summing them up, which creates a genuinely new sequence rather than just combining existing values.

In what contexts are convolutions commonly used?

Convolution is ubiquitous in image processing, a core construct in probability theory, frequently used in solving differential equations, and is also seen in polynomial multiplication.

How does the concept of convolution relate to rolling dice and calculating probabilities?

Convolution relates to rolling dice and calculating probabilities by visualizing the outcomes on a grid where diagonals represent constant sums, allowing for easy counting of combinations that result in a given sum.

What is the significance of the normal distribution in the context of probability as explained in the script?

The normal distribution is significant in probability because it naturally aligns with the process of convolution, which is a fundamental way to calculate probabilities when dealing with non-uniform probabilities across different outcomes.

How does the script explain the concept of convolution in the context of image processing?

The script explains convolution in image processing by using the example of blurring an image. It demonstrates how a grid of values (kernel) is used to multiply and sum pixel values, creating a smoothed or blurred version of the original image.

What is a kernel in the context of image processing?

In image processing, a kernel is a small grid of values that is used to apply effects to an image through convolution. Different kernels can be used for various effects like blurring, edge detection, or sharpening.

How does the script connect the concept of convolution to polynomial multiplication?

The script connects convolution to polynomial multiplication by showing that the process of creating a multiplication table for polynomials and summing along diagonals is equivalent to a convolution operation, which helps in expanding and combining polynomial terms efficiently.

What is the fast Fourier transform (FFT) and how does it relate to computing convolutions?

The fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform and its inverse very efficiently. It relates to computing convolutions by allowing the conversion of convolution operations into multiplications in the frequency domain, which can be computed much faster, especially for large lists.

How does the script suggest that the concept of convolution can be used to multiply large integers more efficiently?

The script suggests that by treating large integers as coefficients of polynomials, sampling them at roots of unity, and using the FFT algorithm, it's possible to multiply the integers more efficiently with an algorithm that requires O(n log n) operations instead of the traditional O(n^2).

Outlines

00:00

🔢 Combining Lists and Functions: An Introduction to Convolution

The paragraph introduces the concept of combining two lists or functions in various ways, such as addition and multiplication, and then delves into a less commonly discussed method known as convolution. Convolution is a fundamental operation in many fields, including image processing, probability theory, and differential equations. The paragraph uses the example of multiplying polynomials to illustrate convolution and sets the stage for a deeper exploration of the topic in the video. It also hints at the connection between convolution and normal distributions in probability without going into detail, promising a more comprehensive explanation in the video.

05:05

🎲 Convolving Dice Rolls: Understanding Convolution Through Probability

This paragraph uses the example of rolling dice to explain the concept of convolution in a probabilistic context. It describes how the sum of outcomes from two dice can be visualized and calculated through a grid arrangement, where diagonals represent constant sums. The concept is then extended to non-uniform dice, where the probabilities of each face are different, requiring a multiplication of probabilities for each pair of outcomes that sum to a particular value. The paragraph introduces the formal definition of convolution as a process of flipping one list, aligning it at different offsets, multiplying pairwise products, and summing them to get a new sequence of values.

10:06

📊 Convolution in Image Processing: Blurring and Edge Detection

The paragraph explores the application of convolution in image processing, specifically in blurring and edge detection. It describes how a grid of values, or kernel, is used to multiply and sum pixel values in an image to achieve a blurring effect. The paragraph contrasts different types of kernels, from uniform grids that produce a basic blur to Gaussian distributions that simulate an out-of-focus effect. It also demonstrates how altering the kernel can be used for edge detection by highlighting variations in pixel values. The concept of kernels and their impact on image processing is central to this section, showcasing the versatility of convolution in visual effects.

15:08

🧮 Fast Convolution Algorithms: The Power of FFT

This paragraph discusses the computational efficiency of convolution operations, particularly in the context of large data sets. It contrasts the direct computation of convolution, which is O(n^2), with the use of the Fast Fourier Transform (FFT) algorithm, which reduces the complexity to O(n log n). The paragraph explains how the FFT algorithm leverages the redundancy in the system of equations generated by evaluating polynomials at roots of unity, thus enabling a much faster computation. It also touches on the broader implications of this algorithm for various applications, including probability distributions and image processing, and suggests that the concept of convolutions appearing in different areas of math can lead to powerful and efficient algorithms.

20:11

🔍 Convolution and Polynomial Multiplication: A Deeper Dive

The final paragraph ties together the concept of convolution with polynomial multiplication, explaining that the process of expanding and combining like terms in polynomial multiplication is equivalent to convolution. It introduces the idea that instead of directly computing the convolution of two lists, one can sample the polynomials at specific points, multiply the samples, and then solve a system of equations to recover the coefficients. The paragraph highlights the potential for a more efficient algorithm for polynomial multiplication using this approach, especially when the numbers involved are very large. It concludes by suggesting that the connection between convolution and multiplication in various mathematical contexts can lead to faster algorithms and deeper insights.

Keywords

💡Convolution

Convolution is a mathematical operation that combines two functions or lists of numbers to produce a third function or list that represents the amount of overlap between the two as one is shifted over the other. In the video, convolution is central to understanding various applications such as image processing, probability distributions, and solving differential equations. The script uses the example of rolling dice to illustrate how convolution can be used to calculate probabilities of different sums, highlighting its fundamental role in combining and analyzing data sets.

💡Probability Distributions

A probability distribution is a statistical description of the likelihood of a random variable taking on each of a set of possible values. In the video, the concept is used to explain how convolution can be applied to calculate the likelihood of different outcomes when rolling dice with non-uniform probabilities. This demonstrates how convolution can be used to model and predict outcomes in probabilistic scenarios.

💡Image Processing

Image processing refers to any form of signal processing for which the input is an image, such as a photograph or video frame, and the output need not be an image. The video discusses how convolution is used in image processing to perform operations like blurring and edge detection. The script describes how applying a convolution with a specific kernel can blur an image, while choosing a different kernel can detect edges, showcasing convolution's versatility in manipulating visual data.

💡Polynomials

A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation. The video script uses polynomials to explain the connection between polynomial multiplication and convolution. It illustrates that multiplying two polynomials can be viewed as a convolution operation on their coefficients, which is a key insight that leads to more efficient computational methods.

💡Kernel

In the context of the video, a kernel is a small matrix used in image processing to perform various operations like blurring or edge detection through convolution. The script explains how different kernels can be used to achieve different effects on an image, such as a kernel with equal values for averaging (blurring) or a Gaussian kernel for a more realistic blur that mimics out-of-focus photography.

💡Fourier Transform

The Fourier Transform is a mathematical technique that decomposes a function into a set of frequencies. In the video, the script introduces the concept of the discrete Fourier transform (DFT) as part of the explanation for the fast Fourier transform (FFT) algorithm, which is used to compute convolutions more efficiently. The Fourier Transform is key to understanding how the FFT algorithm can reduce the computational complexity of convolutions from O(n^2) to O(n log n).

💡Fast Fourier Transform (FFT)

The Fast Fourier Transform (FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse. The video script highlights the FFT as a crucial tool in efficiently computing convolutions, especially for large data sets. By transforming the data into the frequency domain, the FFT allows for the multiplication of two data sets' spectra and then transforming back to the time domain to obtain the convolved output, all in a fraction of the time it would take with a direct convolution approach.

💡Discrete Case

The discrete case refers to scenarios where data is represented by a finite number of discrete points or samples. In the video, the script focuses on the discrete case of convolution, which is relevant to digital signal processing and digital image processing. The discussion of discrete convolution helps to build an understanding of the algorithmic and computational aspects of the operation, which is essential for practical applications in computer science and engineering.

💡Continuous Case

The continuous case, in contrast to the discrete case, involves data that can take on any value within a continuum. The video script mentions that the continuous case will be discussed in a separate part, focusing on probability distributions. This distinction is important for understanding the different mathematical treatments and applications of convolution in various fields, such as differential equations and continuous signal processing.

💡Algorithm

An algorithm is a set of rules or steps used to solve a problem or perform a computation. The video script discusses various algorithms related to convolution, including the direct computation of convolution and the more efficient FFT-based approach. Understanding these algorithms is crucial for optimizing the performance of operations that involve convolution, such as in image processing or probability theory.

Highlights

Exploration of combining two lists or functions through addition and multiplication, introducing convolution as a fundamental but less commonly discussed method.

Convolution's widespread applications in image processing, probability theory, and solving differential equations.

The convolution process as a new operation for combining lists or functions, distinct from simple addition or multiplication.

Visual explanation of convolution as a blending process, particularly in the context of polynomial multiplication.

Detailed discussion on the discrete case of convolution, emphasizing its importance in computational algorithms.

Introduction of a clever algorithm for computing convolutions, setting the stage for exploring continuous cases in a follow-up.

Use of probability and dice rolls as an accessible example to illustrate the concept of convolution.

Visualization of convolution through the alignment and multiplication of probability arrays, representing different outcomes.

Explanation of how convolution can be used to calculate probabilities with non-uniform dice, showcasing its adaptability.

The convolution of sequences as a method for generating new sequences through pairwise products and summation.

Demonstration of convolution with a simple numerical example, clarifying the process with step-by-step calculations.

Application of convolution in moving averages and data smoothing, providing a practical use case in statistics.

Image processing example using convolution to blur images, illustrating the technique's impact on visual data.

Discussion on the use of different kernels in image processing to achieve various effects, such as blurring and edge detection.

Introduction of the fast Fourier transform (FFT) as a method for efficiently computing convolutions, offering a significant computational advantage.

Comparison of computational efficiency between direct convolution and FFT-based methods, highlighting the后者's superior performance.

The polynomial multiplication example as a bridge between convolution and the fast Fourier transform, demonstrating the interconnectedness of mathematical concepts.

The potential for a faster algorithm for integer multiplication based on convolution, hinting at the broader implications of mathematical techniques.

Transcripts

Suppose I give you two different lists of numbers, or maybe two different functions,

and I ask you to think of all the ways you might combine those two lists to get

a new list of numbers, or combine the two functions to get a new function.

Maybe one simple way that comes to mind is to simply add them together term by term.

Likewise with the functions, you can add all the corresponding outputs.

In a similar vein, you could also multiply the two lists

term by term and do the same thing with the functions.

But there's another kind of combination just as fundamental as both of those,

but a lot less commonly discussed, known as a convolution.

But unlike the previous two cases, it's not something that's

merely inherited from an operation you can do to numbers.

It's something genuinely new for the context of lists of numbers or combining functions.

They show up all over the place, they are ubiquitous in image processing,

it's a core construct in the theory of probability,

they're used a lot in solving differential equations,

and one context where you've almost certainly seen it, if not by this name,

is multiplying two polynomials together.

As someone in the business of visual explanations, this is an especially great topic,

because the formulaic definition in isolation and without context can look kind of

intimidating, but if we take the time to really unpack what it's saying,

and before that actually motivate why you would want something like this,

it's an incredibly beautiful operation.

And I have to admit, I actually learned a little something

while putting together the visuals for this project.

In the case of convolving two different functions,

I was trying to think of different ways you might picture what that could mean,

and with one of them I had a little bit of an aha moment for why it is that

normal distributions play the role that they do in probability,

why it's such a natural shape for a function.

But I'm getting ahead of myself, there's a lot of setup for that one.

In this video, our primary focus is just going to be on the discrete case,

and in particular building up to a very unexpected but very clever algorithm for

computing these.

And I'll pull out the discussion for the continuous case into a second part.

It's very tempting to open up with the image processing examples,

since they're visually the most intriguing, but there are a couple bits of finickiness

that make the image processing case less representative of convolutions overall,

so instead let's kick things off with probability,

and in particular one of the simplest examples that I'm sure everyone here has

thought about at some point in their life, which is rolling a pair of dice and

figuring out the chances of seeing various different sums.

And you might say, not a problem, not a problem.

Each of your two dice has six different possible outcomes,

which gives us a total of 36 distinct possible pairs of outcomes,

and if we just look through them all we can count up how many pairs have a given sum.

And arranging all the pairs in a grid like this,

one pretty nice thing is that all of the pairs that have a constant sum are visible

along one of these different diagonals.

So simply counting how many exist on each of those diagonals

will tell you how likely you are to see a particular sum.

And I'd say, very good, very good, but can you think of

any other ways that you might visualize the same question?

Other images that can come to mind to think of

all the distinct pairs that have a given sum?

And maybe one of you raises your hand and says, yeah, I've got one.

Let's say you picture these two different sets of possibilities each in a row,

but you flip around that second row.

That way all of the different pairs which add up to seven line up vertically like this.

And if we slide that bottom row all the way to the right,

then the unique pair that adds up to two, the snake eyes, are the only ones that align,

and if I schlunk that over one unit to the right,

the pairs which align are the two different pairs that add up to three.

And in general, different offset values of this lower array,

which remember I had to flip around first, reveal all the distinct pairs that

have a given sum.

As far as probability questions go, this still isn't especially interesting because

all we're doing is counting how many outcomes there are in each of these categories.

But that is with the implicit assumption that there's

an equal chance for each of these faces to come up.

But what if I told you I have a special set of dice that's not uniform?

Maybe the blue die has its own set of numbers describing the probabilities for

each face coming up, and the red die has its own unique distinct set of numbers.

In that case, if you wanted to figure out, say,

the probability of seeing a 2, you would multiply the probability

that the blue die is a 1 times the probability that the red die is a 1.

And for the chances of seeing a 3, you look at the two distinct

pairs where that's possible, and again multiply the corresponding

probabilities and then add those two products together.

Similarly, the chances of seeing a 4 involves multiplying together

three different pairs of possibilities and adding them all together.

And in the spirit of setting up some formulas, let's name these top probabilities a 1,

a 2, a 3, and so on, and name the bottom ones b 1, b 2, b 3, and so on.

And in general, this process where we're taking two different arrays of numbers,

flipping the second one around, and then lining them up at various different

offset values, taking a bunch of pairwise products and adding them up,

that's one of the fundamental ways to think about what a convolution is.

So just to spell it out a little more exactly, through this process,

we just generated probabilities for seeing 2, 3, 4, on and on up to 12,

and we got them by mixing together one list of values, a, and another list of values, b.

In the lingo, we'd say the convolution of those two sequences gives us this new sequence,

the new sequence of 11 values, each of which looks like some sum of pairwise products.

If you prefer, another way you could think about the same operation is to first

create a table of all the pairwise products, and then add up along all these diagonals.

Again, that's a way of mixing together these two

sequences of numbers to get us a new sequence of 11 numbers.

It's the same operation as the sliding windows thought, just another perspective.

Putting a little notation to it, here's how you might see it written down.

The convolution of a and b, denoted with this little asterisk, is a new list,

and the nth element of that list looks like a sum,

and that sum goes over all different pairs of indices, i and j,

so that the sum of those indices is equal to n.

It's kind of a mouthful, but for example, if n was 6,

the pairs we're going over are 1 and 5, 2 and 4, 3 and 3, 4 and 2, 5 and 1,

all the different pairs that add up to 6.

But honestly, however you write it down, the notation is secondary in

importance to the visual you might hold in your head for the process.

Here, maybe it helps to do a super simple example,

where I might ask you what's the convolution of the list 1, 2, 3 with the list 4, 5, 6.

You might picture taking both of these lists, flipping around that second one,

and then starting with its lid all the way over to the left.

Then the pair of values which align are 1 and 4,

multiply them together, and that gives us our first term of our output.

Slide that bottom array one unit to the right,

the pairs which align are 1, 5 and 2 and 4, multiply those pairs,

add them together, and that gives us 13, the next entry in our output.

Slide things over once more, and we'll take 1 times 6 plus 2 times 5 plus 3 times 4,

which happens to be 28.

One more slide and we get 2 times 6 plus 3 times 5, and that gives us 27.

And finally the last term will look like 3 times 6.

If you'd like, you can pull up whatever your favorite programming

language is and your favorite library that includes various numerical operations,

and you can confirm I'm not lying to you.

If you take the convolution of 1, 2, 3 against 4,

5, 6, this is indeed the result that you'll get.

We've seen one case where this is a natural and desirable operation,

adding up to probability distributions, and another common example would be a

moving average.

Imagine you have some long list of numbers, and you take

another smaller list of numbers that all add up to 1.

In this case, I just have a little list of 5 values and they're all equal to 1 5th.

Then if we do this sliding window convolution process,

and kind of close our eyes and sweep under the rug what happens at

the very beginning of it, once our smaller list of values entirely

overlaps with the bigger one, think about what each term in this convolution really means.

At each iteration, what you're doing is multiplying each of the values

from your data by 1 5th and adding them all together,

which is to say you're taking an average of your data inside this little window.

Overall, the process gives you a smoothed out version of the original data,

and you could modify this starting with a different little list of numbers,

and as long as that little list all adds up to 1,

you can still interpret it as a moving average.

In the example shown here, that moving average

would be giving more weight towards the central value.

This also results in a smoothed out version of the data.

If you do kind of a two-dimensional analog of this,

it gives you a fun algorithm for blurring a given image.

And I should say the animations I'm about to show are modified from something

I originally made for part of a set of lectures I did with the Julia lab at

MIT for a certain open courseware class that included an image processing unit.

There we did a little bit more to dive into the code behind all of this,

so if you're curious, I'll leave you some links.

But focusing back on this blurring example, what's going on is I've got this

little 3x3 grid of values that's marching along our original image, and if we zoom in,

each one of those values is 1 9th, and what I'm doing at each iteration is

multiplying each of those values by the corresponding pixel that it sits on top of.

And of course in computer science, we think of colors as little vectors of three values,

representing the red, green, and blue components.

When I multiply all these little values by 1 9th and I add them together,

it gives us an average along each color channel,

and the corresponding pixel for the image on the right is defined to be that sum.

The overall effect, as we do this for every single pixel on the image,

is that each one kind of bleeds into all of its neighbors,

which gives us a blurrier version than the original.

In the lingo, we'd say that the image on the right is a

convolution of our original image with a little grid of values.

Or more technically, maybe I should say that it's the convolution

with a 180 degree rotated version of that little grid of values.

Not that it matters when the grid is symmetric,

but it's just worth keeping in mind that the definition of a convolution,

as inherited from the pure math context, should always invite you to think about

flipping around that second array.

If we modify this slightly, we can get a much more elegant

blurring effect by choosing a different grid of values.

In this case, I have a little 5x5 grid, but the distinction is not so much its size.

If we zoom in, we notice that the value in the middle

is a lot bigger than the value towards the edges.

And where this is coming from is they're all sampled from a bell curve,

known as a Gaussian distribution.

That way, when we multiply all of these values by the corresponding

pixel that they're sitting on top of, we're giving a lot more weight

to that central pixel, and much less towards the ones out at the edge.

And just as before, the corresponding pixel on the right is defined to be this sum.

As we do this process for every single pixel, it gives a blurring effect,

which much more authentically simulates the notion of putting your lens out of focus,

or something like that.

But blurring is far from the only thing that you can do with this idea.

For instance, take a look at this little grid of values,

which involves some positive numbers on the left,

and some negative numbers on the right, which I'll color with blue and red respectively.

Take a moment to see if you can predict and understand

what effect this will have on the final image.

So in this case, I'll just be thinking of the image as grayscale instead of colored,

so each of the pixels is just represented by one number instead of three.

And one thing worth noticing is that as we do this convolution,

it's possible to get negative values.

For example, at this point here, if we zoom in,

the left half of our little grid sits entirely on top of black pixels,

which would have a value of zero, but the right half of negative values all sit on

top of white pixels, which would have a value of one.

So when we multiply corresponding terms and add them together,

the results will be very negative.

And the way I'm displaying this with the image on the right

is to color negative values red and positive values blue.

Another thing to notice is that when you're on a patch that's all the same color,

everything goes to zero, since the sum of the values in our little grid is zero.

This is very different from the previous two examples where the sum of our little

grid was one, which let us interpret it as a moving average and hence a blur.

All in all, this little process basically detects wherever there's

variation in the pixel value as you move from left to right,

and so it gives you a kind of way to pick up on all the vertical edges from your image.

And similarly, if we rotated that grid around so that it varies as you move from

the top to the bottom, this will be picking up on all the horizontal edges,

which in the case of our little pie creature image does result in some pretty

demonic eyes.

This smaller grid, by the way, is often called a kernel,

and the beauty here is how just by choosing a different kernel,

you can get different image processing effects, not just blurring your edge detection,

but also things like sharpening.

For those of you who have heard of a convolutional neural network,

the idea there is to use data to figure out what the kernels should be in

the first place, as determined by whatever the neural network wants to detect.

Another thing I should maybe bring up is the length of the output.

For something like the moving average example,

you might only want to think about the terms when both of the windows

fully align with each other.

Or in the image processing example, maybe you want

the final output to have the same size as the original.

Now, convolutions as a pure math operation always produce an

array that's bigger than the two arrays that you started with,

at least assuming one of them doesn't have a length of one.

Just know that in certain computer science contexts,

you often want to deliberately truncate that output.

Another thing worth highlighting is that in the computer science context,

this notion of flipping around that kernel before you let it march across

the original often feels really weird and just uncalled for, but again,

note that that's what's inherited from the pure math context,

where like we saw with the probabilities, it's an incredibly natural thing to do.

And actually, I can show you one more pure math example where

even the programmers should care about this one,

because it opens the doors for a much faster algorithm to compute all of these.

To set up what I mean by faster here, let me go back and pull up some Python again,

and I'm going to create two different relatively big arrays.

Each one will have a hundred thousand random elements in it,

and I'm going to assess the runtime, of the convolve function from the NumPy library.

And in this case, it runs it for multiple different iterations, tries to find an average,

and it looks like, on this computer at least, it averages at 4.87 seconds.

By contrast, if I use a different function from the SciPy library called fftConvolve,

which is the same thing just implemented differently,

that only takes 4.3 milliseconds on average, so three orders of magnitude improvement.

And again, even though it flies under a different name,

it's giving the same output that the other convolve function does,

it's just doing something to go about it in a cleverer way.

Remember how with the probability example, I said another way you could

think about the convolution was to create this table of all the pairwise products,

and then add up those pairwise products along the diagonals.

There's of course nothing specific to probability.

Any time you're convolving two different lists of numbers,

you can think about it this way.

Create this kind of multiplication table with all pairwise products,

and then each sum along the diagonal corresponds to one of your final outputs.

One context where this view is especially natural

is when you multiply together two polynomials.

For example, let me take the little grid we already have and replace the top terms

with 1, 2x, and 3x squared, and replace the other terms with 4, 5x, and 6x squared.

Now, think about what it means when we're creating all of

these different pairwise products between the two lists.

What you're doing is essentially expanding out the full product of

the two polynomials I have written down, and then when you add up along the diagonal,

that corresponds to collecting all like terms.

Which is pretty neat.

Expanding a polynomial and collecting like terms

is exactly the same process as a convolution.

But this allows us to do something that's pretty cool,

because think about what we're saying here.

We're saying if you take two different functions and you multiply them together,

which is a simple pointwise operation, that's the same thing as if you had

first extracted the coefficients from each one of those, assuming they're polynomials,

and then taken a convolution of those two lists of coefficients.

What makes that so interesting is that convolutions feel,

in principle, a lot more complicated than simple multiplication.

And I don't just mean conceptually they're harder to think about.

I mean, computationally, it requires more steps to perform a convolution

than it does to perform a pointwise product of two different lists.

For example, let's say I gave you two really big polynomials,

say each one with a hundred different coefficients.

Then if the way you multiply them was to expand out this product,

you know, filling in this entire 100 by 100 grid of pairwise products,

that would require you to perform 10,000 different products.

And then, when you're collecting all the like terms along the diagonals,

that's another set of around 10,000 operations.

More generally, in the lingo, we'd say the algorithm is O of n squared,

meaning for two lists of size n, the way that the number of

operations scales is in proportion to the square of n.

On the other hand, if I think of two polynomials in terms of their outputs, for example,

sampling their values at some handful of inputs,

then multiplying them only requires as many operations as the number of samples,

since again, it's a pointwise operation.

And with polynomials, you only need finitely many

samples to be able to recover the coefficients.

For example, two outputs are enough to uniquely specify a linear polynomial,

three outputs would be enough to uniquely specify a quadratic polynomial,

and in general, if you know n distinct outputs,

that's enough to uniquely specify a polynomial that has n different coefficients.

Or, if you prefer, we could phrase this in the language of systems of equations.

Imagine I tell you I have some polynomial, but I don't tell you what the coefficients are.

Those are a mystery to you.

In our example, you might think of this as the product that we're trying to figure out.

And then, suppose I say, I'll just tell you what the outputs of this polynomial

would be if you inputted various different inputs, like 0, 1, 2, 3, on and on,

and I give you enough so that you have as many equations as you have unknowns.

It even happens to be a linear system of equations, so that's nice,

and in principle, at least, this should be enough to recover the coefficients.

So the rough algorithm outline then would be, whenever you want to convolve two lists

of numbers, you treat them like they're coefficients of two polynomials,

you sample those polynomials at enough outputs, multiply those samples point-wise,

and then solve this system to recover the coefficients as a sneaky backdoor way to find

the convolution.

And, as I've stated it so far, at least, some of you could rightfully complain, grant,

that is an idiotic plan, because, for one thing,

just calculating all these samples for one of the polynomials we know already takes

on the order of n-squared operations.

Not to mention, solving that system is certainly going to be

computationally as difficult as just doing the convolution in the first place.

So, like, sure, we have this connection between multiplication and convolutions,

but all of the complexity happens in translating from one viewpoint to the other.

But there is a trick, and those of you who know about Fourier

transforms and the FFT algorithm might see where this is going.

If you're unfamiliar with those topics, what I'm

about to say might seem completely out of the blue.

Just know that there are certain paths you could have

walked in math that make this more of an expected step.

Basically, the idea is that we have a freedom of choice here.

If instead of evaluating at some arbitrary set of inputs, like 0, 1, 2, 3,

on and on, you choose to evaluate on a very specially selected set of complex numbers,

specifically the ones that sit evenly spaced on the unit circle,

what are known as the roots of unity, this gives us a friendlier system.

The basic idea is that by finding a number where taking its powers falls into

this cycling pattern, it means that the system we generate is going to have a

lot of redundancy in the different terms that you're calculating,

and by being clever about how you leverage that redundancy,

you can save yourself a lot of work.

This set of outputs that I've written has a special name.

It's called the discrete Fourier transform of the coefficients,

and if you want to learn more, I actually did another lecture for that same Julia MIT

class all about discrete Fourier transforms, and there's also a really excellent video on

the channel Reducible talking about the fast Fourier transform,

which is an algorithm for computing these more quickly.

Also Veritasium recently did a really good video on FFTs, so you've got lots of options.

And that fast algorithm really is the point for us.

Again, because of all this redundancy, there exists a method to go from

the coefficients to all of these outputs, where instead of doing on

the order of n squared operations, you do on the order of n times the

log of n operations, which is much much better as you scale to big lists.

And, importantly, this FFT algorithm goes both ways.

It also lets you go from the outputs to the coefficients.

So, bringing it all together, let's look back at our algorithm outline.

Now we can say, whenever you're given two long lists of numbers,

and you want to take their convolution, first compute the fast Fourier transform of

each one of them, which, in the back of your mind,

you can just think of as treating them like they're the coefficients of a polynomial,

and evaluating it at a very specially selected set of points.

Then, multiply together the two results that you just got, point-wise,

which is nice and fast, and then do an inverse fast Fourier transform,

and what that gives you is the sneaky backdoor way to compute the convolution that

we were looking for.

But this time, it only involves O of n log n operations.

That's really cool to me.

This very specific context where convolutions show up,

multiplying two polynomials, opens the doors for an algorithm

that's relevant everywhere else where convolutions might come up.

If you want to add probability distributions, do some large image processing,

whatever it might be, and I just think that's such a good example of why you should be

excited when you see some operation or concept in math show up in a lot of seemingly

unrelated areas.

If you want a little homework, here's something that's fun to think about.

Explain why when you multiply two different numbers,

just ordinary multiplication the way we all learn in elementary school,

what you're doing is basically a convolution between the digits of those numbers.

There's some added steps with carries and the like, but the core step is a convolution.

In light of the existence of a fast algorithm,

what that means is if you have two very large integers,

then there exists a way to find their product that's faster than the method we learn

in elementary school, that instead of requiring O of n squared operations,

only requires O of n log n, which doesn't even feel like it should be possible.

The catch is that before this is actually useful in practice,

your numbers would have to be absolutely monstrous.

But still, it's cool that such an algorithm exists.

And next up, we'll turn our attention to the continuous

case with a special focus on probability distributions.