Identifying Sets of Real Numbers

Summary

This educational script delves into the classification of real numbers, distinguishing between rational and irrational numbers. It outlines the hierarchy starting from natural numbers (N), moving up to whole numbers (W), integers (Z), and then rational numbers (Q), which include integers, whole numbers, and fractions like 2/3. Rational numbers are characterized by terminating or repeating decimals, while irrational numbers, such as the square root of 5 and pi, have non-terminating, non-repeating decimal expansions. The script uses examples and a Venn diagram to clarify these concepts, aiming to help students understand the properties and relationships among different sets of real numbers.

Takeaways

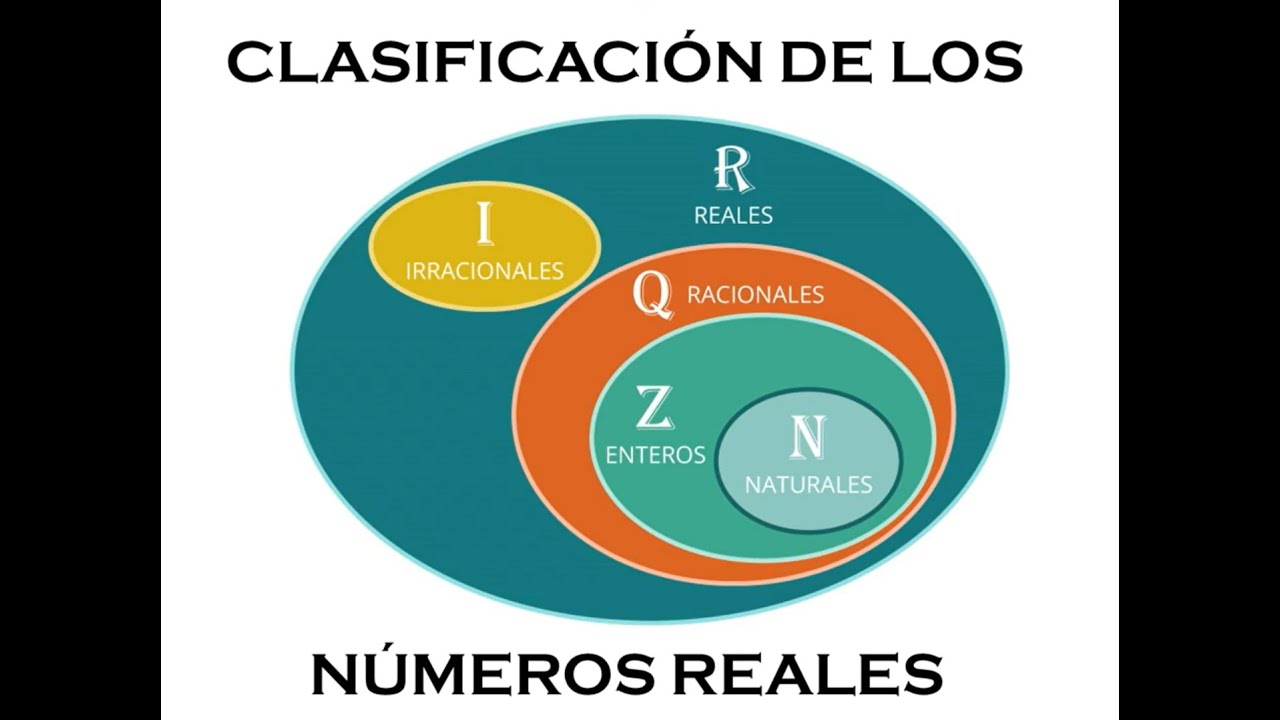
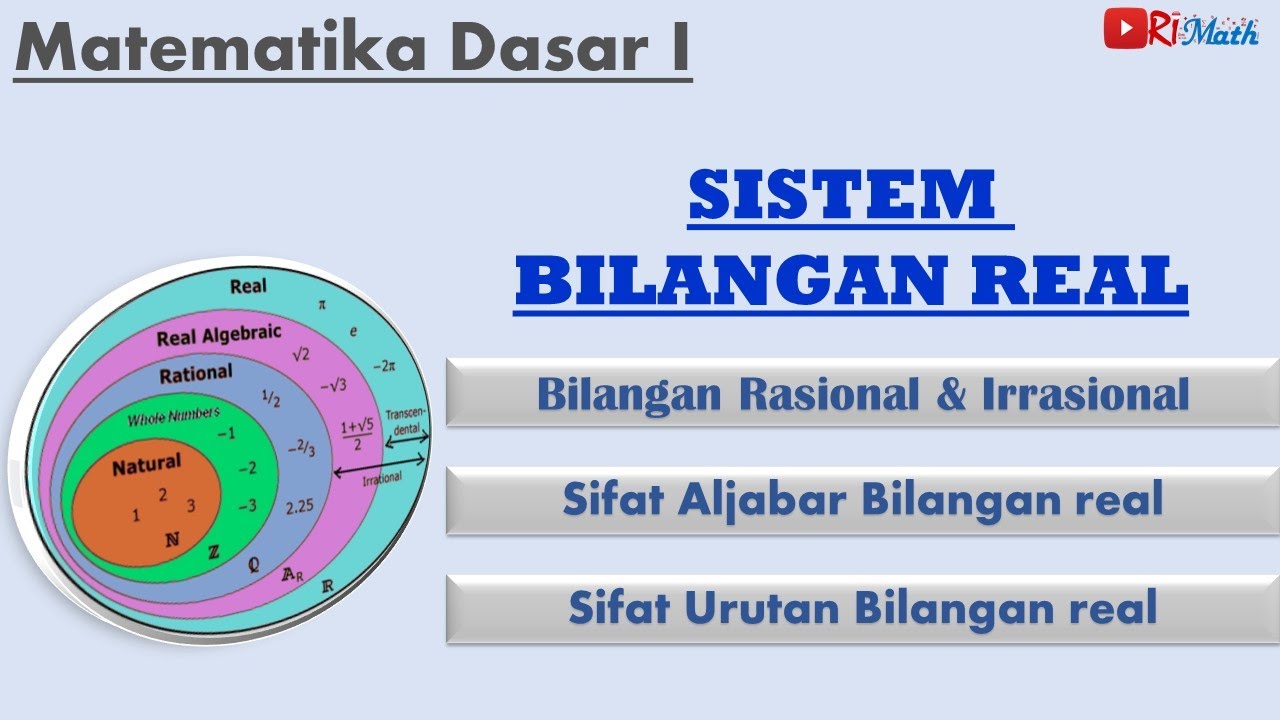
• 📏 Real numbers, denoted by the capital R, are all the numbers that can be represented on the number line, and they are either rational or irrational.
• 🔢 Natural numbers, represented by the capital N, are the set of counting numbers starting from 1, 2, 3, and so on.
• 📚 Whole numbers, denoted by the capital W, include all natural numbers and the number 0.
• ⏹ Integers, indicated by the capital Z, encompass all natural numbers, their negative counterparts, and 0.
• 🔑 Rational numbers, part of the set Q, can be expressed as a fraction a/b where a and b are integers, and b ≠ 0. They include integers, whole numbers, and natural numbers.
• 🔄 Rational numbers in decimal form either terminate or repeat, such as 0.4 and 0.3.
• 🌀 Irrational numbers, in contrast, are non-terminating and non-repeating decimals, like the square root of 5 and pi.
• 🔢 The number 0 is a whole number, an integer, a rational number, and a real number.
• 📈 The fraction 2/3 is rational and real, as it can be represented as a repeating decimal .666...
• 🛑 The square root of 8 is irrational and real, as it is a non-terminating, non-repeating decimal.
• 🔄 Negative square root of 36 simplifies to -6, which is an integer, rational, and real.
• 📏 Pi is an irrational number, as it is a non-terminating, non-repeating decimal, and it is also a real number.

Q & A

What are real numbers identified by?

Real numbers are identified by the capital letter R and are numbers that can be represented on the number line.

What are the two main categories of real numbers?

The two main categories of real numbers are rational numbers and irrational numbers.

What are natural numbers and how are they represented?

Natural numbers are the counting numbers starting from 1, 2, 3, and so on, and they are represented by the capital letter N.

What is the difference between natural numbers and whole numbers?

Whole numbers include all natural numbers and also the number 0, whereas natural numbers start from 1 and do not include 0.

How are integers different from natural numbers?

Integers include all natural numbers, the number 0, and negative numbers, while natural numbers only include the positive counting numbers starting from 1.

What is the form in which rational numbers can be expressed?

Rational numbers can be expressed in the form of 'A' divided by 'B', where 'A' and 'B' are integers and 'B' is not equal to 0.

How can you identify a rational number in decimal form?

A rational number in decimal form either terminates or repeats.

What is the difference between a terminating decimal and a repeating decimal?

A terminating decimal is a decimal that has a finite number of digits after the decimal point, while a repeating decimal has one or more digits that repeat infinitely.

Why is the square root of 5 considered an irrational number?

The square root of 5 is considered irrational because it is a non-terminating, non-repeating decimal, meaning it does not have a pattern that repeats indefinitely.

What is the significance of converting fractions to decimal form to determine if they are rational?

Converting fractions to decimal form helps in determining if they are rational by checking if the decimal terminates or repeats, which is a characteristic of rational numbers.

How does the number pi demonstrate the properties of irrational numbers?

Pi demonstrates the properties of irrational numbers because it is a non-terminating, non-repeating decimal with no repeating pattern.

Why does the negative square root of 36 not belong to the set of irrational numbers?

The negative square root of 36 simplifies to -6, which is an integer and therefore a rational number, not an irrational number.

How can a tree diagram help in understanding the hierarchy of different sets of numbers?

A tree diagram visually represents the hierarchy and relationships between different sets of numbers, such as real, rational, irrational, integers, whole numbers, and natural numbers, making it easier to understand their inclusion and distinctions.