Bilangan Kompleks • Part 1: Klasifikasi Bilangan

Summary

This video on the Jendela Sains channel explores the classification of numbers, focusing on complex numbers, real numbers, rational and irrational numbers, integers, and prime and composite numbers. The content provides clear definitions and examples of different number types, such as real numbers (R), imaginary numbers, rational numbers (fractions and integers), and irrational numbers (like π and √2). The video also highlights the distinctions between prime and composite numbers and gives viewers a thorough understanding of these mathematical concepts through detailed explanations and classifications.

Takeaways

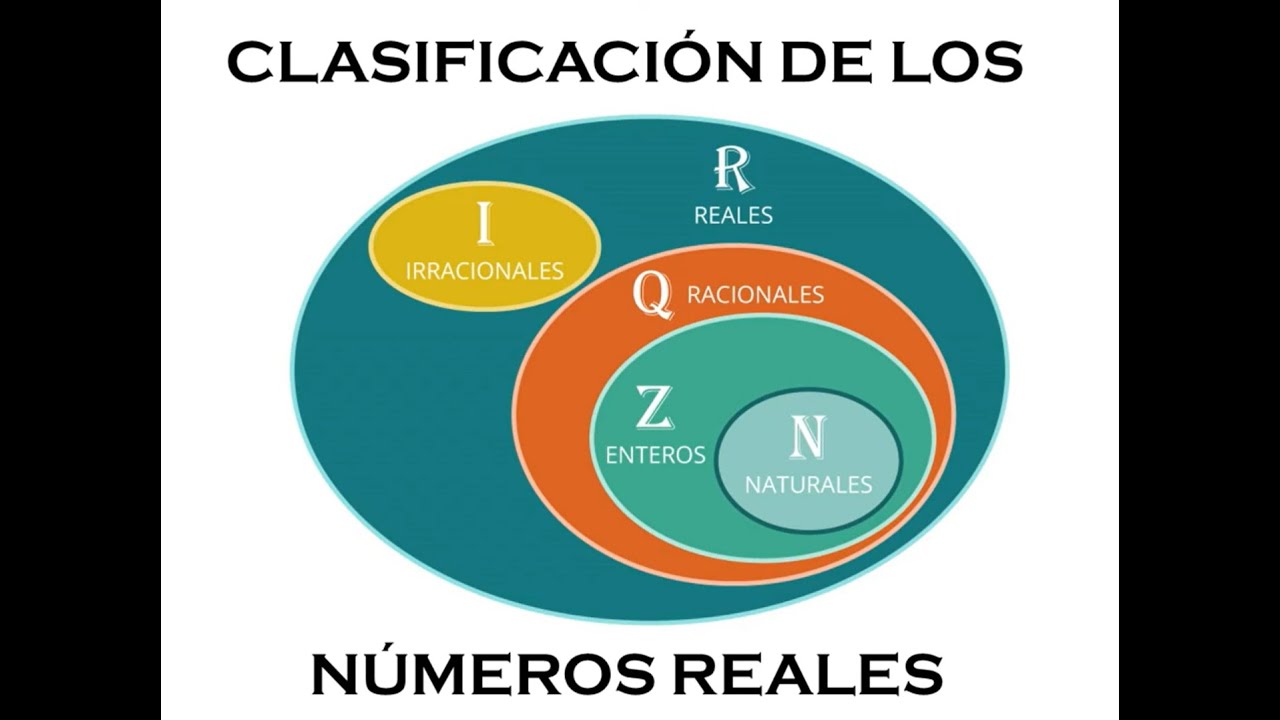
• 😀 Real numbers are numbers that can be clearly defined and placed on a number line.
• 😀 Imaginary numbers cannot be represented on a number line and include values like the square root of negative numbers.
• 😀 Rational numbers can be expressed as a fraction of two integers, such as 1/3 or -2.4.
• 😀 Irrational numbers cannot be expressed as simple fractions and include numbers like √2, π, and e.
• 😀 Integers are whole numbers, both positive and negative, including zero (e.g., -3, 0, 5).
• 😀 Fractions are numbers that can be expressed as a ratio of two integers (e.g., 1/3, -2.4).
• 😀 Negative integers are integers smaller than zero, while whole numbers are non-negative integers starting from zero.
• 😀 Natural numbers are positive integers starting from 1 (e.g., 1, 2, 3).
• 😀 Prime numbers are natural numbers greater than 1 with only two divisors: 1 and the number itself (e.g., 2, 3, 5).
• 😀 Composite numbers are natural numbers greater than 1 with divisors other than 1 and the number itself (e.g., 4, 6, 8).
• 😀 The number 1 is neither a prime nor a composite number but stands alone as a unique integer.

Q & A

What is the main topic of the video?

The main topic of the video is the classification of numbers, specifically focusing on complex numbers and their types, including real numbers, imaginary numbers, rational and irrational numbers, integers, fractions, and prime numbers.

What are the two main categories into which all numbers can be classified?

Numbers can be classified into two main categories: real numbers and imaginary numbers.

What is a real number, and how is it represented on the number line?

A real number is any number that can be represented on the number line. It includes both positive and negative numbers, as well as fractions and decimals. Real numbers can be exactly located on the number line.

Can all numbers be considered real numbers?

No, not all numbers are real numbers. Imaginary numbers, such as the square root of negative numbers, cannot be represented on the number line and are not real numbers.

What is an imaginary number?

An imaginary number is a number whose value is not clearly defined on the number line, typically involving the square root of negative numbers, such as √-1 or √-2.

How do you differentiate between rational and irrational numbers?

Rational numbers can be expressed as the ratio of two integers (a/b), where b is not zero. Irrational numbers, on the other hand, cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.

What are some examples of rational numbers?

Examples of rational numbers include integers like 2, -3, and 5, as well as fractions like 1/2, -3/4, and 0.25, which can be expressed as ratios of integers.

What makes π (Pi) and e irrational numbers?

Both π and e are irrational because their decimal expansions are non-repeating and non-terminating, and they cannot be expressed as exact fractions of two integers.

What is the difference between an integer and a fraction?

An integer is a whole number that does not have a fractional or decimal component, such as -3, 0, or 5. A fraction represents a part of a whole and is expressed as the ratio of two integers, like 1/3 or -2/5.

What is the classification of the number 1 in terms of prime, composite, and other types of numbers?

The number 1 is neither a prime nor a composite number. It only has one factor, which is itself, and thus stands as a unique category.