MATHEMATICS IN NATURE PROVES INTELLIGENT DESIGN
Summary
TLDRThis video explores the fundamentals of Chaos Theory through a simple equation that generates seemingly random numbers. Using a computer, the equation is iterated many times, revealing an emerging pattern. This self-similarity is a key concept of fractals, where zooming in on a part of the pattern reveals identical structures. The video uses the example of a fern leaf to demonstrate how nature exhibits self-similarity in its branching patterns. It also highlights the beauty and symmetry found in the natural world, which often manifests in forms like branches, spirals, and layers.
Takeaways
- 😀 Chaos Theory is based on a simple equation that appears random at first but reveals order with enough iterations.
- 😀 Microprocessors were key to discovering the patterns hidden within the equation of Chaos Theory.
- 😀 By iterating the equation many times, random numbers give rise to recognizable patterns, especially with the help of computers.
- 😀 After several iterations of a particular equation, a fern-like shape emerges, demonstrating how order forms out of apparent chaos.
- 😀 Self-similarity is an important concept in Chaos Theory: a pattern repeats itself at different scales, even as you zoom in.
- 😀 The pattern of self-similarity can be seen in nature, such as in the structure of fern leaves.
- 😀 A fern leaf, when viewed at multiple levels of magnification, displays the same branching pattern at each level.
- 😀 Self-similarity, or fractals, is a key concept in Chaos Theory, showing how complex patterns emerge from simple rules.
- 😀 Nature often presents forms and symmetries like branches, spirals, and layers, which are aesthetically pleasing and mathematically predictable.
- 😀 Radial symmetry and bilateral symmetry are examples of the forms found in nature, contributing to the beauty and structure of living organisms.
Q & A
What is the main concept introduced at the beginning of the script?
-The script introduces Chaos Theory, explaining that it is based on a simple equation that produces seemingly random results but reveals order when iterated many times using a computer.
Why was the discovery of the secrets behind the equation delayed until the advent of the microprocessor?
-Because the equation requires performing hundreds of thousands or millions of iterations, which was not feasible without the computational power provided by microprocessors.
How does the equation in Chaos Theory operate?
-The equation starts with an initial value for a variable, calculates a result, then feeds that result back into the equation repeatedly, generating a sequence of values that initially seem random.
What happens visually when the equation is iterated multiple times?
-At first, the results appear random, like scattered points. However, as the number of iterations increases, a clear pattern begins to emerge, forming recognizable structures such as a fern leaf.
What natural shape is formed by repeatedly applying the equation described in the script?
-A fern leaf shape emerges after several thousand iterations of the equation.
What is meant by 'self-similarity' in the context of Chaos Theory?
-Self-similarity means that parts of a structure resemble the whole structure, so if you zoom in on a smaller section, it looks similar to the larger overall pattern.
What subset of Chaos Theory deals with self-similar structures?
-The subset is called fractals, which are mathematical patterns that exhibit self-similarity across different scales.
How does the fern leaf in nature demonstrate self-similarity?
-Each branch of the fern resembles the full fern, and each smaller leaf on the branch also repeats the same pattern, showing multiple levels of self-similarity.
What three forms are commonly observed in nature according to the script?
-Branches, spirals, and layers are the three forms commonly observed in both the physical and natural worlds.
What types of symmetry contribute to the beauty of natural forms?
-Radial symmetry and bilateral symmetry contribute to the visual beauty and harmony of natural structures.
What is the overall message of the script regarding patterns in nature?
-The script emphasizes that natural forms, though they may appear chaotic, often follow predictable patterns of form, symmetry, and self-similarity, illustrating the underlying order in nature.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Simple Random Sampling

Ian Stewart's Nature's Numbers: Chapter 1 - The Natural Order
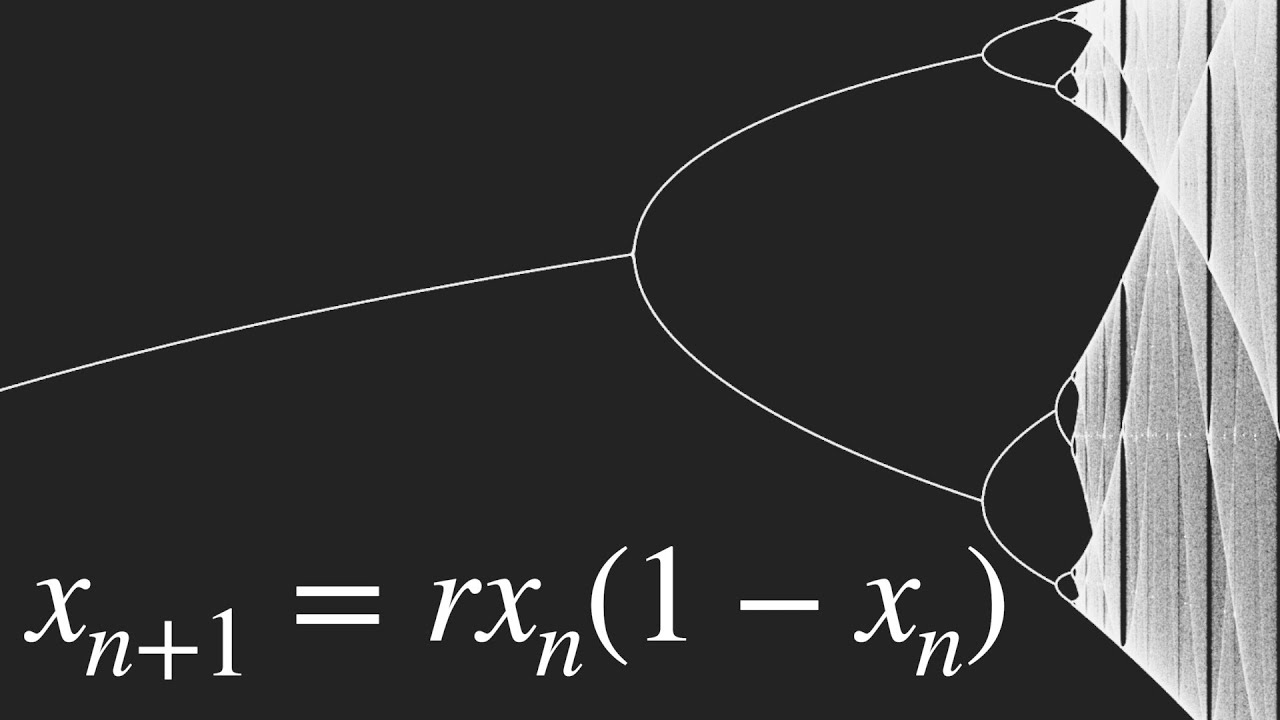
This equation will change how you see the world (the logistic map)

Introduction to Random Variables Probability Distribution

Greatest Math Theories Explained

Lucky Numbers Based on Age & Birth Year! Unlock Abundance & Fortune Now
5.0 / 5 (0 votes)
