Garis Singgung Persekutuan Dalam dan Luar #garissinggunglingkaran #matematika
Summary
TLDRThis tutorial video from Ompeng Tutorial explains how to calculate the length of common tangents between two circles, covering both internal and external tangents. Using clear explanations and step-by-step examples, it demonstrates how to apply the Pythagorean theorem to find tangent lengths based on circle radii and the distance between centers. The instructor provides example problems with detailed calculations, showing how to determine tangent lengths accurately. The video concludes by encouraging viewers to engage with the channel by liking, commenting, and subscribing for more educational content.
Takeaways
- 😀 Understanding the concept of common tangents between two circles, which can be classified into inner and outer tangents.
- 😀 The common tangent line connects two circles, with each circle having a radius that helps determine the tangent length.
- 😀 The formula for calculating the **inner common tangent** is based on the Pythagorean theorem: m² = D² - (r_A - r_B)².
- 😀 The formula for calculating the **outer common tangent** is also based on the Pythagorean theorem: m² = D² - (r_A + r_B)².
- 😀 The Pythagorean theorem is crucial for calculating the tangent lengths, where D is the distance between the centers of the circles and r_A and r_B are the radii of the respective circles.
- 😀 For an inner common tangent, you subtract the difference between the radii from the distance between the centers, while for an outer tangent, you add the radii.
- 😀 A practical example demonstrates how to apply the formula for inner tangents, with the final result being approximately 28.28 cm for a given pair of circles.
- 😀 In the case of the outer tangent, the calculation results in a length of approximately 9.80 cm, showing how the formula for outer tangents differs slightly.
- 😀 Clear steps for calculating the inner common tangent: square the distance between centers, subtract the square of the difference of radii, and then take the square root.
- 😀 Clear steps for calculating the outer common tangent: square the distance between centers, subtract the square of the sum of the radii, and then take the square root.
Q & A
What are the two types of common tangents for two circles discussed in the video?
-The two types of common tangents are the inner common tangent and the outer common tangent.
How is the length of the common tangent denoted in the video?
-The length of the common tangent is denoted as 'M', and is symbolized as 'PQ' or 'MP' in the context of the explanation.
What geometric principle is used to calculate the length of the common tangent?
-The Pythagorean theorem is used to calculate the length of the common tangent.
How is the length of the common tangent for the inner common tangent calculated?
-For the inner common tangent, the formula is M² = D² - (R₁ + R₂)², where D is the distance between the centers of the circles, and R₁ and R₂ are the radii of the two circles.
How is the length of the common tangent for the outer common tangent calculated?
-For the outer common tangent, the formula is M² = D² - (R₁ - R₂)², where D is the distance between the centers of the circles, and R₁ and R₂ are the radii of the two circles.
In the video example, what is the distance between the centers of the two circles used to calculate the common tangent?
-In the example, the distance between the centers of the two circles is 30 cm.
What are the radii of the two circles in the example used to calculate the common tangent?
-In the example, the radius of circle P is 14 cm, and the radius of circle Q is 4 cm.
What is the final result for the length of the common tangent in the first example?
-The final result for the length of the common tangent in the first example is 24 cm.
How does the video explain the method for finding the length of the outer common tangent in the second example?
-In the second example, the method involves using the formula M² = D² - (R₁ - R₂)², where the distance between the centers of the circles (D) is 25 cm, the radius of the larger circle (R₁) is 15 cm, and the radius of the smaller circle (R₂) is 8 cm.
What is the result for the length of the outer common tangent in the second example?
-The length of the outer common tangent in the second example is also 24 cm.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Garis Singgung Lingkaran(2) - Garis Singgung Persekutuan Luar dan Dalam | Matematika Kelas 8 SMP MTs
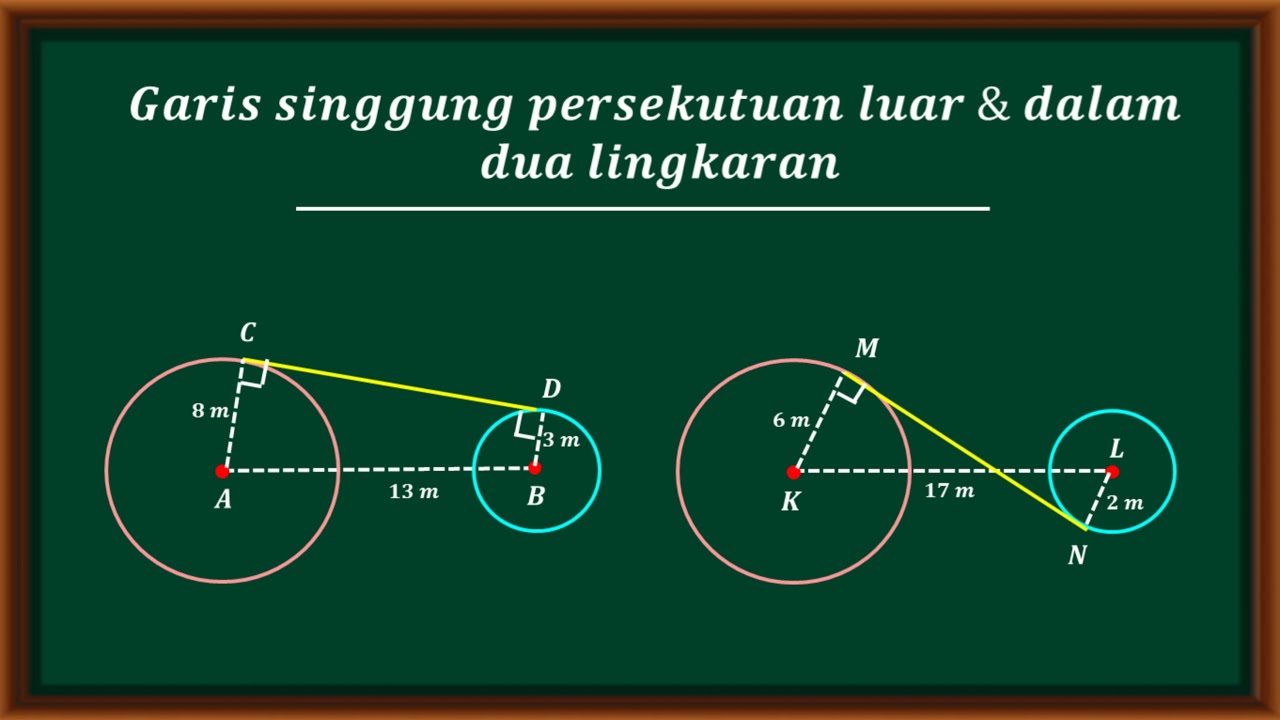
Garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran

Garis Singgung Lingkaran | Matematika SMA Kelas XI
Garis Singgung Lingkaran (2) - Garis Singgung Persekutuan Luar dan Dalam - Matematika SMP

Materi Matematika Kelas 8: Lingkaran

2nd Quarter Grade 10 Math -( Lesson 5) Illustrating Secant, Tangent, Sector and Segment of a Circle
5.0 / 5 (0 votes)
