Calculus - Introduction to Calculus
Summary
TLDRThis video script introduces the concept of Calculus as the study of change, contrasting it with more static mathematical fields. It uses relatable examples, such as a car's variable speed and a deflating balloon's volume, to illustrate the need for calculus to understand these dynamic situations. The script emphasizes three fundamental tools of calculus: limits, derivatives, and integrals, which are essential for describing functions' behavior over time. It highlights the interconnectedness of these concepts and the practical applications of calculus in various real-world scenarios, encouraging viewers to delve deeper into the subject.
Takeaways
- 🎓 Calculus is the branch of mathematics that deals with change and is essential for understanding dynamic phenomena.
- 🚗 The script introduces the concept of calculus with a driving car example, illustrating the need for a mathematical framework to handle changing speeds.
- 🌐 Another example given is a deflating balloon, emphasizing the relationship between changing volume and radius, and the need for calculus to describe such relationships.
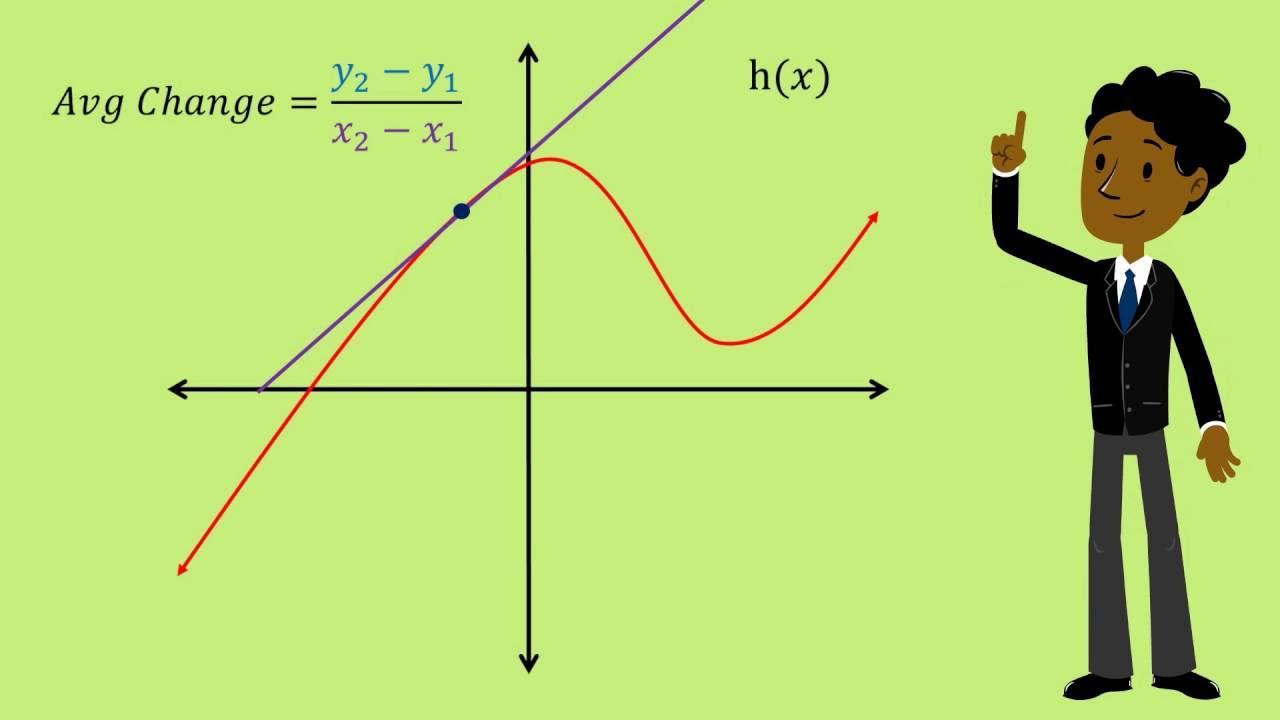
- 🛠️ Calculus employs three fundamental tools: limits, derivatives, and integrals, which are crucial for solving problems involving change.
- 📌 Limits describe how a function approaches a value, which is foundational for understanding the behavior of functions as they approach certain points.
- 📈 Derivatives are used to describe the rate of change of a function, providing insights into how fast something is changing at any given moment.
- 📊 Integrals calculate the accumulated change under a curve, often used to find areas, volumes, or total quantities over a period.
- 🔗 The script highlights the interconnectedness of derivatives and integrals, with derivatives being constructed from limits and integrals being their inverses.
- 🧠 Learning calculus is challenging due to its new concepts, terminology, and procedures, but it's essential for a deeper understanding of the world's dynamics.
- 🌟 Calculus has practical applications, such as optimizing viewing positions in a theater or designing the perfect soup can, showcasing its real-world relevance.
- 📚 The speaker invites viewers to explore more calculus content through their videos, suggesting a comprehensive learning resource for those interested.
- 📺 The video concludes with an invitation to like, subscribe, and visit the speaker's website for more calculus-related content and example problems.
Q & A
What is the main focus of calculus?
-The main focus of calculus is to deal with change, particularly in quantities that are continuously varying.
Why is calculus different from other areas of mathematics?
-Calculus is different because it specifically addresses the mathematics of change, unlike other areas of math that may deal with static or unchanging quantities.
What is an example given in the script to illustrate the concept of change in calculus?
-The example of a car with changing speed over a 3-hour period is given to illustrate the concept of change in calculus.
How does calculus help in determining the distance traveled by a car with changing speed?
-Calculus uses concepts such as derivatives to determine the distance traveled by a car with changing speed over a given time period.
What is another example provided in the script to demonstrate the application of calculus?
-The script provides the example of modeling the volume of a deflating balloon to demonstrate the application of calculus.
How is the volume of a balloon related to its radius?
-The volume of a balloon is related to its radius by the formula V = 4/3 * pi * r^3, where V is the volume and r is the radius.
What are the three main tools of calculus mentioned in the script?
-The three main tools of calculus mentioned are limits, derivatives, and integrals.
What is the purpose of limits in calculus?
-Limits are used in calculus to precisely describe how a function approaches a value.
What do derivatives in calculus represent?
-Derivatives in calculus represent the rate of change of a function, providing insight into how the function changes.
What is the significance of integrals in calculus?
-Integrals in calculus are used to calculate the area under the curve of a function, which can represent accumulated change over a period.
How are derivatives and integrals related in the context of calculus?
-Derivatives and integrals are related because integrals can be viewed as the inverse operation of derivatives; they are two sides of the same coin in describing change.
What is the script's final call to action for the viewer?
-The script encourages the viewer to watch more calculus videos, subscribe to the channel, and visit the website MySecretMathTutor.com for more information.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)