Gaussian Elimination In Python | Numerical Methods
Summary
TLDRIn this video, the process of implementing Gaussian elimination in Python is explored step-by-step. The method starts with a quick review of the theory, transforming a square system of linear equations into an upper triangular matrix. The Python implementation involves using the NumPy library to handle matrices, checking for correct input dimensions, and constructing an augmented matrix. The Gauss elimination process is carried out row by row, followed by backward substitution to solve for unknown variables. The video also covers potential errors and debugging, making it an essential guide for coding Gauss elimination in Python.
Takeaways
- 😀 Gaussian elimination is a method to solve square linear systems by transforming the system into an upper triangular matrix.
- 😀 The process involves creating an augmented matrix and systematically eliminating elements below the main diagonal.
- 😀 Backward substitution is used to solve for unknown variables starting from the last row of the upper triangular matrix.
- 😀 In Python, the NumPy library is recommended for handling matrices efficiently.
- 😀 When implementing Gaussian elimination in Python, it is important to check that the coefficient matrix is square and that the constant vector has compatible dimensions.
- 😀 Initializing variables such as the solution vector and iteration counters is crucial before starting the elimination process.
- 😀 Forward elimination is performed row by row, using scaling factors to zero out elements below the diagonal.
- 😀 Diagonal elements should not be zero; otherwise, the algorithm may fail, and partial pivoting is recommended for handling such cases.
- 😀 Backward substitution involves computing each unknown variable using the already solved values from lower rows.
- 😀 Displaying results clearly helps users understand and verify the solution of the system.
- 😀 Testing the function with example matrices ensures the correctness of the Gaussian elimination implementation.
- 😀 Visualizing intermediate matrices, like the augmented matrix and upper triangular form, can help identify errors and improve understanding of the algorithm.
Q & A
What is Gaussian elimination and why is it used?
-Gaussian elimination is a method used to solve systems of linear equations. It transforms the system's matrix into an upper triangular matrix, which makes it easier to solve the system using backward substitution.
What does the process of Gaussian elimination involve?
-The process involves two main steps: (1) transforming the matrix into an upper triangular matrix by reducing elements below the main diagonal to zero, and (2) using backward substitution to solve for the unknown variables, starting from the bottom row and working upwards.
Why is it important to use the numpy library for matrix operations in Python?
-The numpy library is crucial because it simplifies working with matrices and allows efficient manipulation and calculation of matrix operations like concatenation and element-wise operations, which are essential for implementing Gaussian elimination.
How do you import numpy in Python and what IDE is used in the tutorial?
-In the tutorial, numpy is imported by installing it through the interpreter settings in PyCharm, an integrated development environment (IDE). The library is installed by searching for it in the package manager and clicking 'Install Package'.
What contingency checks are added to ensure proper matrix input in the Gaussian elimination function?
-The function checks that the A matrix is square (i.e., the number of rows equals the number of columns), and that the B matrix is a column vector with a number of rows matching the A matrix. If these conditions are not met, the function returns an error.
Why is it necessary to convert the augmented matrix to a float data type?
-Converting the augmented matrix to a float ensures that the calculations are accurate and prevents truncation errors that may arise if integers are used, as they could lead to imprecise results due to rounding.
What happens if there is a zero in the main diagonal of the matrix?
-If there is a zero on the main diagonal, the scaling factor formula used in Gaussian elimination would cause issues. In such a case, an error message is displayed, and the function terminates to prevent incorrect calculations.
How is backward substitution performed in the Gaussian elimination process?
-Backward substitution starts from the last row of the augmented matrix. The solution for the unknown variable corresponding to the last row is found first, then the remaining variables are solved row by row, moving upward, using previously calculated values.
What is the role of the 'range' function in the backward substitution step?
-The 'range' function is used to iterate through the rows of the matrix starting from the second last row and moving upwards. It helps in applying the necessary operations on each row to solve for the unknown variables sequentially.
Why is it useful to visualize the code using print statements?
-Visualizing the code with print statements helps track the progress of the Gaussian elimination algorithm. It allows users to identify any errors early, understand how the matrix is being transformed at each step, and confirm that the algorithm is working as expected.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
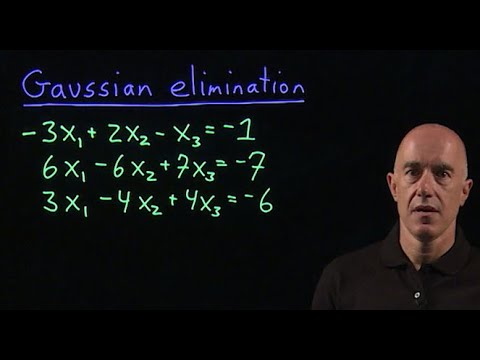
Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers
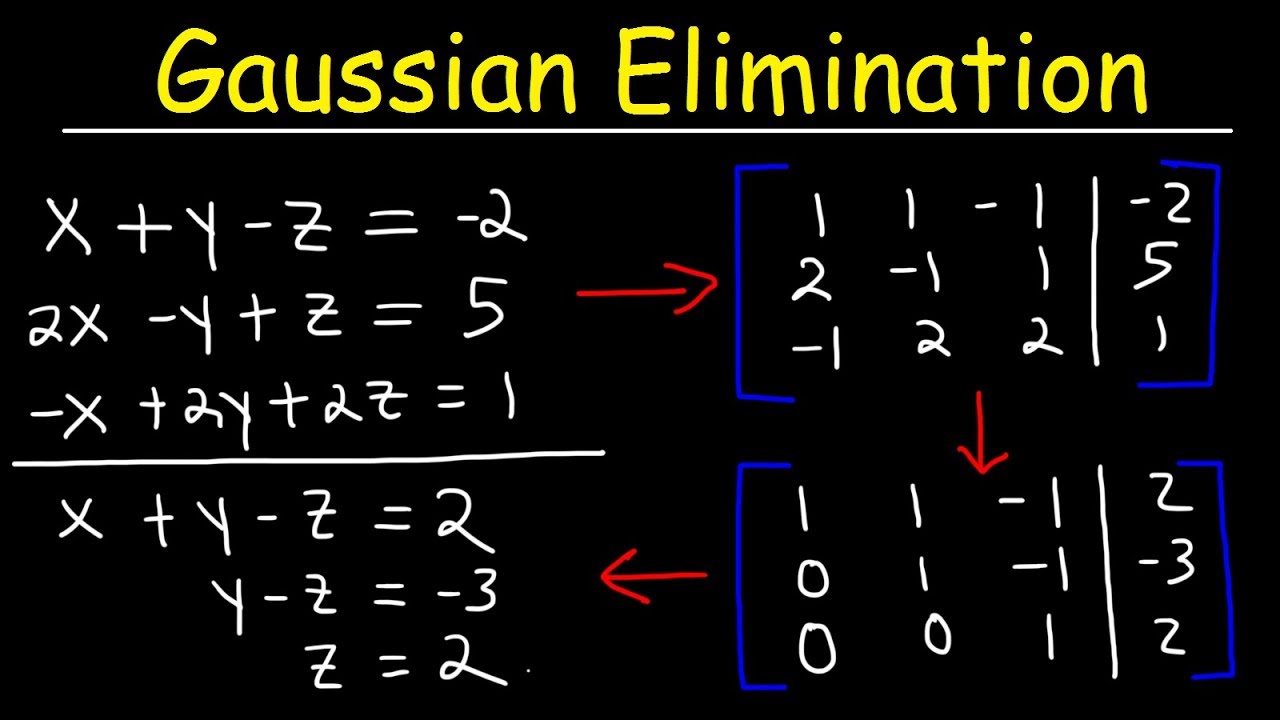
Gaussian Elimination & Row Echelon Form

SERI KULIAH ALJABAR LINEAR ELEMENTER || KOMBINASI LINEAR
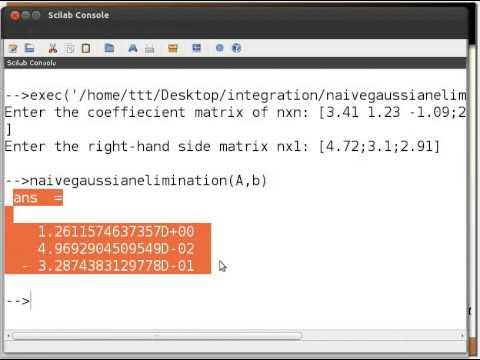
Linear equations Gaussian Methods - English

Gauss-Jordan Elimination

#19 Teori Bahasa & Otomata - Contoh penyederhanaan aturan produksi Context Free Grammar
5.0 / 5 (0 votes)
