Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers
Summary
TLDRIn this video, the Gaussian elimination algorithm for solving systems of linear equations is explained step by step. The process begins with matrix representation, where a system of equations is transformed into an augmented matrix. The video demonstrates key operations, such as row swaps and scaling, to bring the matrix to an upper triangular form. Once this is achieved, back substitution is used to efficiently solve for the unknowns. Gaussian elimination is essential in large-scale computations, allowing for fast solutions to complex systems, making it an indispensable tool in both mathematics and computer science.
Takeaways
- 😀 Gaussian elimination is a key algorithm used to solve systems of linear equations, essential for large-scale computations.
- 😀 Matrices are used to represent systems of linear equations in a compact and efficient manner.
- 😀 The augmented matrix is formed by appending the right-hand side values to the matrix of coefficients.
- 😀 Allowed operations on the system include reordering equations, multiplying an equation by a constant, and adding one equation to another.
- 😀 The goal of Gaussian elimination is to transform the matrix into an upper triangular form to simplify solving.
- 😀 The pivot element in each row is used to eliminate all elements below it by manipulating the other rows.
- 😀 Once the matrix is in upper triangular form, solving becomes easy through back substitution, starting from the last equation.
- 😀 Back substitution allows for efficient computation by solving for variables from the bottom row upwards.
- 😀 The efficiency of Gaussian elimination makes it suitable for solving systems with large numbers of equations and unknowns.
- 😀 For a system of equations represented as Ax = b, the solution can be computed using Gaussian elimination faster than using matrix inversion.
Q & A
What is the main algorithm discussed in the video?
-The main algorithm discussed in the video is Gaussian elimination, which is used for solving systems of linear equations.
Why is Gaussian elimination important for computers?
-Gaussian elimination is important because computers often solve large systems of linear equations with thousands of equations and unknowns, and Gaussian elimination provides an efficient method for doing so.
What is the purpose of matrices in solving linear systems?
-Matrices are used to represent linear systems of equations, allowing the system to be expressed as a matrix equation Ax = b, where A is the coefficient matrix, x is the vector of unknowns, and b is the right-hand side vector.
What is an augmented matrix?
-An augmented matrix is formed by attaching the right-hand side vector (b) as the last column to the matrix A, creating a combined matrix that represents the system of equations.
What operations can be performed on the augmented matrix without changing the solution?
-The allowed operations are: changing the order of the equations (or rows of the matrix), multiplying any row by a constant, and adding a multiple of one row to another row.
What is the goal of Gaussian elimination?
-The goal of Gaussian elimination is to transform the matrix into an upper triangular form, which makes it easier to solve the system using back substitution.
What is the pivot position in Gaussian elimination?
-The pivot position is the first non-zero element in a row, and it is used to eliminate the numbers below it by performing row operations.
How does back substitution work in solving a system after Gaussian elimination?
-Back substitution starts with the last equation, solving for the unknowns in reverse order. As each value is found, it is substituted into the equations above it, progressively solving for all unknowns.
Why is Gaussian elimination considered efficient for large-scale systems?
-Gaussian elimination is efficient because it reduces the computational complexity of solving large systems of linear equations, allowing computers to solve them with fewer operations.
What is the final solution obtained from the system of equations in the video?
-The final solution to the system of equations in the video is x1 = 2, x2 = 2, and x3 = -1.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
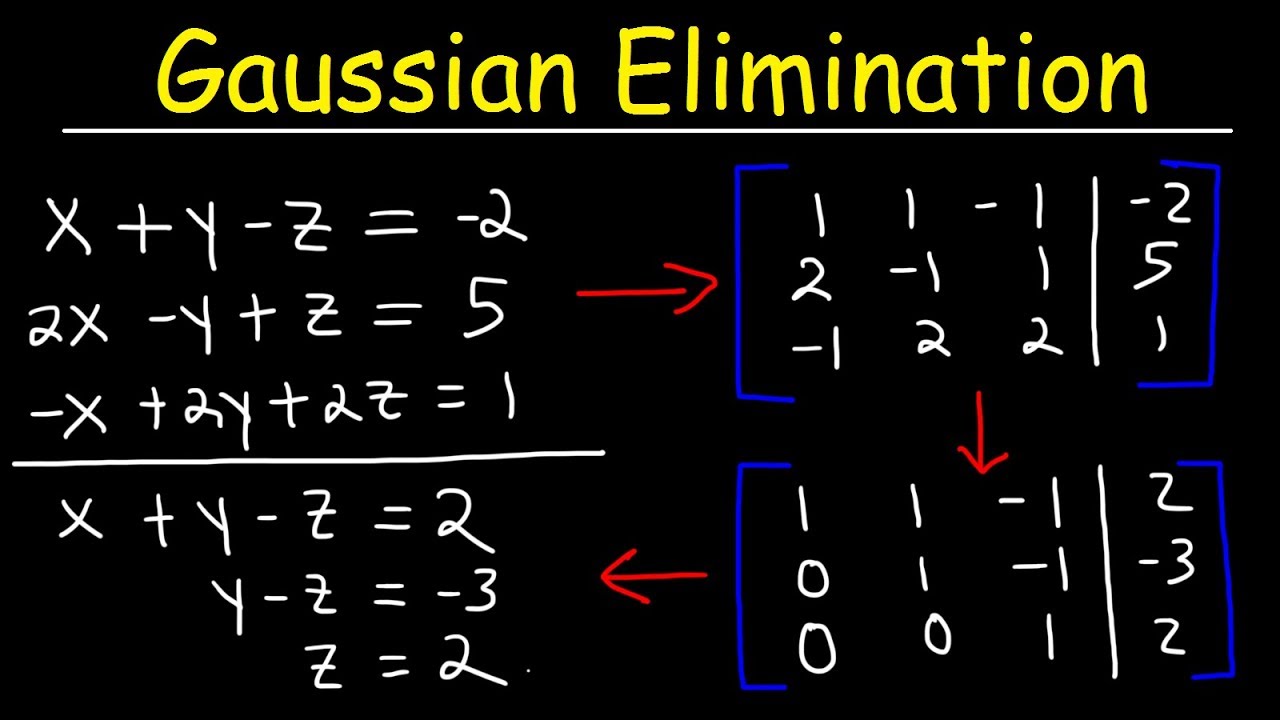
Gaussian Elimination & Row Echelon Form
Linear equations Gaussian Methods - English

SERI KULIAH ALJABAR LINEAR ELEMENTER || KOMBINASI LINEAR

SPLDV (Substitusi, Eliminasi, Campuran)

SPLTV #Part 4 // Metode Gabungan // Sistem Persamaan Linear Tiga Variabel

Solving Systems of Equations By Elimination & Substitution With 2 Variables
5.0 / 5 (0 votes)