Cálculo de área entre una parábola y 2 rectas con INTEGRALES DOBLES | GEOGEBRA y MAPLE
Summary
TLDREn este video, se resuelve un interesante problema de cálculo de áreas utilizando integrales dobles. El ejercicio se centra en encontrar el área entre una parábola y una recta sobre el eje X. A lo largo del video, se explica cómo identificar puntos clave como el vértice de la parábola y los puntos de intersección con la recta y el eje X. El enfoque principal es dividir la región en dos áreas y usar integrales dobles para calcular el área total. Además, se presenta una verificación del resultado mediante el software Maple y se destaca la importancia de comprender la técnica de integración con diferencias verticales.
Takeaways
- 😀 El ejercicio trata sobre el cálculo del área entre una parábola, una recta y el eje x utilizando integrales dobles.
- 😀 El problema se enfoca en cómo resolver un área delimitada por una parábola y una recta, y se explica que también se podría hacer con integrales simples.
- 😀 Se analiza la parábola y = 2 - x², la cual abre hacia abajo, y se determinan los puntos de corte con el eje x.
- 😀 Se demuestra cómo calcular los puntos de intersección entre la parábola y la recta y = x utilizando igualación y factorización.
- 😀 Se identifican dos áreas principales en el gráfico: una entre la parábola y el eje x, y otra entre la parábola y la recta y = x.
- 😀 Para resolver el área, se debe dividir el problema en dos áreas separadas, ya que la parábola corta al eje x, creando dos regiones distintas.
- 😀 Se utiliza una orientación vertical para las integrales dobles, lo que facilita el cálculo al integrar de abajo hacia arriba.
- 😀 La solución final para el área total implica sumar las dos áreas separadas, cada una con sus propios límites de integración.
- 😀 El cálculo del área se realiza utilizando integrales dobles con funciones polinómicas, y se evalúan en los puntos de corte obtenidos previamente.
- 😀 Se verifica el resultado utilizando el programa Maple, lo que demuestra la validez de la solución obtenida manualmente.
- 😀 El ejercicio es una excelente práctica para comprender el uso de integrales dobles en cálculo multivariable y cómo dividir áreas complicadas en partes más simples.
Q & A
¿Qué tipo de problema se está resolviendo en el video?
-El problema trata sobre el cálculo del área entre una parábola, una recta y el eje X, utilizando integrales dobles.
¿Cuál es la ecuación de la parábola mencionada en el video?
-La parábola tiene la ecuación y = 2 - x^2, que es una parábola que abre hacia abajo.
¿Qué puntos de interés se identifican en la parábola?
-Se identifican tres puntos importantes: el vértice en (0, 2) y dos puntos de corte con el eje X en x = -√2 y x = √2.
¿Cómo se determinan los puntos de corte con el eje X?
-Los puntos de corte se obtienen resolviendo la ecuación y = 0, es decir, 2 - x^2 = 0, lo que da como soluciones x = -√2 y x = √2.
¿Qué ocurre cuando se introduce la recta y = x en el problema?
-La recta y = x se introduce para ver cómo se interseca con la parábola, lo que complica el problema al añadir otra región sobre el eje X.
¿Cómo se determinan los puntos de intersección entre la parábola y la recta y = x?
-Se igualan las ecuaciones de la parábola y la recta, 2 - x^2 = x, y se resuelve la ecuación cuadrática obteniendo los puntos de corte en x = -1 y x = 1.
¿Cuáles son las dos áreas que se deben calcular en el problema?
-Las dos áreas son: una entre la parábola y el eje X desde x = -√2 a x = 0, y otra entre la parábola y la recta y = x desde x = 0 a x = 1.
¿Por qué se utiliza la orientación vertical en la integración doble?
-Se utiliza la orientación vertical porque la ecuación de la parábola está despejada para y, lo que facilita la integración en términos de x y y.
¿Qué fórmula se utiliza para calcular el área total en este problema?
-El área total se obtiene sumando las dos integrales dobles, una para el área entre la parábola y el eje X, y otra entre la parábola y la recta y = x.
¿Cómo se verifica el resultado del cálculo del área?
-El resultado del área se verifica utilizando el programa Maple, que calcula la integral doble y produce el mismo resultado que el cálculo manual.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Volumen de z= xy con integral doble | COORDENADAS POLARES | Ej. 33 Sección 14.3 LARSON | GEOGEBRA

Volumen entre 2 cilindros verticales y logaritmo natural | POLARES | Ej. 36 Sección 14.3 LARSON
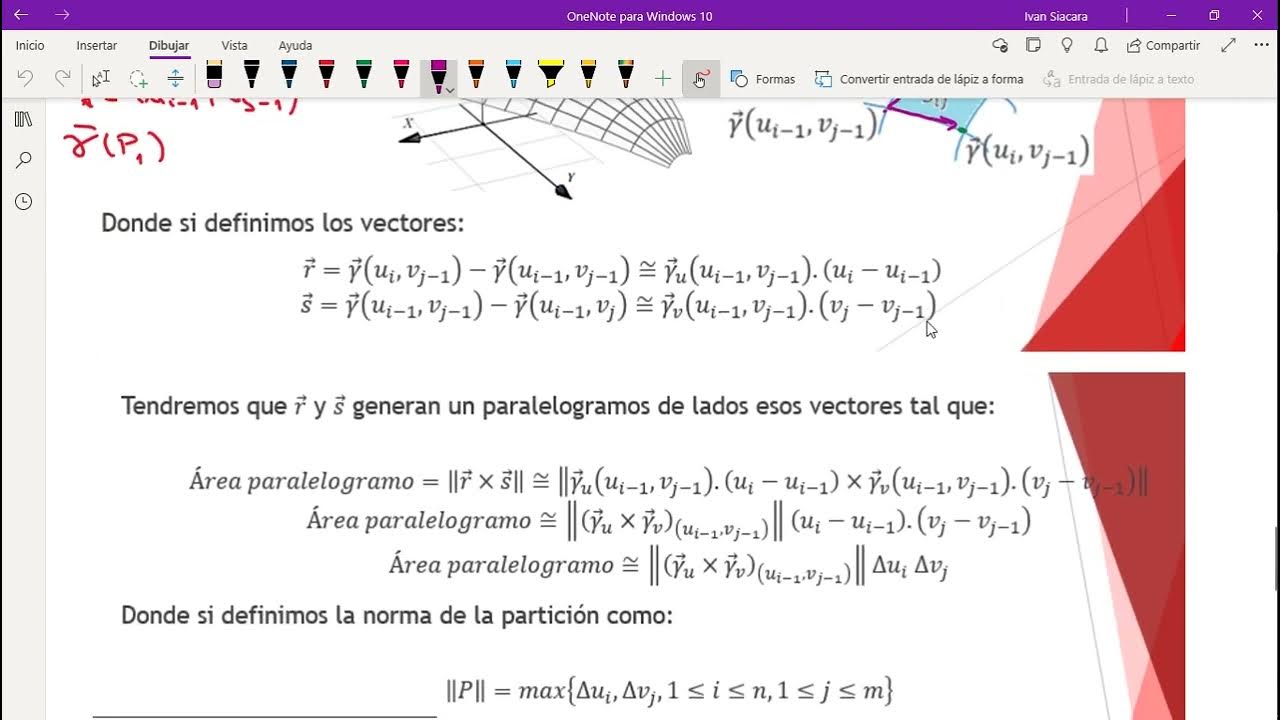
Clase 16 (2da Parte): Integrales de Superficie (campos escalares)

Volumen entre paraboloide y cilindro con integral doble | POLARES | Ej. 34 Sección 14.3 LARSON

Integral doble sobre regiones generales

4 Teorema de Green
5.0 / 5 (0 votes)
