Pembahasan Latihan Soal Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka
Summary
TLDRIn this educational video, the presenter explains how to solve a circle arc length problem. The scenario involves a circle with points A and B, a given central angle of 120 degrees, and a radius of 18 cm. The video walks viewers through the process of calculating the length of the minor arc AB using a formula. After analyzing the given data, the presenter demonstrates how to substitute values into the formula and simplify to get the final result: 12π cm. The video aims to help viewers understand and solve similar problems with clarity and confidence.
Takeaways
- 😀 The video explains how to calculate the length of an arc in a circle using a given central angle and radius.
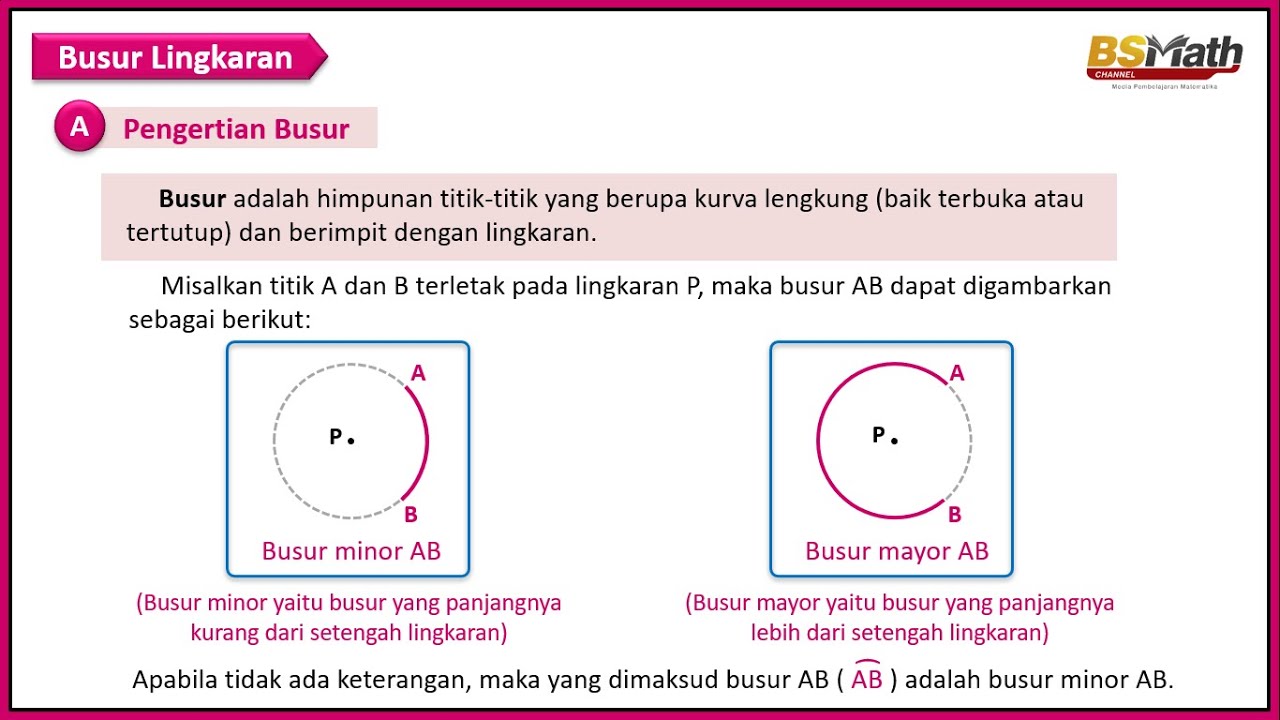
- 😀 The problem involves a circle with points A and B on the circumference, and the central angle between them is 120°.
- 😀 The radius of the circle is given as 18 cm, and the objective is to find the length of the minor arc AB.
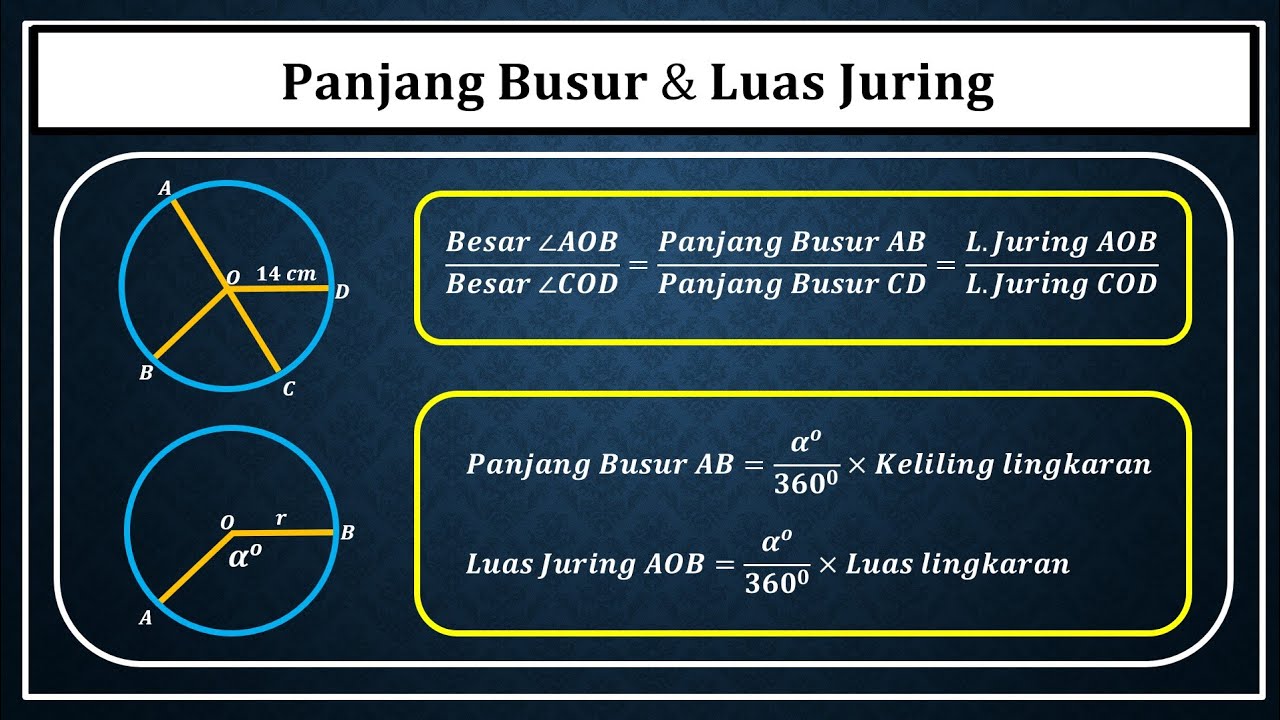
- 😀 The formula to calculate the length of an arc is: Arc Length = (A / 360°) × 2πr.
- 😀 The central angle A is 120°, and the radius r is 18 cm, which are substituted into the arc length formula.
- 😀 The angle 120° is simplified as 120/360 = 1/3, which is then used in the formula to calculate the arc length.
- 😀 The formula becomes (1/3) × 2 × 18 × π, simplifying to 12π cm as the length of the arc.
- 😀 The correct answer is 12π cm, which corresponds to option C in the provided multiple-choice answers.
- 😀 The presenter emphasizes the importance of simplifying fractions and keeping π as is (not replacing with 3.14 or 22/7).
- 😀 The video concludes by thanking the viewers for participating and encouraging them to keep practicing and stay motivated in their studies.
Q & A
What is the main topic of the video?
-The video explains how to solve a problem related to finding the length of an arc in a circle.
What are the given values in the problem?
-The given values in the problem are a central angle of 120° and a radius of 18 cm.
What formula is used to find the length of an arc?
-The formula used is: Arc length = (θ / 360°) * 2πr, where θ is the central angle and r is the radius.
How is the central angle used in the formula?
-The central angle (θ) is used to find the fraction of the circle that the arc represents by dividing it by 360°, the total degrees in a circle.
What is the value of the central angle in the given problem?
-The value of the central angle is 120°.
How is the radius represented in the formula?
-The radius is represented as 'r' in the formula, and in this problem, it is given as 18 cm.
Why is π (pi) not substituted with a numerical value in the answer?
-Pi (π) is not substituted with a numerical value because the options in the answer choices include π, so it is kept as π for consistency.
What does the simplification of 120/360 result in?
-The simplification of 120/360 results in 1/3.
What is the final length of the arc AB?
-The final length of the arc AB is 12π cm.
How does the simplification of the expression help in solving the problem?
-Simplifying the fraction 120/360 to 1/3 makes the calculation easier, as it reduces the complexity of the expression and allows for quick multiplication to find the arc length.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)