Tensors for Beginners 0: Tensor Definition

Summary

In this video, the presenter introduces the concept of tensors by offering multiple definitions. Initially, tensors are defined as multi-dimensional arrays, but this is revised to emphasize their geometrical nature and coordinate invariance. The explanation touches on components of tensors transforming predictably under changes in coordinate systems and introduces the idea of tensors as collections of vectors and covectors. The video also hints at more advanced uses of tensors in calculus, especially in general relativity, while preparing the viewer for future mathematical applications in upcoming videos.

Takeaways

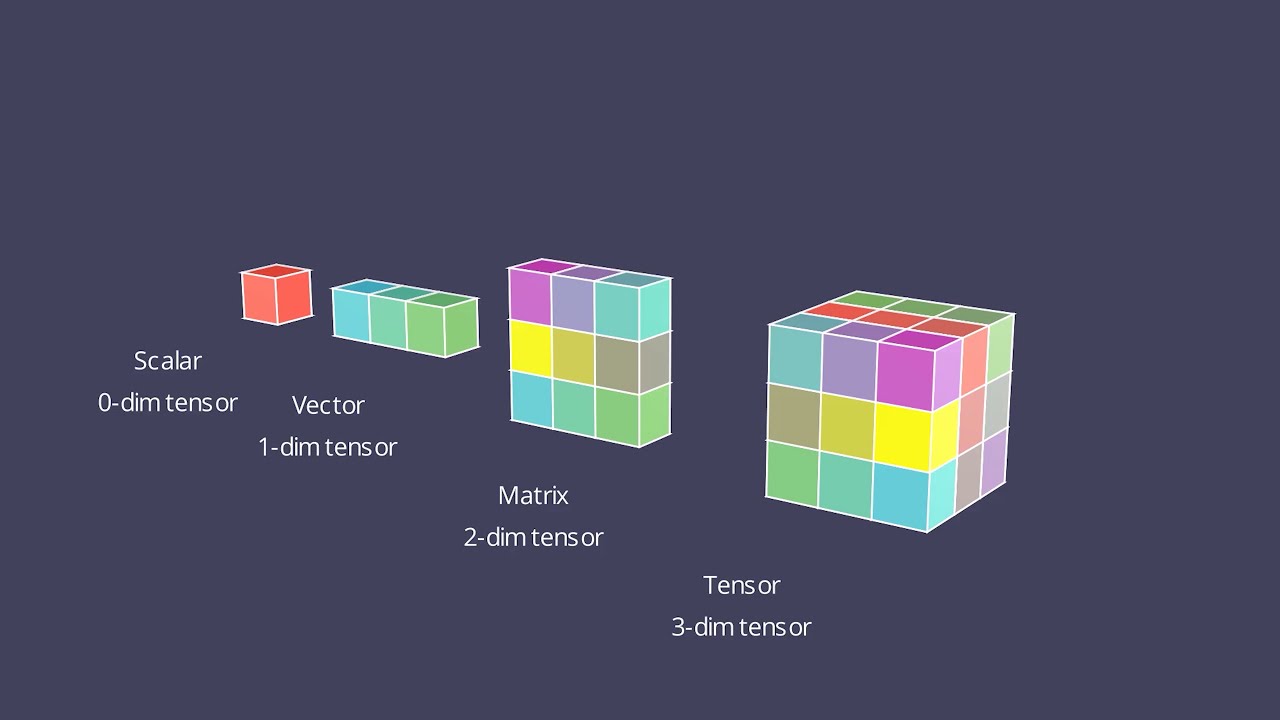
• 😀 A tensor is a multi-dimensional array of numbers, often referred to as a grid of numbers.
• 😀 Scalars are rank zero tensors, essentially single numbers like 1, 2, pi, etc.
• 😀 Vectors are rank one tensors, representing one-dimensional arrays or lists of numbers.
• 😀 Matrices are rank two tensors, which are two-dimensional arrays with rows and columns.
• 😀 Tensors can have higher ranks, like rank 3, 4, and so on, representing multi-dimensional arrays.
• 😀 The array definition of a tensor is a simple way to think of tensors, but it misses the deeper geometric meaning behind them.
• 😀 A more accurate definition of a tensor is that it is invariant under a change of coordinates, but its components change in a predictable way.
• 😀 The components of a tensor depend on the chosen coordinate system, but the tensor itself remains invariant.
• 😀 The transformation of a tensor's components when switching between coordinate systems is called forward and backward transformations.
• 😀 The most abstract and complete definition of a tensor is that it is a combination of vectors and covectors using the tensor product.
• 😀 Tensors appear in calculus as partial derivatives and gradients, and transform with the Jacobian matrix in curved geometries like those seen in general relativity.

Q & A

What is the basic idea behind tensors?

Tensors are multi-dimensional arrays of numbers, but their true significance lies in their geometrical meaning, which involves invariance under a change of coordinates and predictable transformations of components across different coordinate systems.

What is a scalar, and how is it related to tensors?

A scalar is a rank-zero tensor, which is simply a single number like 1, 2, or pi. Though typically not written as an array, it can be represented in an array form to illustrate its relationship with tensors.

How does a vector relate to tensors?

A vector is a rank-one tensor, which is essentially a one-dimensional array of numbers that can be thought of as extending in a single direction.

What is the significance of a matrix in the context of tensors?

A matrix is a rank-two tensor, a two-dimensional grid of numbers. It represents the concept of extending numbers in two dimensions, horizontally and vertically. It is also used to describe entities like the metric tensor in general relativity.

What is meant by the 'array definition' of a tensor?

The 'array definition' of a tensor refers to the idea of a tensor being a multi-dimensional array (like a scalar, vector, or matrix), but this definition is incomplete because it overlooks the deeper geometrical significance of tensors.

Why is the array definition of a tensor considered incorrect?

The array definition is incorrect because it only focuses on the numerical arrangement of tensor components and ignores the fundamental geometrical properties of tensors, which are crucial for understanding their true nature.

What does it mean for a tensor to be 'invariant' under a change of coordinates?

A tensor is invariant under a change of coordinates if its intrinsic properties, like length or orientation, do not change, regardless of the coordinate system used. This means the tensor's essence remains constant across different perspectives.

What happens to the components of a tensor when the coordinate system changes?

The components of a tensor are not invariant; they change predictably when the coordinate system changes. The way they transform is governed by specific rules that can be understood through 'forward' and 'backward' transformations.

What is the relationship between coordinate systems and tensor components?

Different coordinate systems provide different sets of components for the same tensor. These components change depending on the choice of coordinate system, but the tensor itself remains invariant under such transformations.

What is the 'abstract definition' of a tensor?

The 'abstract definition' of a tensor describes it as a collection of vectors and covectors combined using the 'tensor product'. This definition is more precise but requires understanding vectors, covectors, and the tensor product before it can be fully appreciated.