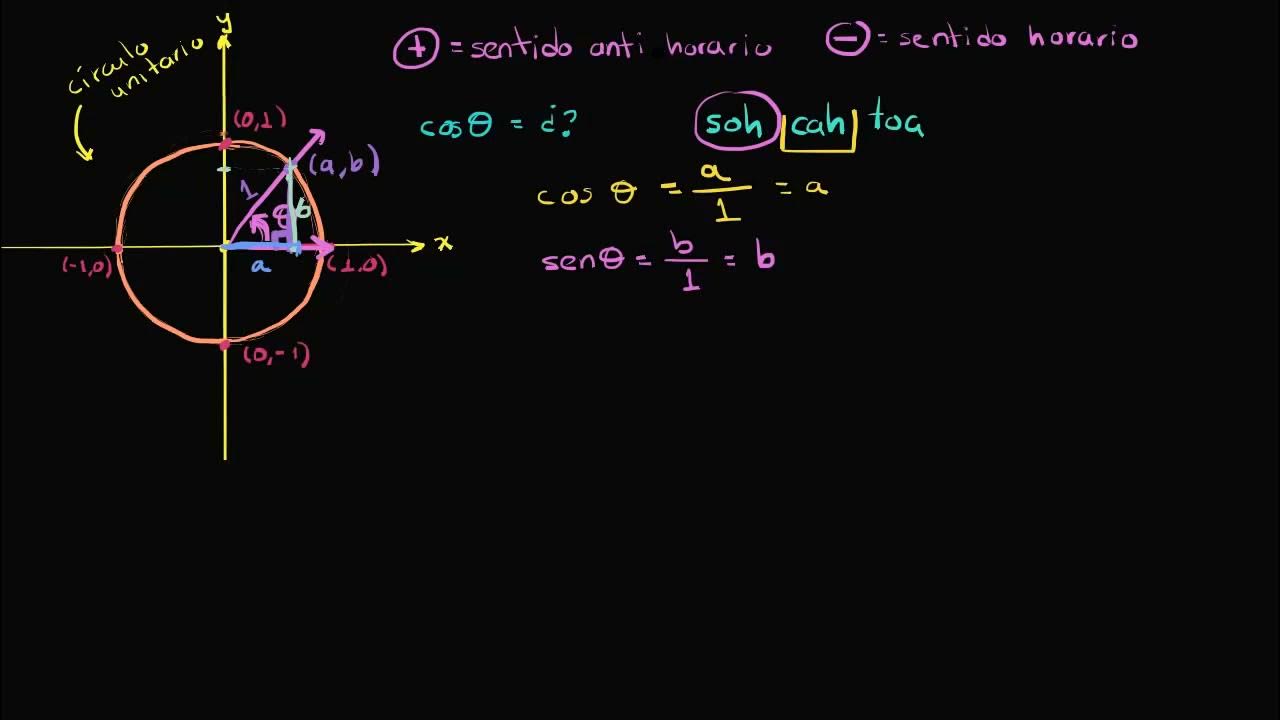Circunferência trigonométrica -- Geogebra

Summary

In this video, Professor Kit Guedes introduces the concept of reducing angles in the unit circle using GeoGebra software. The focus is on understanding how to reduce angles greater than 360° to the first rotation (0° to 360°). Through various examples, such as reducing 375°, 405°, 750°, 930°, and 5000° angles, viewers learn how to subtract full rotations (360°) to find the equivalent angle within the first rotation. The lesson emphasizes the idea of congruent angles, which share the same terminal point on the unit circle, and teaches how to compute these reductions step by step.

Takeaways

• 😀 The video introduces GeoGebra, a free software tool that is used to demonstrate concepts in trigonometry, specifically focusing on the unit circle.
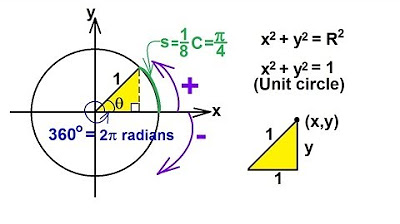
• 😀 The unit circle has a radius of 1, and the origin of the circle is the center for the angle measurements.
• 😀 The goal is to reduce angles greater than 360° to their corresponding angles within the first rotation (i.e., the first 360°).
• 😀 If an angle exceeds 360°, it is reduced by subtracting multiples of 360° to find its equivalent within one full rotation.
• 😀 Example: 375° is reduced by subtracting 360°, resulting in a reduced angle of 15°.
• 😀 The software allows users to interact with the unit circle and visualize angles by adjusting a slider, which shows the angle's movement around the circle.
• 😀 Angles like 405° are congruent to 45° because they have the same terminal side, even though they represent different rotations.
• 😀 Congruent angles refer to angles that share the same endpoint on the unit circle, regardless of how many rotations have been completed.
• 😀 For larger angles, such as 750°, the angle is divided by 360° to determine how many full rotations occur. In this case, two full rotations (720°) plus 30° remains.
• 😀 Larger angles, like 930°, are reduced similarly: 930° divided by 360° gives two full rotations (720°) and leaves 210°.
• 😀 The video explains that even angles as large as 5000° can be reduced to their equivalent within the first rotation by using the same method of subtraction and division by 360°.

Q & A

What is the unit circle in trigonometry?

The unit circle is a circle with a radius of 1, centered at the origin. It is used in trigonometry to represent angles, where a full turn around the circle equals 360°.

What happens when an angle is greater than 360° in the context of the unit circle?

When an angle is greater than 360°, it corresponds to multiple turns around the unit circle. To find the equivalent angle within the first turn, we subtract multiples of 360° until the angle falls between 0° and 360°.

How can we reduce an angle of 375° to its equivalent in the first turn?

To reduce 375°, subtract 360° from it, resulting in 15°. Therefore, 375° is congruent to 15°.

What does the term 'congruent angles' mean in the context of the unit circle?

Congruent angles are angles that have the same terminal side on the unit circle, even if the angles are different in magnitude. For example, 375° and 15° are congruent because they share the same terminal side.

What is the purpose of the 'slider control' in GeoGebra during this tutorial?

The slider control in GeoGebra is used to visually demonstrate how angles move along the unit circle. By adjusting the slider, users can see the corresponding angle and its position on the circle.

How can we reduce an angle of 405° to the first turn of the unit circle?

To reduce 405°, subtract 360° from it, resulting in 45°. Therefore, 405° is congruent to 45°.

What is the result when reducing an angle of 750° to the first turn of the unit circle?

To reduce 750°, divide 750° by 360°, which gives 2 full turns (720°) and leaves 30°. Therefore, 750° is congruent to 30°.

How do you reduce an angle of 930° to an equivalent angle within the first turn?

To reduce 930°, divide 930° by 360°, which gives 2 full turns (720°) and leaves 210°. Therefore, 930° is congruent to 210°.

What does it mean to 'reduce an angle to the first turn'?

Reducing an angle to the first turn means finding an equivalent angle that lies between 0° and 360°, by subtracting multiples of 360° until the angle falls within this range.

How would you reduce an angle of 5000° to the first turn?

To reduce 5000°, divide 5000° by 360°, which gives 13 full turns (4680°) and leaves 320°. Therefore, 5000° is congruent to 320°.