TRIGONOMETRÍA: Cos (a+b) Demostración de la fórmula Academia DIEGO
Summary
Please replace the link and try again.
Takeaways
- 😀 Der YouTube-Kanal vermittelt mathematische Konzepte auf einfache Weise, insbesondere in der Trigonometrie.
- 😀 In diesem Video geht es um den Beweis der Kosinusformel für die Summe von zwei Winkeln.
- 😀 Der Kanal bietet auch bereits Erklärungen zu anderen trigonometrischen Formeln, wie der Sinusformel für die Summe von zwei Winkeln.
- 😀 Ein wichtiger Punkt ist, dass der Kanal die Demonstration anhand von angrenzenden rechtwinkligen Dreiecken zeigt.
- 😀 Das Video erklärt die Bedeutung des Kosinus eines Winkels in Bezug auf benachbarte Seiten eines Dreiecks.
- 😀 Der Kosinus eines Winkels wird als Verhältnis von benachbartem Katheten zur Hypotenuse definiert.
- 😀 Die Kosinusformel der Summe von zwei Winkeln wird durch die Substitution bestimmter Längensegmente abgeleitet.
- 😀 Der Kosinus der Summe von zwei Winkeln ist durch die Formel: cos(A + B) = cos(A) * cos(B) - sin(A) * sin(B) definiert.
- 😀 Die Video-Demonstration nutzt die Ähnlichkeit von Dreiecken, um die Beziehung zwischen verschiedenen Segmenten zu verdeutlichen.
- 😀 Am Ende des Videos wird auf die Möglichkeit hingewiesen, den Kanal zu abonnieren und auf die Online- und Präsenzkurse der Akademie hinzuweisen.
Q & A
Was ist das Hauptthema des Videos?
-Das Hauptthema des Videos ist die Demonstration der Kosinusadditionformel in der Trigonometrie, speziell für cos(α + β).
Welche Figuren werden in der Beweisführung verwendet?
-In der Beweisführung werden zwei benachbarte rechtwinklige Dreiecke verwendet, die eine gemeinsame Seite teilen und deren Winkel α und β beinhalten.
Warum sind die beiden Dreiecke im Video ähnlich?
-Die beiden Dreiecke sind ähnlich, weil sie einen Winkel gemeinsam haben und zwei Seiten parallel sind. Diese Ähnlichkeit ermöglicht es, trigonometrische Beziehungen zwischen den Dreiecken abzuleiten.
Wie wird der Kosinus von α im Video definiert?
-Der Kosinus von α wird als das Verhältnis der benachbarten Kathete (gegenüber dem Winkel α) zur Hypotenuse des Dreiecks definiert.
Wie wird der Sinus von α im Video definiert?
-Der Sinus von α wird als das Verhältnis der gegenüberliegenden Kathete (gegenüber dem Winkel α) zur Hypotenuse des Dreiecks definiert.
Was passiert mit dem Segment AB, das für die Kosinusaddition benötigt wird?
-Das Segment AB, das die Kosinusaddition beschreibt, wird als Differenz von zwei Segmenten dargestellt: einem längeren Segment und einem kürzeren, der durch die Verwendung von trigonometrischen Funktionen berechnet wird.
Warum wird das Segment BC durch den Sinus von α ausgedrückt?
-Das Segment BC wird durch den Sinus von α ausgedrückt, weil es das gleiche Maß wie das Segment EF hat, das im ähnlichen Dreieck verwendet wird, und aufgrund der Definition des Sinus als Verhältnis von Kathete zu Hypotenuse.
Warum wird die Kosinusaddition als cos(α + β) = cos(α) * cos(β) - sin(α) * sin(β) formuliert?
-Die Kosinusaddition wird in dieser Formulierung dargestellt, weil durch das Ersetzen der Segmente mit den trigonometrischen Ausdrücken und die Verwendung von trigonometrischen Identitäten diese Beziehung zur Berechnung von cos(α + β) hergeleitet wird.
Welche weiteren trigonometrischen Formeln werden in zukünftigen Videos behandelt?
-In zukünftigen Videos werden auch die Formeln für den Sinus der Summe (sin(α + β)) sowie die Tangentenaddition und andere trigonometrische Identitäten behandelt.
Welche Rolle spielt die Ähnlichkeit der Dreiecke im Beweis?
-Die Ähnlichkeit der Dreiecke ist entscheidend, um trigonometrische Beziehungen zwischen den Seiten und Winkeln abzuleiten. Diese Beziehungen ermöglichen es, die Kosinusaddition auf der Grundlage von Sinus- und Kosinuswerten der einzelnen Winkel zu formulieren.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Binomios con término común. Demostración de la fórmula | Video 1 de 2.

Demostración de la fórmula de Herón. Parte 2
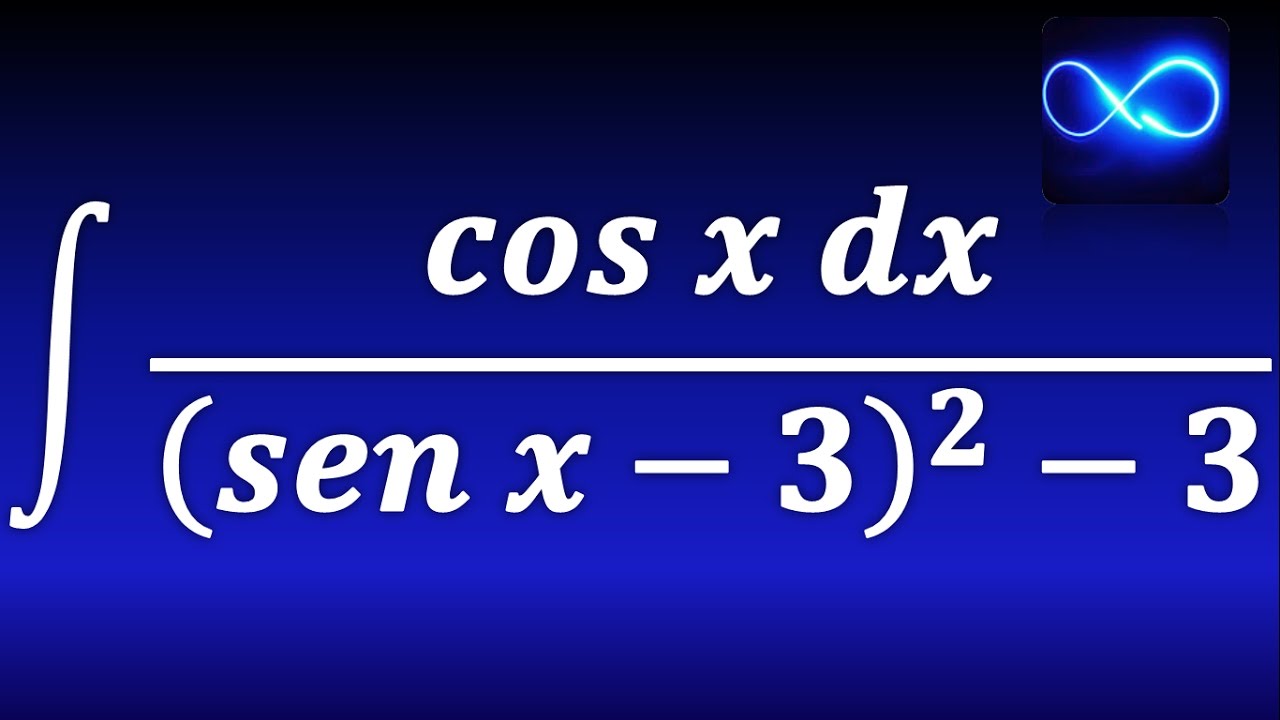
Integral de coseno entre seno cuadrado menos 3

Ley de cosenos para encontrar ángulo

Productos Notables. Binomio al Cuadrado.

DISTANCIA ENTRE DOS PUNTOS DEL PLANO: DEMOSTRACIÓN Y EJEMPLO

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera
5.0 / 5 (0 votes)