Fungsi Rasional Bentuk 1 (Domain, Range, Cara Menggambar)
Summary
TLDRThis video explains the concept of rational functions, focusing on their definitions, key features, and how to graph them. It covers topics such as identifying intercepts, vertical and horizontal asymptotes, domain and range, and provides step-by-step examples using specific functions. The presenter demonstrates how to calculate values for intercepts and asymptotes, offering insights on how to plot rational functions accurately. The video aims to make learning about rational functions, including linear and quadratic forms, accessible and practical for students studying algebra and pre-calculus.
Takeaways
- 😀 Rational functions map real numbers to rational numbers and are typically represented as the ratio of two polynomials (PX / GX).
- 😀 Polynomials can vary in degree, with simple examples like linear (ax + b) and quadratic (ax^2 + bx + c) polynomials.
- 😀 Graphing rational functions involves finding the x- and y-intercepts, vertical asymptotes, and horizontal asymptotes.
- 😀 Vertical asymptotes occur when the denominator of the function is zero, and the function approaches but never touches or crosses these lines.
- 😀 Horizontal asymptotes describe the behavior of the graph as it approaches infinity. They can be found by dividing the leading coefficients of the numerator and denominator.
- 😀 The domain of a rational function excludes the x-values that make the denominator zero (vertical asymptotes).
- 😀 The range of a rational function excludes the y-values that correspond to horizontal asymptotes.
- 😀 Step-by-step methods to graph rational functions involve calculating intercepts and determining asymptotes before sketching the curve.
- 😀 The rational function examples given include calculations for x- and y-intercepts and how to handle both vertical and horizontal asymptotes.
- 😀 When graphing, auxiliary points (e.g., for x = 2, x = 4, etc.) can help accurately depict the curve, especially for parts of the graph that are less clear.
- 😀 Asymptotes act as boundaries for the graph, meaning the curve approaches these lines but does not intersect them, ensuring accuracy in plotting.
Q & A
What is a rational function?
-A rational function is a function that maps a real number x to a rational number, typically expressed as the ratio of two polynomials, P(x) divided by Q(x), where both P(x) and Q(x) are polynomials.
What are the common forms of polynomials used in rational functions?
-Common forms of polynomials used in rational functions include linear polynomials (e.g., ax + b), quadratic polynomials (e.g., ax² + bx + c), cubic polynomials (e.g., ax³ + bx² + cx + d), and higher-degree polynomials.
How do you find the x-intercept of a rational function?
-The x-intercept is found by setting the numerator of the rational function equal to zero and solving for x. This gives the point(s) where the curve crosses the x-axis.
How do you find the y-intercept of a rational function?
-To find the y-intercept, substitute x = 0 into the function and solve for y. This gives the point where the curve crosses the y-axis.
What is a vertical asymptote, and how is it determined?
-A vertical asymptote is a boundary line that the curve approaches but never touches or crosses. It is determined by setting the denominator of the rational function equal to zero and solving for x.
What is a horizontal asymptote, and how is it determined?
-A horizontal asymptote is a line that the curve approaches as x tends to positive or negative infinity. It is found by taking the ratio of the leading coefficients of the numerator and denominator polynomials.
What does the domain of a rational function refer to?
-The domain of a rational function refers to the set of all possible x-values for which the function is defined, which excludes any values that cause division by zero (i.e., the values where the denominator is zero).
What is the range of a rational function?
-The range of a rational function refers to the set of all possible output values (y-values). The range excludes any values that the function cannot reach, such as those corresponding to horizontal asymptotes.
In the example 2x - 4 / (x - 3), what is the x-intercept?
-The x-intercept is found by setting the numerator 2x - 4 equal to zero. Solving for x gives x = 2, so the x-intercept is at (2, 0).
In the example 2x - 4 / (x - 3), what is the y-intercept?
-To find the y-intercept, substitute x = 0 into the function. This gives y = (2(0) - 4) / (0 - 3) = -4 / -3 = 4/3, so the y-intercept is at (0, 4/3).
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Relasi dan Fungsi Matematika Kelas 10 • Part 27: Soal Fungsi Rasional Bentuk 3 - Kuadrat / Linear
Relasi dan Fungsi Matematika Kelas 10 • Part 24: Fungsi Rasional Bentuk 2 - Linear / Kuadrat
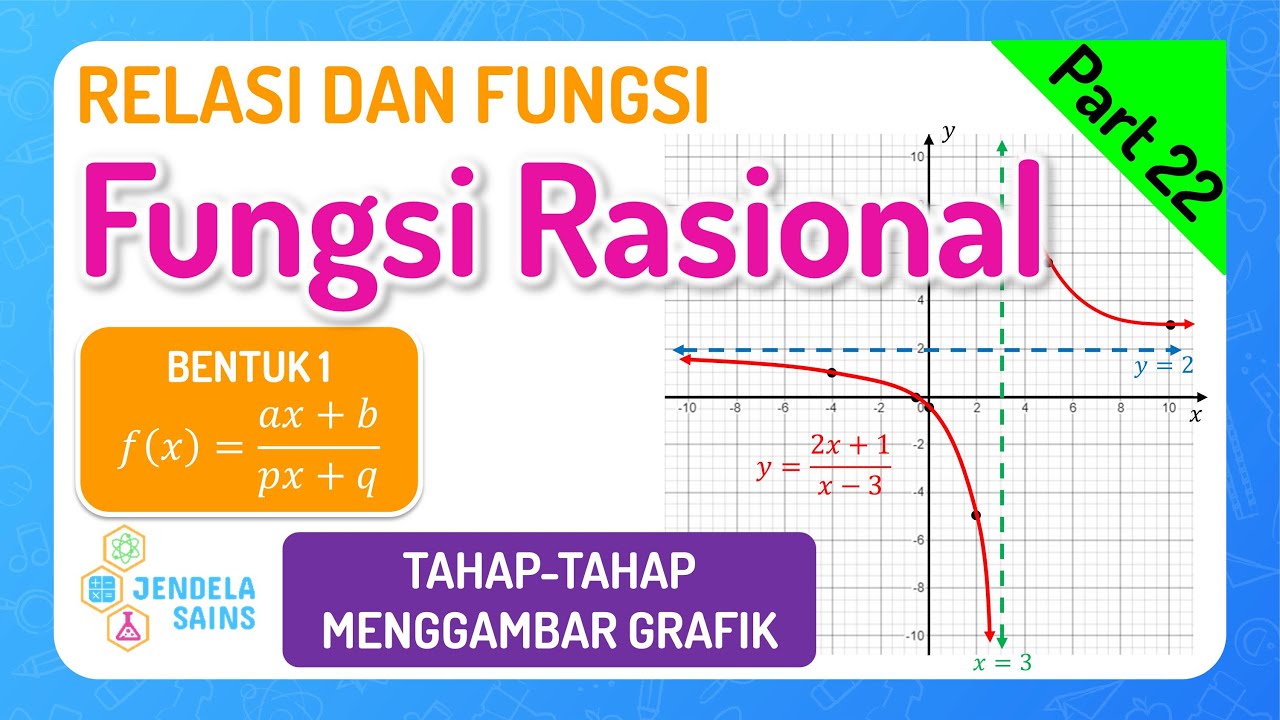
Relasi dan Fungsi Matematika Kelas 10 • Part 22: Fungsi Rasional Bentuk 1 - Linear / Linear

Relasi dan Fungsi Matematika Kelas 10 • Part 26: Fungsi Rasional Bentuk 3 - Kuadrat / Linear
Fungsi Rasional kelas XI Matematika Tingkat Lanjut (Kurikulum Merdeka)

Menyusun Rumus Fungsi Rasional #fazanugas
5.0 / 5 (0 votes)
