How To Convert From Slope Intercept Form to Standard Form | Algebra
Summary
TLDRIn this video, viewers are taught how to convert linear equations from slope-intercept form to standard form. The process is demonstrated step-by-step, with examples including equations with fractions. The key steps include moving the x and y terms to the left side, keeping the constant on the right, and adjusting signs as needed. The video also covers handling fractions by multiplying through by denominators to eliminate them. By following these steps, viewers can convert any linear equation into standard form, including those with fractions or negative signs.
Takeaways
- 😀 Convert a linear equation from slope-intercept form (y = mx + b) to standard form (Ax + By = C) by rearranging the terms.
- 😀 To convert from slope-intercept to standard form, move the x and y terms to the left side of the equation, keeping the constant on the right side.
- 😀 When moving terms from one side of the equation to the other, change the sign of the term (e.g., positive 3x becomes negative 3x).
- 😀 After rearranging, multiply by negative one to ensure the equation is in the correct format, i.e., Ax + By = C.
- 😀 For equations with fractions, multiply everything by the denominator to eliminate the fraction.
- 😀 When dealing with fractions, make sure to simplify by canceling out the denominators before proceeding with other steps.
- 😀 In equations with fractions, use multiplication to eliminate the fractions and convert the equation to a form that can be rearranged into standard form.
- 😀 If an equation involves negative signs, multiply the entire equation by negative one to make the coefficients positive.
- 😀 For more complex problems involving different fractions, find the least common denominator (LCD) to eliminate fractions in one step.
- 😀 In standard form, always ensure that the x term comes before the y term, and the constant is on the right side of the equation.
Q & A
What is the difference between slope-intercept form and standard form?
-Slope-intercept form is written as y = mx + b, where 'm' is the slope and 'b' is the y-intercept. Standard form is written as Ax + By = C, where 'A', 'B', and 'C' are integers, and 'A' should be positive if possible.
How do you convert an equation from slope-intercept form to standard form?
-To convert from slope-intercept form to standard form, move the 'x' and 'y' terms to the left side of the equation and the constant to the right. Then, multiply through by necessary factors to eliminate fractions and ensure integer coefficients.
In the example y = 3x - 4, what is the first step in converting it to standard form?
-The first step is to move the 3x term from the right side to the left side of the equation. This is done by subtracting 3x from both sides, resulting in -3x + y = -4.
Why do you multiply the equation by -1 in some cases?
-Multiplying by -1 is done to simplify the equation and avoid negative coefficients, especially for the 'y' term. It helps maintain consistency in standard form, where it's preferred to have positive coefficients for the 'x' term if possible.
How do you handle fractions in a slope-intercept equation?
-When fractions are present, you multiply both sides of the equation by the denominator of the fraction to eliminate it. For example, in y = (2/5)x + 3, you would multiply both sides by 5.
What happens when both the slope and the y-intercept are fractions with different denominators?
-In this case, you multiply both sides of the equation by the least common denominator (LCD) of the fractions' denominators. For example, if the fractions have denominators of 4 and 3, you would multiply everything by 12.
What is the importance of rearranging terms when converting to standard form?
-Rearranging the terms ensures the equation follows the standard form format, Ax + By = C. Specifically, the 'x' term should be first, followed by the 'y' term, and then the constant.
In the example y = 3/4x + 2/3, why is 12 chosen as the common multiple?
-12 is chosen because it is the least common denominator (LCD) of 4 and 3. By multiplying the entire equation by 12, we eliminate the fractions.
What is the final step after eliminating fractions and rearranging terms?
-The final step is to ensure the equation is in the form Ax + By = C, with integer coefficients. If necessary, multiply by -1 to avoid negative coefficients for 'x' or 'y'.
Can you provide an example of a situation where the standard form equation might need to be rewritten with a positive coefficient for 'x'?
-If the 'x' coefficient is negative, some teachers may prefer it to be positive in standard form. For example, -9x + 12y = -8 can be rewritten as 9x - 12y = 8 by multiplying the entire equation by -1.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Standard Form - Lesson 6.3
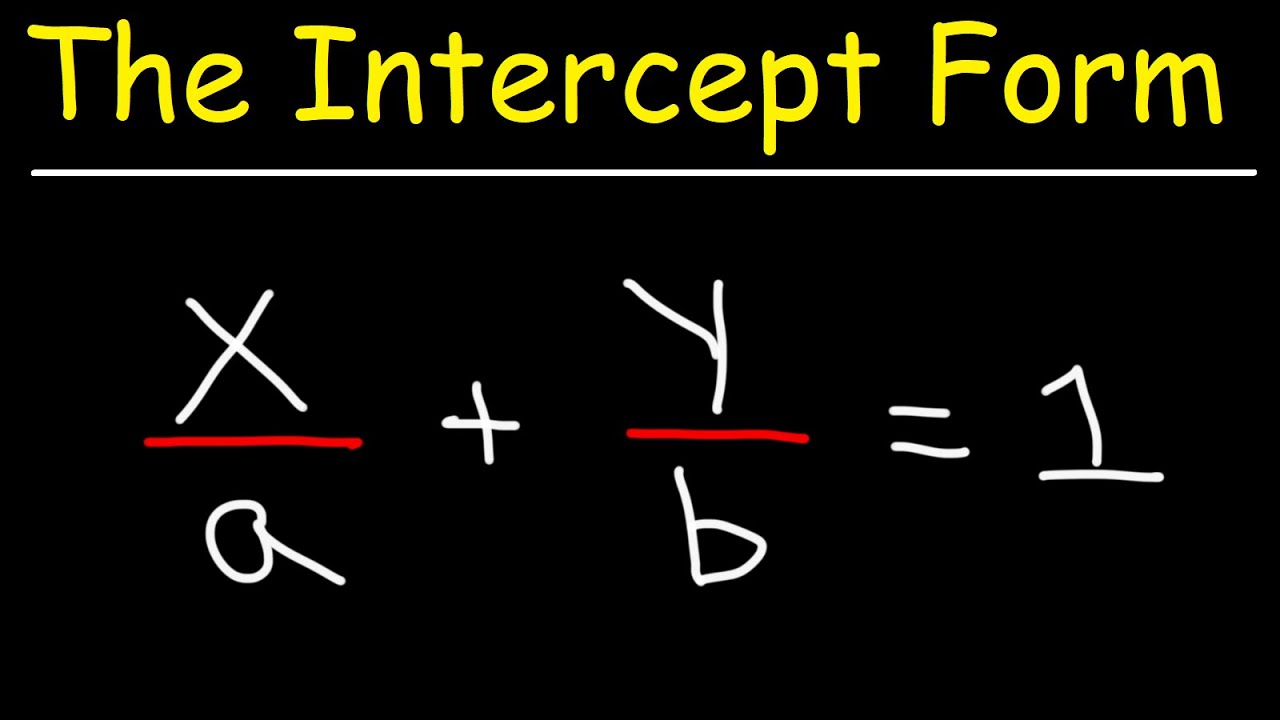
Linear Equations - The Intercept Form - Algebra

Grade 8 Lesson 2.2: Point Slope Form Short Video
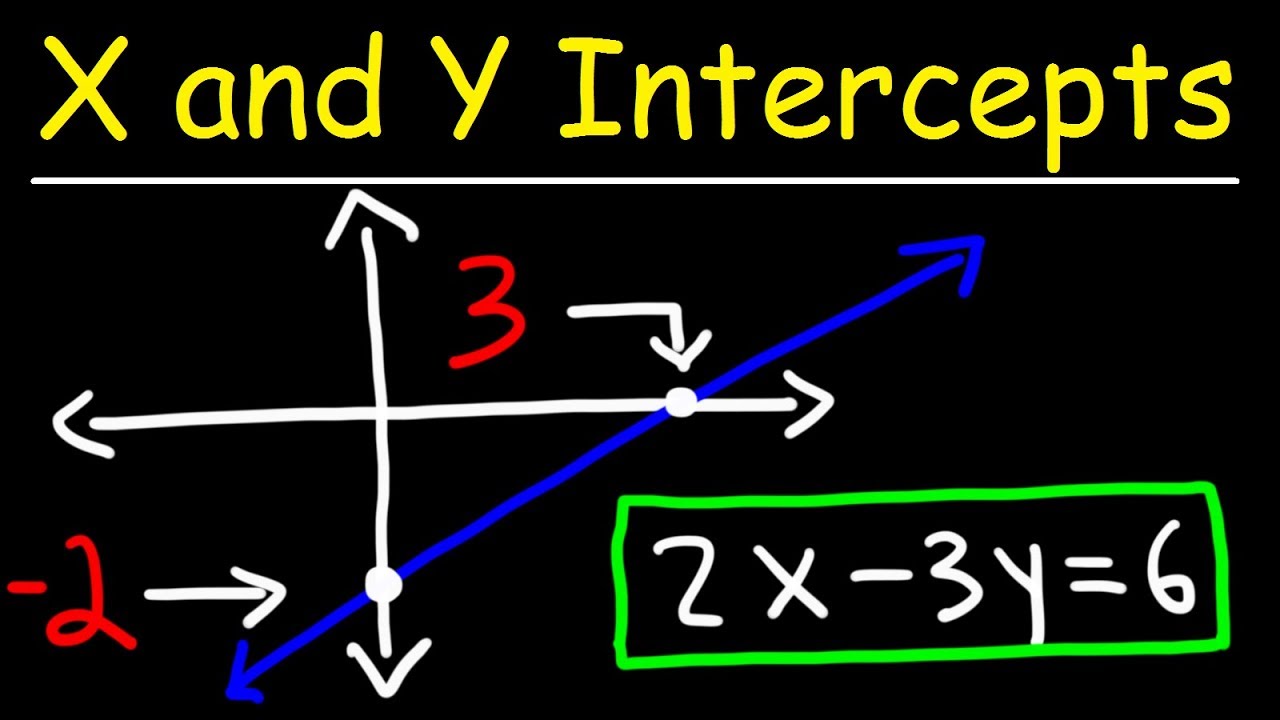
How To Find The X and Y Intercepts of a Line

FINDING THE EQUATION OF A LINE GIVEN THE X AND Y - INTERCEPTS || GRADE 8 MATHEMATICS Q1

Writing Equations of Parallel and Perpendicular Lines
5.0 / 5 (0 votes)
