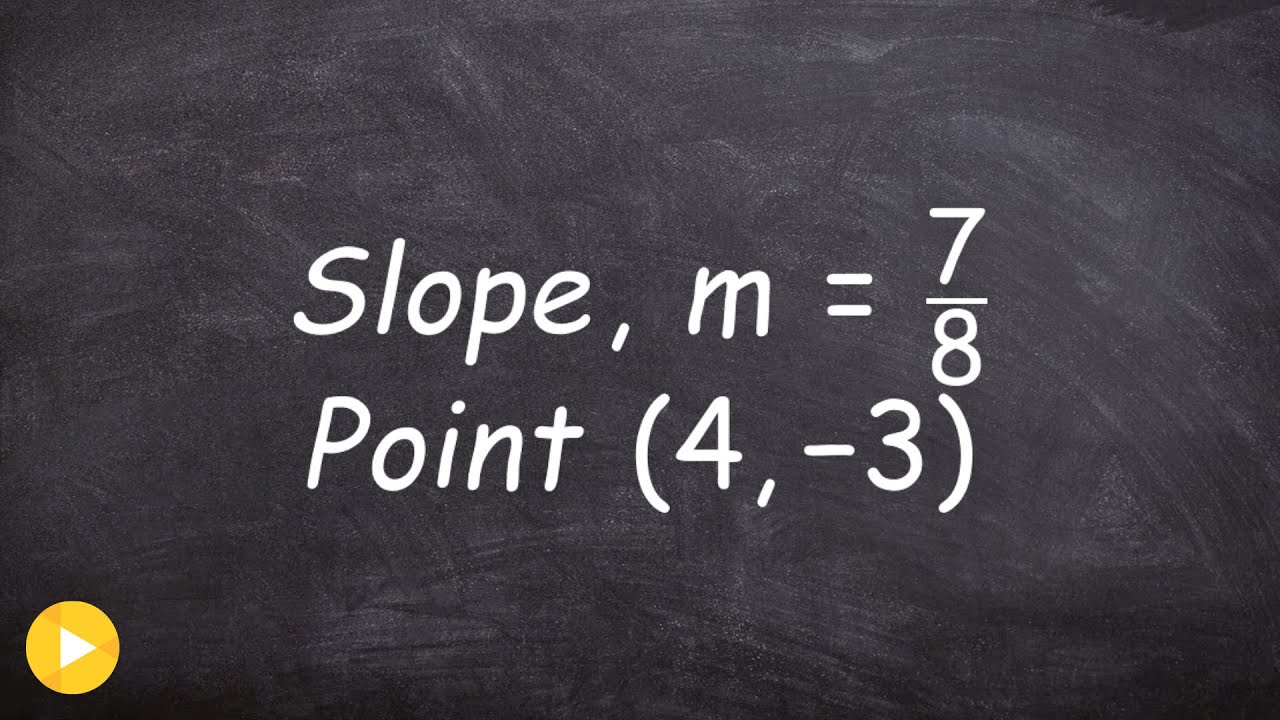Grade 8 Lesson 2.2: Point Slope Form Short Video
Summary
TLDRThis lesson explains different forms for writing the equation of a line, focusing on point-slope and slope-intercept forms. It covers the use of slope and points to find and write the equation, demonstrating how to work with a point and slope, two points, a table, and graphs. The video also highlights how to convert between point-slope form and slope-intercept form, and provides clear examples to reinforce understanding. Viewers are encouraged to practice with several examples to strengthen their grasp on writing and interpreting linear equations.
Takeaways
- 😀 The lesson focuses on understanding different forms of the equation of a line, specifically slope-intercept form and point-slope form.
- 😀 Slope-intercept form is useful when the slope (m) and the y-intercept (b) are known, and it simplifies the equation to y = mx + b.
- 😀 Point-slope form is used when a point (x1, y1) and the slope (m) are known, and it's written as y - y1 = m(x - x1).
- 😀 If given a point and slope, you can easily write the equation using point-slope form by substituting the values into the formula.
- 😀 When given two points, you can calculate the slope (m) using the formula (y2 - y1) / (x2 - x1) and then apply it to point-slope form.
- 😀 Tables with multiple points can be used to find a pair of points, and then you can follow the same steps as with two points to write the equation in point-slope form.
- 😀 For graphs, you can determine the slope by using the rise-over-run method, which involves counting vertical and horizontal distances between points on the line.
- 😀 To convert point-slope form to slope-intercept form, distribute the slope and simplify the equation to isolate y = mx + b.
- 😀 The lesson provides practice on using these forms in various scenarios, such as given points, a table, or a graph.
- 😀 When asked to graph an equation, first identify the point (x1, y1) from the equation, then use the slope to find additional points, and connect them to graph the line.
Q & A
What is the primary focus of the lesson in the script?
-The primary focus of the lesson is teaching different methods of writing the equation of a line, specifically using point-slope form and slope-intercept form.
What are the two key forms of equations discussed in the lesson?
-The two key forms discussed are the slope-intercept form (y = mx + b) and the point-slope form (y - y1 = m(x - x1)).
Why would someone prefer to use the point-slope form over the slope-intercept form?
-Point-slope form is preferred when you have a point (x1, y1) and a slope (m) and do not want to find the y-intercept (b).
What should you do if only two points are given, and you need to write the equation of the line in point-slope form?
-If only two points are given, first calculate the slope (m) using the formula (y2 - y1) / (x2 - x1), and then use the point-slope form with one of the points and the slope.
How can you calculate the slope if you are given a table of points?
-To calculate the slope from a table of points, select any two points and use the slope formula: m = (y2 - y1) / (x2 - x1).
What is the process to convert a point-slope form equation into the slope-intercept form?
-To convert from point-slope form to slope-intercept form, first distribute the slope (m) to the terms inside the parentheses, then isolate y to get the equation in the form y = mx + b.
What is the meaning of 'rise' and 'run' when calculating the slope?
-'Rise' refers to the vertical change (difference in y-values), and 'run' refers to the horizontal change (difference in x-values) between two points on the line.
How do you graph a line given the point-slope form of the equation?
-To graph a line from point-slope form, start at the point (x1, y1), then use the slope (rise/run) to find another point. Connect the points to graph the line.
What happens if you substitute 0 for x1 and y1 in the point-slope form?
-If you substitute 0 for both x1 and y1 in the point-slope form, the equation simplifies to the slope-intercept form, y = mx + b.
Why is it important to understand both the point-slope form and slope-intercept form?
-Understanding both forms allows for flexibility in solving problems, as some situations may give a point and slope (favoring point-slope form), while others may give the slope and y-intercept (favoring slope-intercept form).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)