Stress, Strain & Young's Modulus | A-level Physics | OCR, AQA, Edexcel
Summary
TLDRThis video explores the concepts of stress-strain graphs and Young's modulus, explaining their significance in understanding how materials respond to tensile forces. The script covers key points like the limit of proportionality, elastic and plastic behavior, yield points, ultimate tensile stress (UTS), and breaking stress. It also emphasizes the importance of stress-strain graphs, which are consistent across different objects made from the same material, and provides a detailed example of calculating Young's modulus. By the end, viewers gain a thorough understanding of material properties and their practical applications in physics.
Takeaways
- 😀 Stress-strain graphs are used to understand the behavior of materials under tensile force and provide important mechanical properties.
- 😀 A force-extension graph is material-specific and depends on the dimensions of the object being tested, making it different for each object even if made from the same material.
- 😀 Stress and strain are independent of a material's dimensions, making them more useful for analyzing material properties in a universal way.
- 😀 A stress-strain graph is the same for all objects made of the same material, regardless of their dimensions, allowing for consistent material behavior analysis.
- 😀 The stress-strain graph allows us to identify important properties like the limit of proportionality, elastic limit, and ultimate tensile stress (UTS).
- 😀 The limit of proportionality marks the point after which a material no longer follows Hooke's law and its stress and strain are no longer directly proportional.
- 😀 The elastic limit is the point at which a material will no longer return to its original shape after the load is removed, marking the transition from elastic to plastic behavior.
- 😀 Yield points (upper and lower) indicate sudden extensions in the material and a reduction in tensile stress between them.
- 😀 The ultimate tensile stress (UTS) represents the maximum tensile stress a material can withstand before necking occurs, and beyond this point, the material starts to weaken.
- 😀 Young's modulus is a measure of the stiffness of a material, calculated from the gradient of the linear region of the stress-strain graph, and it is unique to each material.
Q & A
What is the main purpose of a stress-strain graph?
-A stress-strain graph helps to investigate the behavior of a material under tensile stress, providing valuable insights into its mechanical properties, regardless of the material's original dimensions.
How can force-extension graphs be useful in studying materials?
-Force-extension graphs show the relationship between the force applied to a material and its extension. For example, they can be used to study a spring's behavior and confirm if it obeys Hooke's Law.
Why is a stress-strain graph more useful than a force-extension graph?
-A stress-strain graph is independent of the material's dimensions, making it more universally applicable to different objects made of the same material, unlike force-extension graphs which vary with dimensions.
What does 'stress' refer to in a stress-strain graph?
-Stress refers to the force applied to a material per unit area, usually measured in pascals (N/m²). It is represented on the y-axis of a stress-strain graph.
How is 'strain' defined in a stress-strain graph?
-Strain is the ratio of the extension of a material to its original length, and it has no units. It is represented on the x-axis of a stress-strain graph.
What is the 'limit of proportionality' on a stress-strain graph?
-The limit of proportionality is the point on a stress-strain graph where the relationship between stress and strain stops being linear, indicating that the material no longer obeys Hooke's Law.
What happens to a material when it exceeds the elastic limit?
-When a material exceeds its elastic limit, it begins to deform plastically, meaning it will not return to its original shape once the force is removed.
What is the difference between the upper and lower yield points on a stress-strain graph?
-The upper yield point is the peak of a small hump where the material first begins to undergo plastic deformation. The lower yield point is the point where the material's tensile stress drops, and strain continues to increase.
What does 'necking' refer to in a stress-strain graph?
-Necking is the phenomenon where a material, after reaching its ultimate tensile stress (UTS), becomes thinner and narrower at its weakest points before breaking.
How is Young's Modulus calculated from a stress-strain graph?
-Young's Modulus is calculated by finding the gradient of the linear portion of the stress-strain graph, which represents the ratio of tensile stress to tensile strain.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
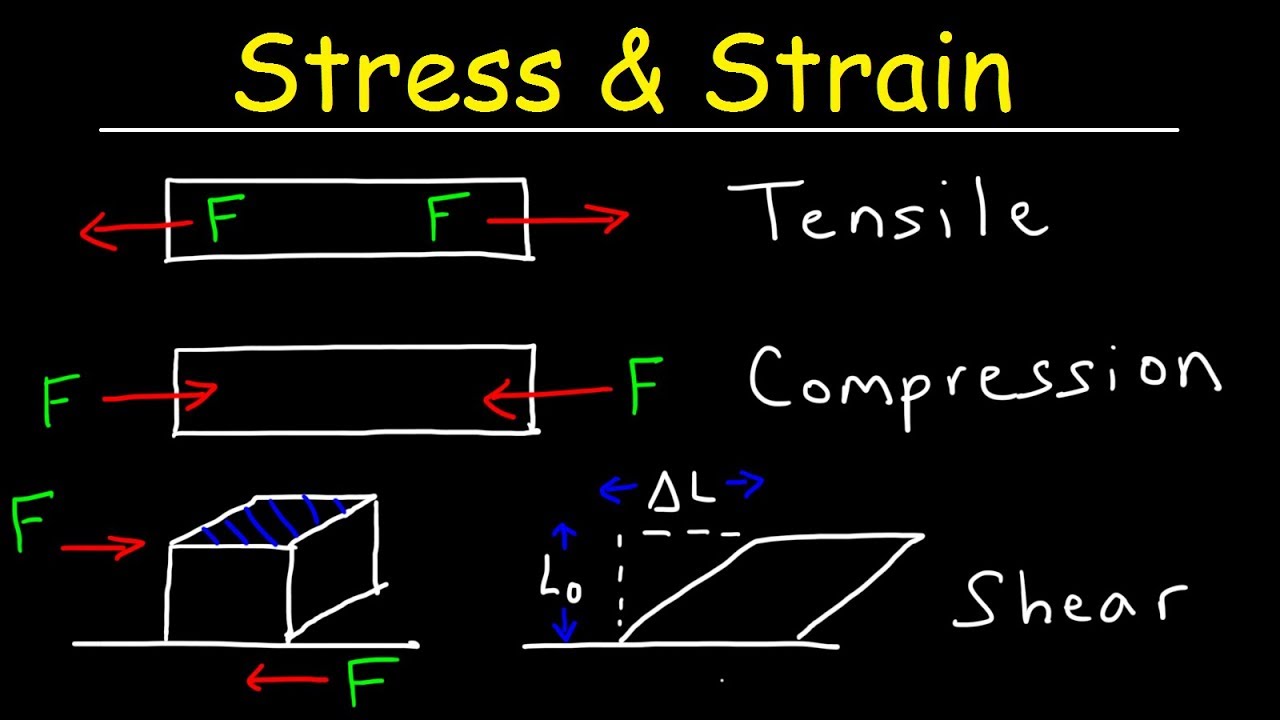
Tensile Stress & Strain, Compressive Stress & Shear Stress - Basic Introduction

Understanding Young's Modulus

Airframes & Aircraft Systems #1 - Aircraft Structures - Loads Applied to the Airframe
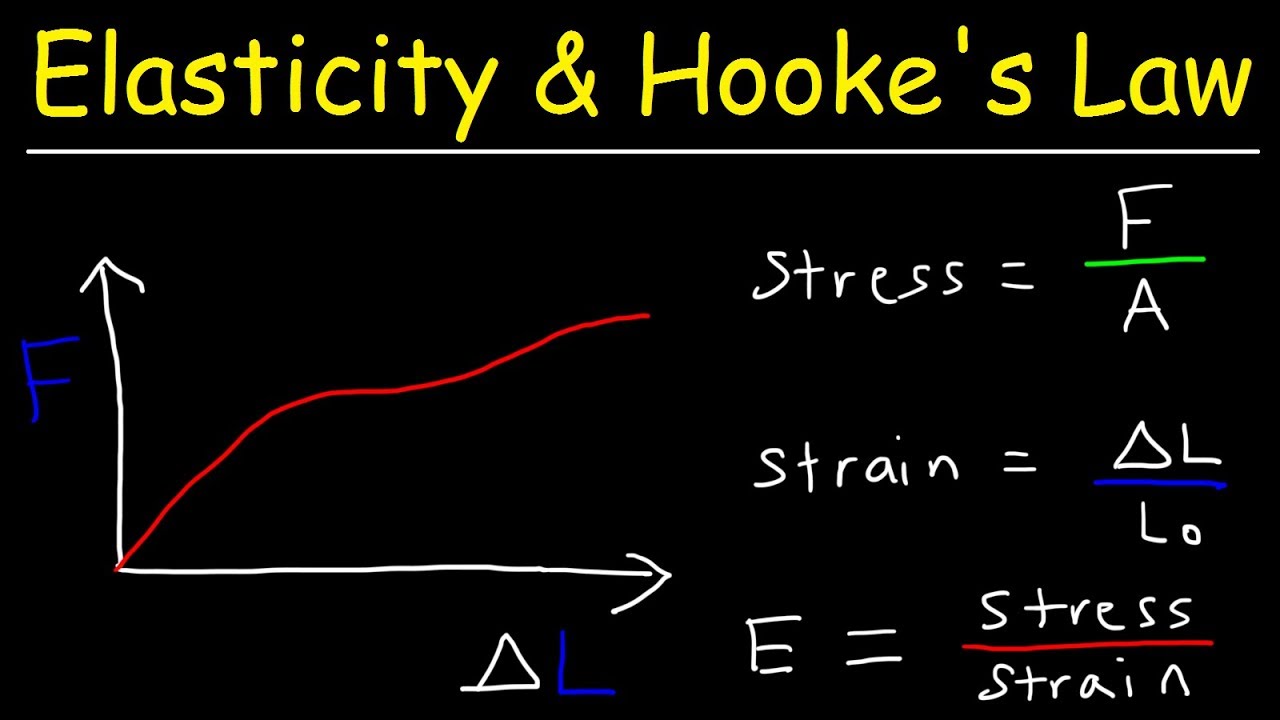
Elasticity & Hooke's Law - Intro to Young's Modulus, Stress & Strain, Elastic & Proportional Limit

Thermal Stresses And Strain in Hindi || Thermal Stress kya hoti hai

Stress and Strain | Stress strain curve of mild steel | Mechanical Properties of Solids |
5.0 / 5 (0 votes)
