Waagerechter Wurf | Wurfzeit und Wurfweite
Summary
TLDRIn this video, the presenter explores the physics behind horizontal projectile motion using the example of watering plants. By breaking down the movement of water droplets into horizontal and vertical components, the video explains how to calculate the time and distance of the throw. Through derived formulas, viewers learn that throw time is independent of horizontal speed, while throw distance depends on initial velocity and height. A practical example demonstrates how these principles can be applied to water hoses, making the concepts both educational and relatable for everyday life.
Takeaways
- 😀 The video explains horizontal projectile motion using the metaphor of watering flowers with a watering can.
- 😀 The water droplets follow a parabolic trajectory, with motion in both horizontal (x) and vertical (y) directions.
- 😀 The motion in the horizontal and vertical directions is independent and follows the principle of superposition.
- 😀 The vertical motion can be described using a time-position equation, and the horizontal motion uses a time-velocity equation.
- 😀 The time of flight (Wurfzeit) is independent of the initial horizontal velocity and only depends on the initial height and gravity.
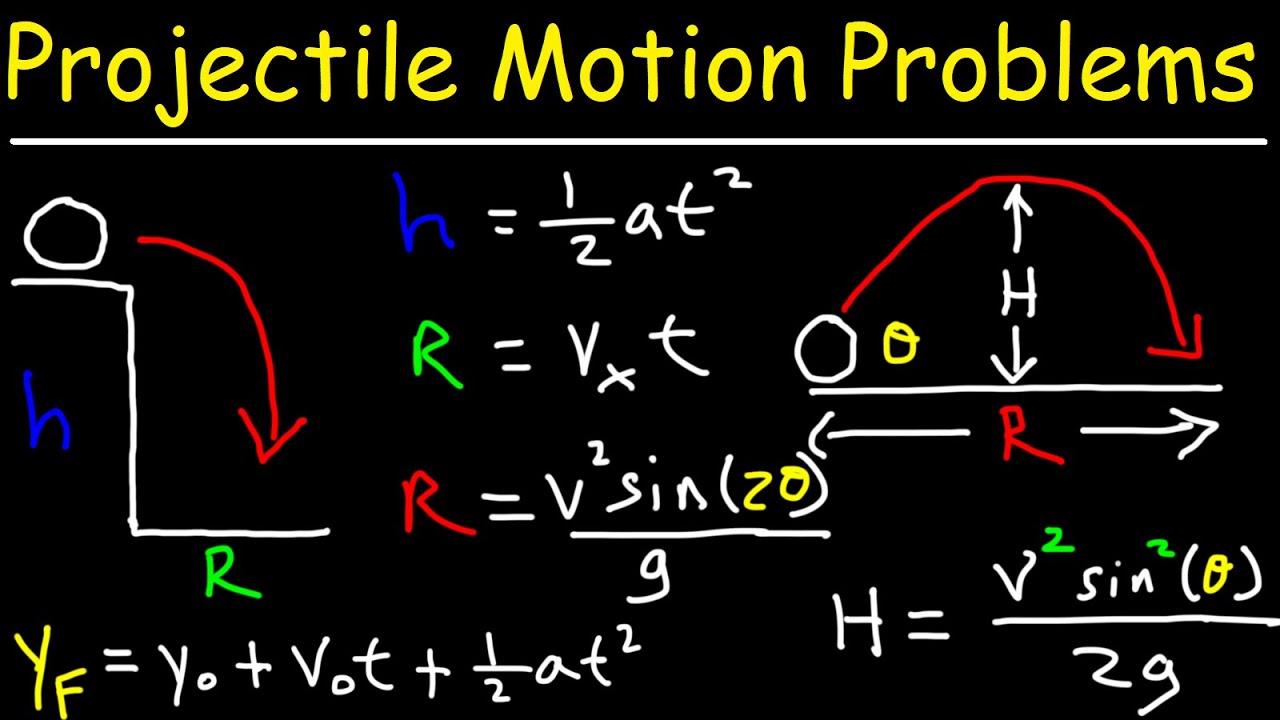
- 😀 The formula for the time of flight (Wurfzeit) is given by: T_W = √(2h/g), where h is the height and g is the gravitational acceleration.
- 😀 The horizontal distance (Wurfweite) a droplet travels is given by: W = V_0 * √(2h/g), where V_0 is the initial horizontal velocity.
- 😀 The time of flight is the same for droplets with different horizontal velocities, as long as they start at the same height.
- 😀 The horizontal distance traveled by the droplet increases with the initial velocity and the time it spends in the air.
- 😀 The example of watering flowers from a reclining position illustrates how the formulas can be applied to everyday situations, with a practical result showing the distance the water droplets travel.
Q & A
What is the basic concept of horizontal projectile motion discussed in the video?
-The basic concept is that the water droplet, like any object in horizontal projectile motion, has two independent components of motion: one in the horizontal (x) direction and one in the vertical (y) direction. These movements are governed by the principles of superposition, meaning they occur independently but combine to form the total trajectory.
What analogy does the speaker use to explain horizontal projectile motion?
-The speaker uses the analogy of watering flowers with a watering can. The water jet follows a curved path, which can be broken down into horizontal and vertical motion components, much like a projectile.
What mathematical principle helps in understanding the motion of a water droplet?
-The Superposition Principle is key in understanding the droplet's motion. It states that the horizontal and vertical motions of the droplet are independent and can be analyzed separately.
How does the speaker describe the components of the water's movement?
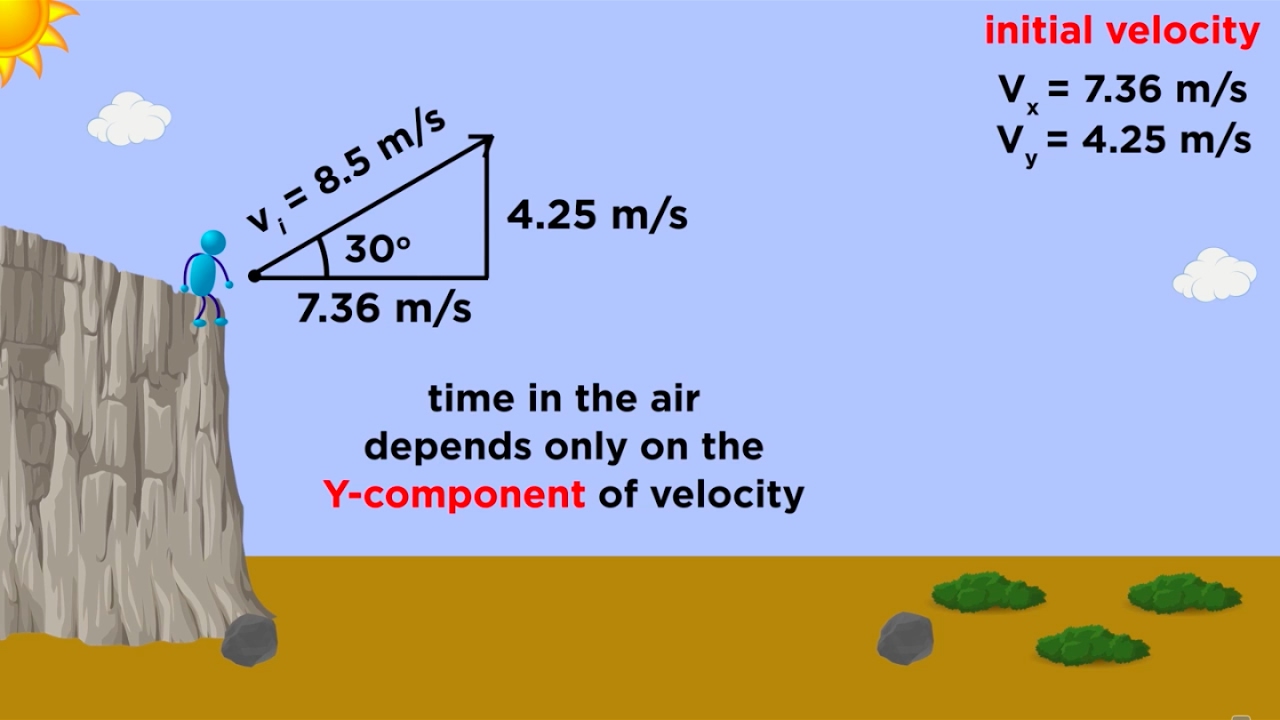
-The movement of the water droplet is described as having two components: the horizontal (x) direction, which is how far the droplet travels, and the vertical (y) direction, which describes the height of the droplet at any given point in time.
What is the formula for calculating the time of flight (Wurfzeit, TW) of the water droplet?
-The formula for the time of flight is TW = √(2h / g), where 'h' is the initial height from which the droplet is released and 'g' is the acceleration due to gravity.
What does the formula for Wurfzeit reveal about the motion of the droplet?
-The formula for Wurfzeit shows that the time of flight is independent of the horizontal speed of the water droplet. The time is solely determined by the height from which it is released and the gravitational acceleration.
How is the horizontal distance (Wurfweite, W) of the water droplet calculated?
-The horizontal distance, or Wurfweite, is calculated using the formula W = v0 * TW, where 'v0' is the initial velocity of the droplet and 'TW' is the time of flight. The Wurfzeit (TW) is substituted into the formula as √(2h / g).
How does the speaker use real-world numbers to apply the formula for Wurfweite?
-The speaker uses the example of watering flowers with a hose. The initial velocity (v0) is given as 16 m/s, and the initial height (h) is 40 cm. Plugging these values into the formula, the calculated Wurfweite is approximately 4.5 meters.
What does the speaker mean by 'Superposition' in the context of physics?
-In physics, 'Superposition' refers to the principle that independent movements or forces, like the horizontal and vertical motions of the droplet, can be analyzed separately but will combine to produce the overall result.
What practical purpose does the speaker have in mind when applying this physics concept?
-The speaker humorously discusses optimizing the process of watering flowers while lying on a chair, using the physics of horizontal projectile motion to calculate how far the water will travel when using the hose.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)