Introduction to Kinetic Energy with Example Problem
Summary
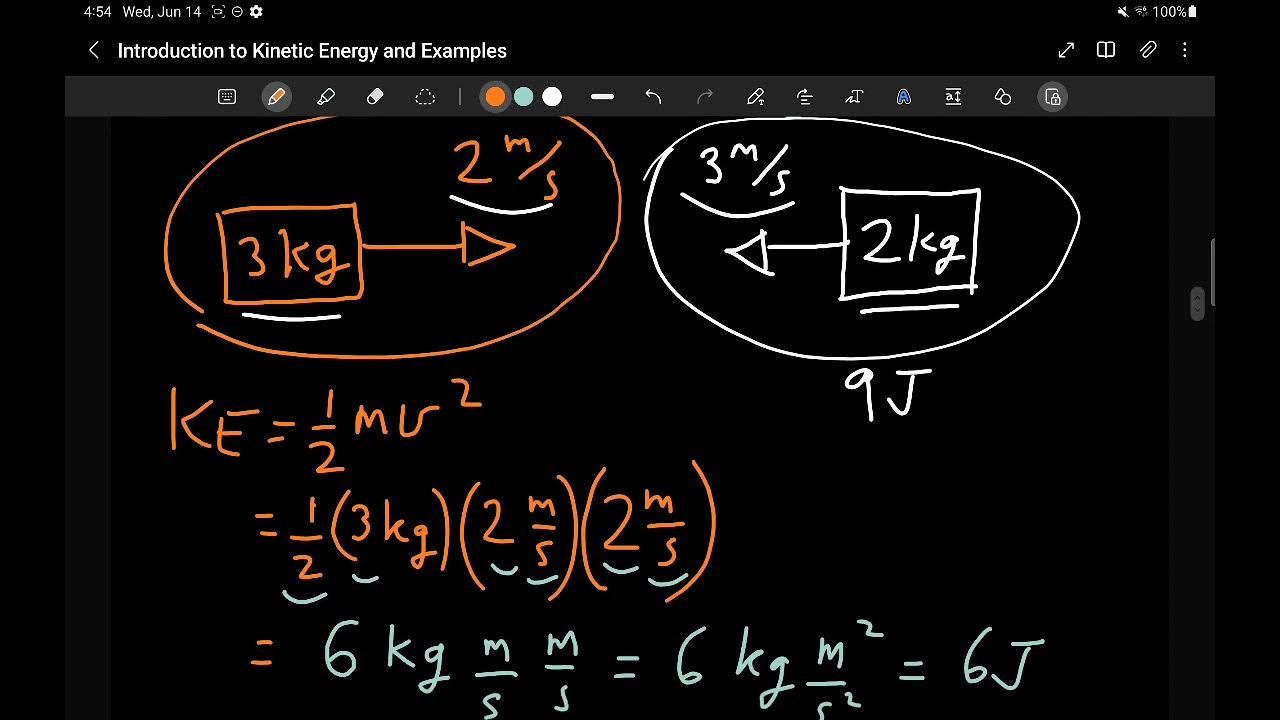
TLDRThis lesson introduces the concept of kinetic energy, explaining that it is the energy associated with an object's motion, represented by the formula KE = 1/2 mv². The video covers key concepts like the units of kinetic energy (joules), and the fact that it can never be negative since velocity is squared. A practical example is provided where the kinetic energy of a bike moving at 25 mph is compared to that of a Prius. The mass of both objects is used to calculate the speed of the Prius, illustrating the relationship between mass, velocity, and kinetic energy.
Takeaways
- 😀 Kinetic energy is the energy associated with the motion of an object.
- 😀 The formula for kinetic energy is KE = 1/2 mv², where 'm' is mass and 'v' is velocity.
- 😀 Kinetic energy is measured in joules, which are equivalent to kg·m²/s².
- 😀 Mass is always positive, but velocity can be negative, though kinetic energy can never be negative because velocity is squared in the formula.
- 😀 Kinetic energy is a scalar quantity, meaning it has magnitude but no direction.
- 😀 To solve kinetic energy problems, it's important to match the kinetic energies of the objects in question.
- 😀 In practical examples, the mass of the objects involved must be considered when comparing their kinetic energies.
- 😀 When comparing kinetic energy between two objects, the speed of the objects is key, but the velocity is the important term in the equation.
- 😀 For a bike and a Prius to have equal kinetic energy, their masses and velocities must be taken into account using the kinetic energy formula.
- 😀 In the example, the mass of the bike is 86 kg, and the mass of the Prius is 1,400 kg, leading to the Prius needing to travel at 6 mph to match the bike's kinetic energy.
- 😀 Units of measurement like mass in kilograms and velocity in meters per second are essential for calculating kinetic energy, and conversion may be necessary for consistent units.
Q & A
What does the word 'kinetic' mean in the context of the video?
-In the context of the video, 'kinetic' refers to anything related to motion, such as kinetic friction, which involves the motion of surfaces in contact.
What is the equation for kinetic energy?
-The equation for kinetic energy is KE = 1/2 mv², where 'm' represents the mass of the object and 'v' represents the velocity of the object.
What are the units for kinetic energy?
-The units for kinetic energy are joules. This is derived from the fact that mass is measured in kilograms, and velocity is measured in meters per second, leading to units of kilograms times meters squared per seconds squared, which is equivalent to joules.
Why can't kinetic energy ever be negative?
-Kinetic energy can't be negative because the velocity in the equation is squared, and the square of any number, positive or negative, is always positive. Additionally, mass itself cannot be negative.
Is kinetic energy a vector or a scalar?
-Kinetic energy is a scalar quantity, meaning it only has magnitude and no direction, unlike vectors which have both magnitude and direction.
How do you determine the velocity of a Prius if its kinetic energy equals that of a bike?
-To find the velocity of the Prius, you set the kinetic energy of the bike equal to the kinetic energy of the Prius, using the formula KE = 1/2 mv² for both objects. By rearranging and solving the equation, you can determine the velocity of the Prius, considering their respective masses.
Why don't we need the velocity of the bike when solving for the Prius's speed?
-We only need the magnitude of the velocity of the bike, as velocity is squared in the kinetic energy equation. This means that the direction doesn't affect the result, so we can use the bike's speed directly.
What mistake did the students initially make when solving for the Prius's speed?
-The students initially incorrectly canceled out the masses in the equation, not realizing that the masses for the bike and Prius are different. Each object’s mass should be considered separately in the equation.
Why did the students not need to convert the bike's speed from miles per hour to meters per second?
-The units of miles per hour are not converted because when solving for the velocity of the Prius, the mass terms cancel out, and the result only depends on the ratio of the masses. Therefore, the conversion is not necessary for this particular calculation.
What did the students learn about significant figures in the final answer?
-The students learned that the answer should be reported with the correct number of significant figures. However, since the Prius’s speedometer doesn't display decimal places, the final speed was rounded to a whole number, 6 miles per hour.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)