Comprimento de um Arco
Summary
TLDRThis tutorial explains how to calculate the length of an arc in a circle using two methods. The first method involves applying the formula: Arc Length = (Angle × π × Radius) / 180°, demonstrating how to find the arc length when given a 30° angle and a 10 cm radius. The second method uses the total circumference of the circle, calculated with the formula Circumference = 2π × Radius, and then sets up a proportion to find the arc length. Both methods yield the same result, with the arc length being approximately 5.23 cm. This video makes understanding arc length easy with clear, step-by-step calculations.
Takeaways
- 😀 An arc is a portion of a circle's circumference.
- 😀 To calculate the length of an arc, you need the radius and the central angle of the arc.
- 😀 The formula for calculating arc length is: Arc Length = (θ × π × r) / 180, where θ is the angle, π is approximately 3.14, and r is the radius.
- 😀 The angle (θ) is measured in degrees when using the arc length formula.
- 😀 A practical example shows how to calculate an arc length: For a 30° angle and a 10 cm radius, the length of the arc is approximately 5.23 cm.
- 😀 In the second method, first calculate the full circumference of the circle using the formula: Circumference = 2 × π × r.
- 😀 Once the full circumference is found, use a proportion to find the length of the arc based on the central angle.
- 😀 The proportion for calculating arc length is: Circumference / 360 = Arc Length / Angle.
- 😀 Using the second method, if the radius is 10 cm and the angle is 90°, the arc length is calculated to be 15.7 cm.
- 😀 The second method provides a way to find the arc length by understanding how the arc relates to the full circle's 360°.
- 😀 Both methods for calculating arc length (formula or proportion) are useful depending on the given problem or preference.
Q & A
What is an arc in geometry?
-An arc is a segment of the circumference of a circle. It is defined by two points on the circle, with the portion between them forming the arc.
What is the formula for calculating the length of an arc?
-The formula for calculating the length of an arc is: L = (θ / 180°) × π × r, where L is the length of the arc, θ is the central angle in degrees, π is approximately 3.14, and r is the radius of the circle.
How is the length of the arc related to the angle of the arc?
-The length of the arc is directly proportional to the central angle of the arc. As the angle increases, the length of the arc increases.
Why is π approximately equal to 3.14 used in the calculations?
-π is an irrational number that represents the ratio of the circumference of a circle to its diameter. In most practical problems, it is approximated as 3.14 for ease of calculation.
What is the first method described for calculating the arc length in the script?
-The first method involves using the formula for the arc length: L = (θ / 180°) × π × r, where θ is the central angle and r is the radius of the circle.
How does simplifying the fraction 30/180 help in solving the problem?
-Simplifying 30/180 to 1/6 makes the calculation easier by reducing the numbers involved, simplifying the process and reducing the chance of error.
What is the second method used to find the arc length in the script?
-The second method involves first calculating the circumference of the circle using the formula C = 2 × π × r, and then applying a rule of three to find the length of the arc based on its corresponding central angle.
What is the rule of three used for in the second method?
-The rule of three is used to set up a proportion between the full circumference (360°) and the arc corresponding to a specific angle, helping to find the arc length.
How is the circumference of a circle calculated?
-The circumference of a circle is calculated using the formula C = 2 × π × r, where C is the circumference and r is the radius of the circle.
In the example, what was the radius and the resulting arc length for a 30° angle?
-In the example, the radius was 10 cm, and using the first method, the arc length for a 30° angle was calculated to be approximately 5.23 cm.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Cara Menghitung Panjang Busur dan Luas Juring Lingkaran
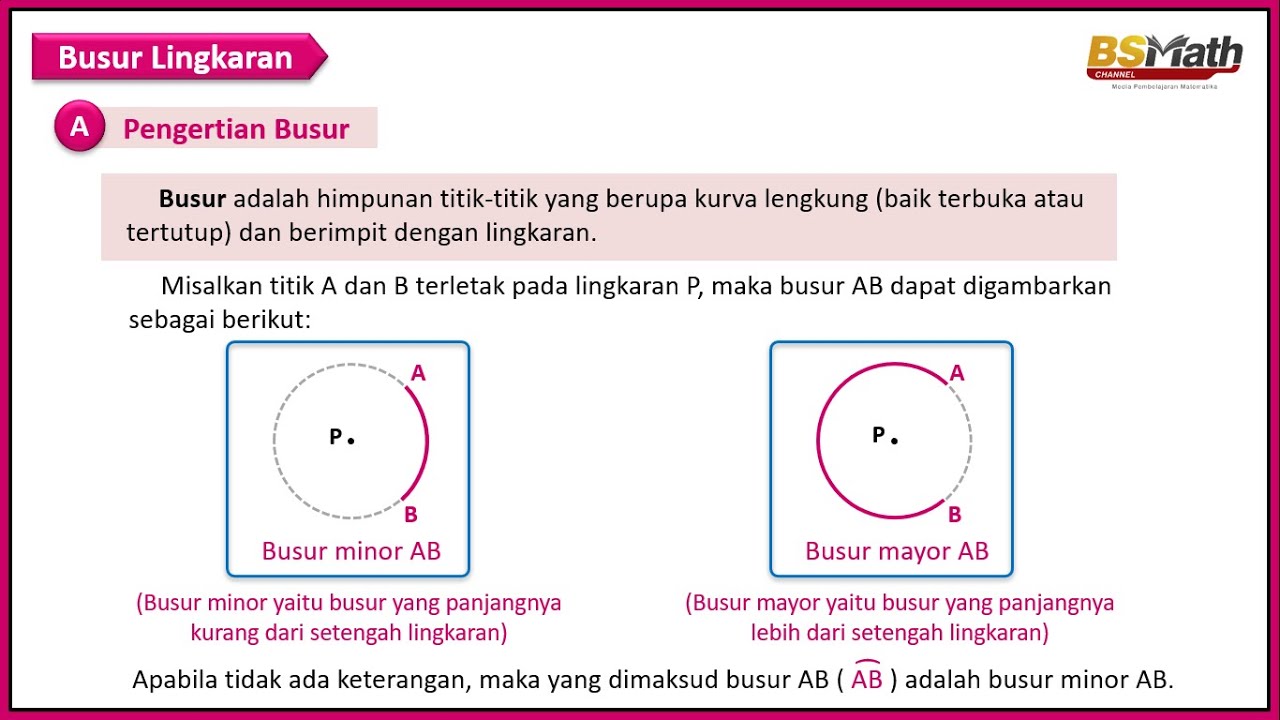
Busur Lingkaran | Matematika SMA Kelas XI Kurikulum Merdeka
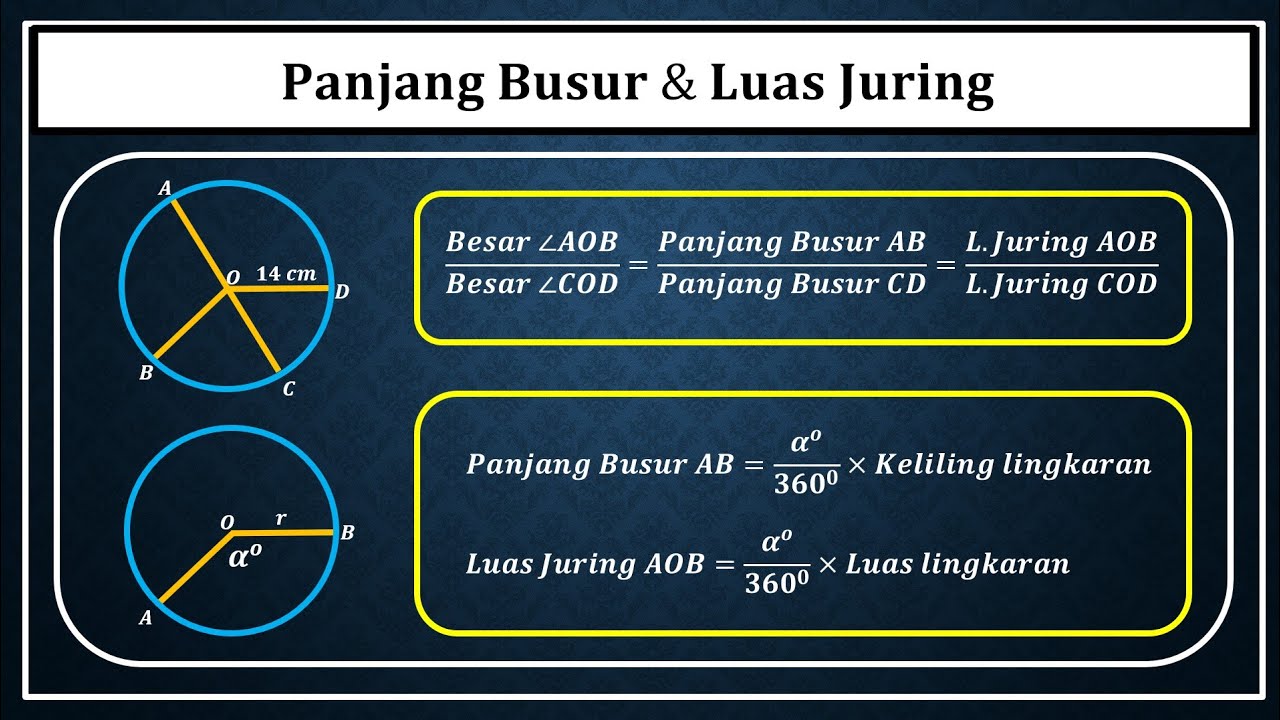
Panjang Busur dan Luas Juring Lingkaran
Pre-Calculus 12 - Video #25: Trigonometric Basics

Lingkaran [Part 3] - Panjang Busur dan Luas Juring
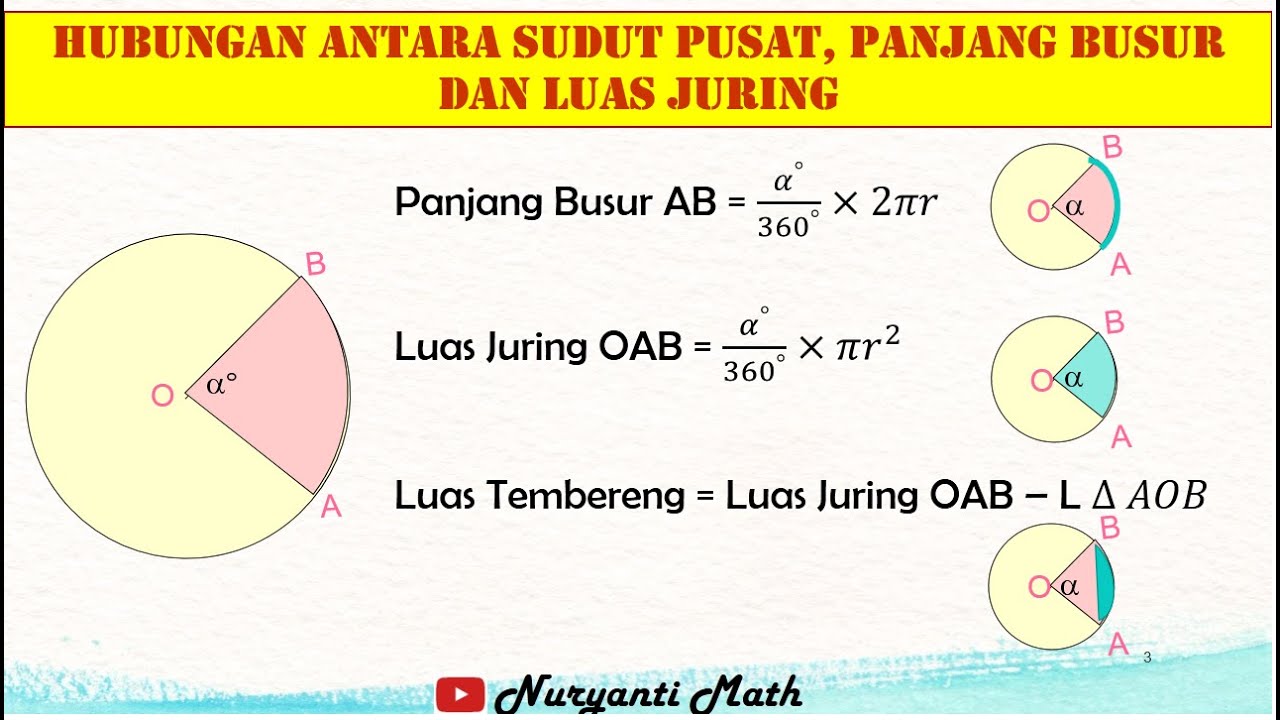
Hubungan antara Sudut Pusat, Panjang Busur dan Luas Juring
5.0 / 5 (0 votes)
