Ecuación canónica o simétrica de la recta
Summary
TLDREn este video, se explica de manera clara la ecuación canónica o simétrica de la recta, abordando conceptos fundamentales como la abscisa y la ordenada en el origen. A través de ejemplos prácticos, se muestra cómo graficar rectas usando esta ecuación, ubicando los puntos de corte con los ejes X y Y. Además, se detallan situaciones con signos negativos en la ecuación, y cómo afectan al gráfico. El video invita a los estudiantes a explorar más sobre el tema en un curso completo disponible en el canal, y a interactuar con el contenido mediante comentarios y suscripciones.
Takeaways
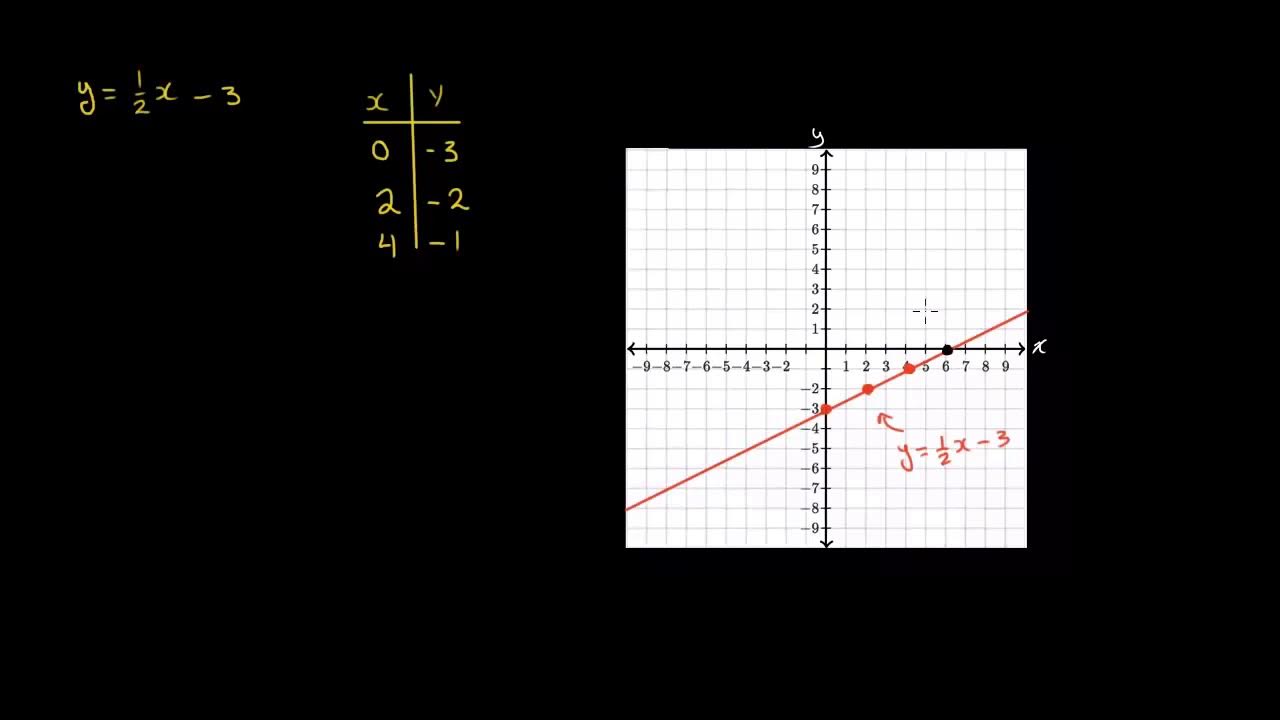
- 😀 La ecuación canónica o simétrica de la recta tiene la forma: x/a + y/b = 1.
- 😀 La 'a' representa la abscisa en el origen, es decir, el punto de corte con el eje x.
- 😀 La 'b' representa la ordenada en el origen, es decir, el punto de corte con el eje y.
- 😀 Un beneficio de la ecuación canónica es que es fácil de graficar identificando directamente los puntos de corte con los ejes.
- 😀 En la ecuación x/3 + y/5 = 1, el punto de corte con el eje x es 3 y el punto de corte con el eje y es 5.
- 😀 Para graficar, solo se necesitan los puntos de corte con los ejes x y y, y luego trazar la recta.
- 😀 Si la ecuación contiene valores negativos, estos indican que los puntos de corte están en el lado opuesto de los ejes.
- 😀 En el caso de la ecuación x/3 - y/4 = 1, la abscisa sigue siendo 3, pero la ordenada es -4, lo que indica un corte debajo del eje y.
- 😀 La ecuación puede ser reescrita para facilitar su interpretación, por ejemplo, transformando el signo negativo en el denominador.
- 😀 La visualización de los puntos de corte es clave para graficar correctamente la recta en un plano cartesiano.
- 😀 Se recomienda practicar con diferentes valores de los coeficientes para comprender bien cómo afectan la posición de la recta en el plano.
Q & A
¿Qué es la ecuación canónica o simétrica de la recta?
-Es una forma de representar la ecuación de la recta en la que se utilizan las abscisas y ordenadas en el origen para definir el punto de corte de la recta con los ejes X y Y respectivamente.
¿Qué representa la 'a' en la ecuación canónica de la recta?
-La 'a' representa la abscisa en el origen, es decir, el punto donde la recta corta el eje X.
¿Qué significa la 'b' en la ecuación canónica de la recta?
-La 'b' representa la ordenada en el origen, es decir, el punto donde la recta corta el eje Y.
¿Cómo se puede graficar una recta usando la ecuación canónica?
-Para graficar una recta con la ecuación canónica, se deben ubicar los puntos de corte con el eje X y el eje Y, luego conectar estos puntos para formar la recta.
¿Qué sucede si los valores de los puntos de corte son negativos?
-Si los valores son negativos, los puntos de corte con los ejes X o Y se ubican en la dirección opuesta, es decir, hacia la izquierda en el eje X o hacia abajo en el eje Y.
¿Cuál es el beneficio de usar la ecuación canónica para graficar?
-El beneficio principal es que es una de las ecuaciones más fáciles de graficar, ya que solo se necesita identificar los puntos de corte con los ejes X y Y.
¿Qué representa el signo negativo en la ecuación canónica?
-El signo negativo indica que uno de los puntos de corte está en una posición opuesta al origen, por ejemplo, un punto de corte negativo en el eje Y estaría por debajo del eje X.
¿Cómo se modificaría la ecuación si el valor de uno de los puntos de corte es negativo?
-Si uno de los valores es negativo, simplemente se refleja la posición del punto de corte sobre el eje correspondiente, ya sea X o Y, sin cambiar el resto de la ecuación.
¿Qué significa que la ecuación esté escrita de la forma 'x sobre 3 + y sobre 5 = 1'?
-Esta forma significa que la recta corta el eje X en el punto 3 y el eje Y en el punto 5. Al graficar, se ubicará un punto en el eje X en 3 y un punto en el eje Y en 5.
¿Cómo se podría graficar la ecuación 'x sobre 3 - y sobre 4 = 1'?
-Para graficar esta ecuación, primero se identificaría el punto de corte en el eje X (3) y el punto de corte en el eje Y (-4), ubicando estos puntos en el plano cartesiano y trazando la recta que los conecta.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Ecuaciones de la recta y sus transformaciones

Tipos de rectas: Horizontal, vertical e inclinada

Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)
Introducción a las intersecciones con los ejes

HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE
Ecuación general de la recta
5.0 / 5 (0 votes)
