Projectile Motion Launched at an Angle | Height and Range | Grade 9 Science Quarter 4 Week 2
Summary
TLDRThis engaging lesson from Maestrang Techy's YouTube channel dives into the intricacies of projectile motion launched at an angle. The video begins by revisiting the fundamental concepts of projectile motion, emphasizing the parabolic trajectory and the distinction between constant horizontal velocity and vertical acceleration due to gravity. The focus then shifts to the impact of the angle of release on a projectile's range and height. The channel illustrates that a 45-degree launch angle yields the maximum range, while a 75-degree angle results in the greatest height. The lesson is enriched with real-world examples, such as a baseball game, to contextualize the theory. Mathematical equations are introduced to solve for variables like maximum height and horizontal displacement, demonstrated through a practical problem involving a baseball hit at a 25-degree angle. The video concludes with a call to action, encouraging viewers to engage with the content and anticipate future lessons, making it an informative and interactive learning experience.
Takeaways
- 📚 The lesson focuses on the projectile motion launched at an angle, exploring the relationship between the angle of release and the height and range of the projectile.
- 🚀 Projectile motion involves a parabolic trajectory with horizontal and vertical components; the horizontal component has constant velocity, while the vertical has constant acceleration due to gravity (9.8 m/s²).
- 🌟 The vertical velocity of a projectile changes throughout its trajectory: it decreases as the projectile rises due to gravity, becomes zero at the highest point, and increases as it falls back down due to the direction aligning with gravity.
- 🏐 The game of baseball serves as an example of projectile motion launched at an angle, where the horizontal velocity (Vx) remains constant, and the vertical velocity (Vy) changes as described.
- 📐 When launching a projectile at an angle, the initial velocity can be resolved into horizontal and vertical components, with the horizontal velocity being constant and the vertical velocity affected by gravity.
- ⏱️ The time it takes for a projectile to stop at its highest point is equal to the time it takes to return to the launch point.
- 🔢 The initial velocity upward is the same magnitude as the final velocity when the projectile returns to its original height.
- 🎯 The greatest range for a projectile is achieved when launched at a 45-degree angle, while the maximum height is achieved at a 75-degree angle.
- ⚖️ Complementary angles, such as 30 and 60 degrees, result in the same range because they sum up to 90 degrees.
- 📈 As the angle of launch increases, the vertical displacement of the projectile also increases.
- 📉 At the highest point of its trajectory, the vertical component of the projectile's velocity is zero, and the time to reach this point is half of the total time of flight.
- 📚 An example problem is solved in the lesson, calculating the maximum height and horizontal displacement (range) of a baseball hit at an angle of 25 degrees with a velocity of 30 m/s.
Q & A
What is the basic concept of projectile motion?
-Projectile motion is the motion of an object thrown at an angle to the horizontal. It involves a parabolic trajectory with constant horizontal velocity and vertical motion with constant acceleration due to gravity.
What are the two components of projectile motion?
-The two components of projectile motion are the horizontal component, where the acceleration is zero and the velocity is constant, and the vertical component, where the acceleration is constant and equal to the acceleration due to gravity (9.8 m/s^2).
What is the relationship between the angle of release and the range of a projectile?
-The angle of release affects the range of a projectile. The maximum range is achieved when the projectile is launched at an angle of 45 degrees with respect to the horizontal.
What is the relationship between the angle of release and the maximum height of a projectile?
-The maximum height of a projectile is achieved when it is launched at an angle of 75 degrees. As the angle of launch increases, the vertical displacement of the projectile also increases.
What is the significance of complementary angles in projectile motion?
-Complementary angles, such as 30 and 60 degrees, are significant in projectile motion because they result in the same range. This is because the sum of the angles is 90 degrees, and the projectile's path is symmetrical around the vertical axis.
How is the vertical velocity of a projectile affected by gravity during its flight?
-The vertical velocity of a projectile decreases as it rises due to the opposing force of gravity. At the highest point, the vertical velocity is zero as the projectile momentarily stops before descending. As it falls back to the ground, the vertical velocity increases because the direction of motion aligns with the gravitational force.
What is the formula used to calculate the maximum height reached by a projectile?
-The formula to calculate the maximum height (dy) reached by a projectile is given by: dy = (vi * sin(theta))^2 / (2 * g), where vi is the initial velocity, theta is the angle of launch, and g is the acceleration due to gravity.
How do you calculate the horizontal displacement or range of a projectile?
-The horizontal displacement (dx) or range of a projectile is calculated using the formula: dx = vi * cos(theta) * t, where vi is the initial velocity, theta is the angle of launch, and t is the total time of flight.
What is the total time of flight for a projectile launched at an angle?
-The total time of flight for a projectile is calculated using the formula: t = (2 * vi * sin(theta)) / g, where vi is the initial velocity, theta is the angle of launch, and g is the acceleration due to gravity.
What is the significance of the initial velocity in projectile motion?
-The initial velocity is significant as it determines the magnitude of both the horizontal and vertical components of the projectile's motion. It affects the range, maximum height, and the overall trajectory of the projectile.
How does the time taken to reach the maximum height relate to the total time of flight for a projectile?
-The time taken to reach the maximum height is half of the total time of flight. This is because the projectile takes an equal amount of time to ascend to its highest point and to descend back to the point of launch.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Projectile Motion Part II | Quarter 4 Grade 9 Science Week 2 Lesson

S9Q4W2 | Part 2: PROJECTILE MOTION

FISIKA KELAS X || CONTOH SOAL GERAK PARABOLA TIPE 1 (Parabola Penuh)
Gerak Parabola • Part 3: Contoh Soal Gerak Parabola Dimulai dari Ketinggian Tertentu
kinematics 6of6 projectile motion final
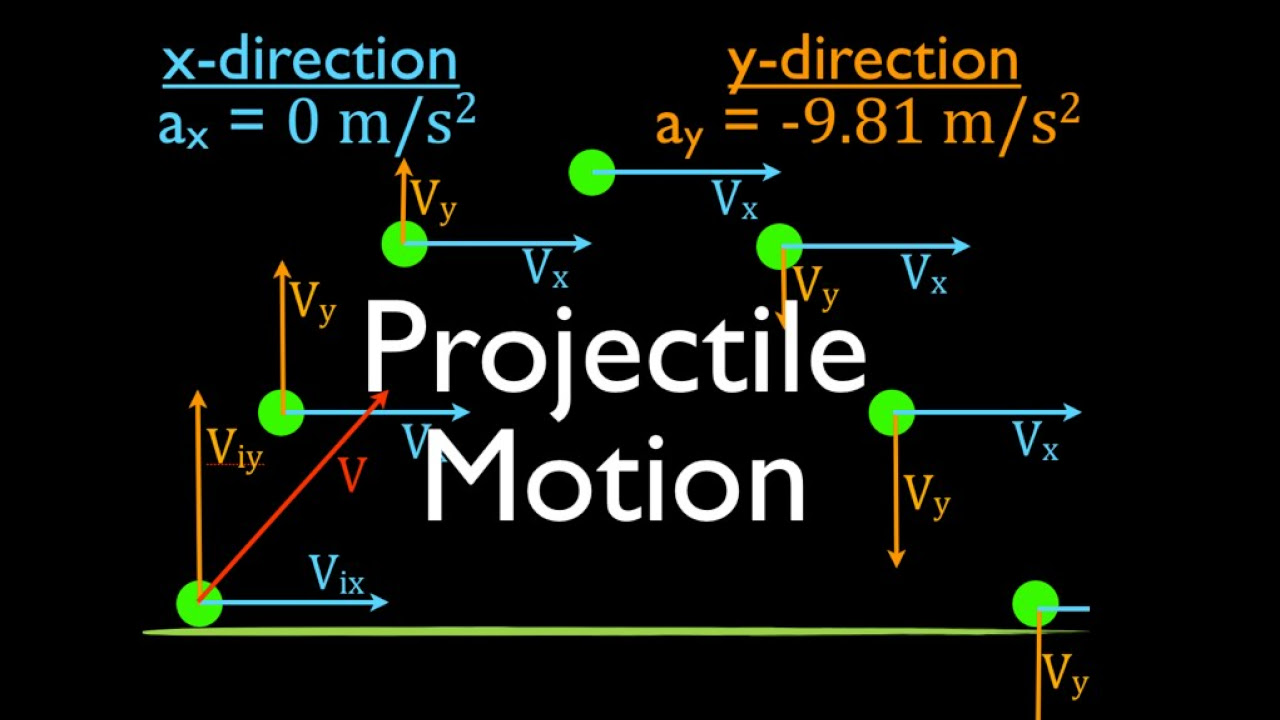
Two Dimensional Motion (1 of 4) An Explanation
5.0 / 5 (0 votes)
