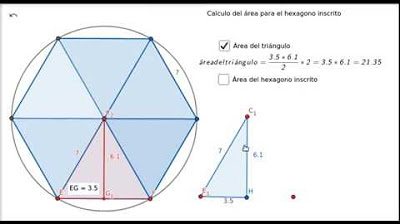
Área de polígono inscrito en circunferencia- formula general
Summary
TLDREn este video se explica cómo derivar una fórmula general para calcular el área de un polígono inscrito en un círculo. Usando conceptos de geometría y trigonometría, se demuestra cómo el área depende del radio del círculo y del número de lados del polígono. A través de la división del círculo, el cálculo del ángulo central y el uso de identidades trigonométricas, se llega a la fórmula final, que permite calcular el área solo conociendo el radio y el número de lados del polígono. Esta fórmula es útil para diversos tipos de polígonos regulares inscritos.
Takeaways
- 😀 El objetivo del vídeo es encontrar una fórmula general para calcular el área de un polígono inscrito en un círculo.
- 😀 Se requiere conocer solo dos datos: el radio del círculo (r) y el número de lados del polígono (n).
- 😀 Para dibujar un polígono dentro de un círculo, se debe dividir la circunferencia entre el número de lados del polígono.
- 😀 El ángulo central de cada lado del polígono se calcula dividiendo 360° entre el número de lados (α).
- 😀 Al dividir el ángulo central (α) a la mitad, obtenemos el ángulo θ, el cual es crucial para derivar el área del polígono.
- 😀 Usando trigonometría, el seno de θ se relaciona con los catetos de los triángulos rectángulos formados por el apotema y el radio del círculo.
- 😀 La longitud de un lado del polígono (l) se puede expresar como 2r × seno(π/n).
- 😀 El perímetro del polígono se obtiene multiplicando la longitud de un lado (l) por el número de lados (n).
- 😀 La fórmula estándar para el área de un polígono es A = (P × a) / 2, donde P es el perímetro y a es el apotema.
- 😀 Después de sustituir las expresiones para el perímetro y el apotema, la fórmula general para el área es A = (n × r² × seno(2π/n)) / 2.
- 😀 La fórmula derivada solo requiere el valor del radio (r) y el número de lados (n) para calcular el área de cualquier polígono regular inscrito en un círculo.
Q & A
¿Cómo se determina el ángulo alfa en el caso de un polígono inscrito en un círculo?
-El ángulo alfa se obtiene dividiendo la circunferencia del círculo (360° o 2π radianes) entre el número de lados del polígono (n), es decir, α = 360° / n o α = 2π / n.
¿Qué se obtiene al trazar una bisectriz del ángulo alfa?
-Al trazar la bisectriz del ángulo alfa, se obtiene un ángulo de mitad, denominado θ, que es igual a α / 2, es decir, θ = π / n.
¿Cuál es la fórmula que relaciona el seno del ángulo θ con el cateto opuesto y la hipotenusa en los triángulos rectángulos formados?
-La fórmula es sin(θ) = cateto opuesto / hipotenusa, donde el cateto opuesto es la mitad de un lado del polígono (l / 2) y la hipotenusa es el radio del círculo (r).
¿Cómo se calcula la longitud de un lado (l) del polígono?
-La longitud del lado (l) se calcula usando la fórmula l = 2r * sin(π / n), donde r es el radio del círculo y n es el número de lados del polígono.
¿Cómo se obtiene el perímetro del polígono inscrito?
-El perímetro se obtiene multiplicando la longitud de un lado (l) por el número de lados (n), es decir, P = n * l. Como l = 2r * sin(π / n), el perímetro es P = n * 2r * sin(π / n).
¿Qué es el apotema de un polígono inscrito en un círculo?
-El apotema es la distancia desde el centro del círculo hasta el centro de uno de los lados del polígono. Se calcula usando la fórmula apotema = r * cos(π / n), donde r es el radio del círculo.
¿Cómo se calcula el área de un polígono inscrito en un círculo?
-El área se calcula con la fórmula A = (P * apotema) / 2, donde P es el perímetro y el apotema es la distancia desde el centro hasta el centro de un lado.
¿Qué se obtiene al sustituir el perímetro y el apotema en la fórmula del área?
-Sustituyendo el perímetro (n * 2r * sin(π / n)) y el apotema (r * cos(π / n)) en la fórmula A = (P * apotema) / 2, se obtiene A = n * r² * sin(π / n) * cos(π / n).
¿Cómo se simplifica la expresión para el área utilizando una identidad trigonométrica?
-Usando la identidad trigonométrica 2 * sin(θ) * cos(θ) = sin(2θ), la fórmula se simplifica a A = (n * r² / 2) * sin(2π / n).
¿Cuál es la fórmula final para el área de un polígono inscrito en un círculo?
-La fórmula final para el área de un polígono inscrito en un círculo es A = (n * r² / 2) * sin(2π / n), donde n es el número de lados y r es el radio del círculo.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)