ÁREA DE UN POLIGONO EN EL PLANO CARTESIANO
Summary
TLDREn este video, la profesora Ingrid enseña cómo calcular el área de figuras en el plano cartesiano utilizando vértices dados. Explica un método paso a paso para encontrar el área de un polígono aplicando una fórmula específica, ejemplificada con un triángulo. Ingrid realiza operaciones de multiplicación y suma de coordenadas, tomando el valor absoluto al final para encontrar el área correcta. El resultado final es de 20.5 unidades cuadradas. Además, invita a los espectadores a suscribirse al canal y dejar sus dudas o sugerencias en los comentarios para futuros ejercicios.
Takeaways
- 📐 La profesora Ingrid enseña cómo calcular el área de figuras en el plano cartesiano.
- 🔺 Los vértices de un polígono son dados para formar la figura cuyo área se necesita calcular.
- 📝 Se utiliza una fórmula que involucra las coordenadas de los vértices para obtener el área.
- 🔄 El primer vértice debe repetirse al final de la fórmula.
- ✏️ El área se calcula mediante un medio del valor absoluto de las multiplicaciones entre las coordenadas.
- 📊 Las diagonales hacia abajo se multiplican y los resultados se suman o restan según sus signos.
- 🔄 Las diagonales hacia arriba también se multiplican, pero sus signos cambian según las reglas de signos.
- 🔢 Las operaciones algebraicas siguen la lógica de suma y resta de números con signos diferentes.
- 🟢 El valor absoluto se aplica al resultado final de las operaciones para obtener un área positiva.
- ✅ El resultado final del ejercicio es un área de 20.5 unidades cuadradas.
Q & A
¿Cuál es el tema principal que se aborda en el video?
-El tema principal del video es cómo calcular el área de figuras en el plano cartesiano usando la fórmula para polígonos dados sus vértices.
¿Qué fórmula se utiliza para calcular el área de un polígono en el plano cartesiano?
-Se utiliza la fórmula de un medio del valor absoluto de la suma de los productos de las coordenadas de los vértices, recorriendo todos los puntos del polígono y cerrando el ciclo con el primer punto.
¿Cómo se estructuran los vértices en la fórmula presentada en el video?
-Los vértices se estructuran en pares ordenados (x1, y1), (x2, y2), …, (xn, yn), y al final se repite el primer vértice (x1, y1) para cerrar la fórmula.
¿Qué operaciones se realizan para calcular el área con la fórmula?
-Primero se multiplican las coordenadas siguiendo diagonales hacia abajo y se suman los resultados. Luego, se multiplican las coordenadas siguiendo diagonales hacia arriba y se suman esos resultados. Finalmente, se restan las sumas obtenidas y se divide entre 2 para obtener el área.
¿Por qué se toma el valor absoluto en la fórmula del área?
-Se toma el valor absoluto para asegurarse de que el área sea siempre positiva, ya que puede ser que al realizar las operaciones algunas sumas den resultados negativos.
En el ejemplo del video, ¿cuáles son los vértices del triángulo utilizado?
-Los vértices del triángulo utilizado en el ejemplo son (-4, -3), (-1, 5) y (3, 2).
¿Cuál fue el resultado del área del triángulo en el ejemplo del video?
-El área del triángulo resultante fue 20.5 unidades cuadradas.
¿Qué hay que hacer al final de la fórmula para obtener el área correcta del polígono?
-Se debe dividir el resultado del valor absoluto entre 2 para obtener el área correcta del polígono.
¿Qué recomendación hace la profesora sobre cómo colocar los vértices en la fórmula?
-La profesora recomienda que, al utilizar la fórmula, se debe cerrar el ciclo volviendo a escribir el primer vértice al final para que la fórmula se aplique correctamente.
¿Qué se debe tener en cuenta al hacer las operaciones con las coordenadas en la fórmula?
-Se debe tener en cuenta el orden de las operaciones y los signos de las multiplicaciones, ya que estos influirán en el resultado final.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
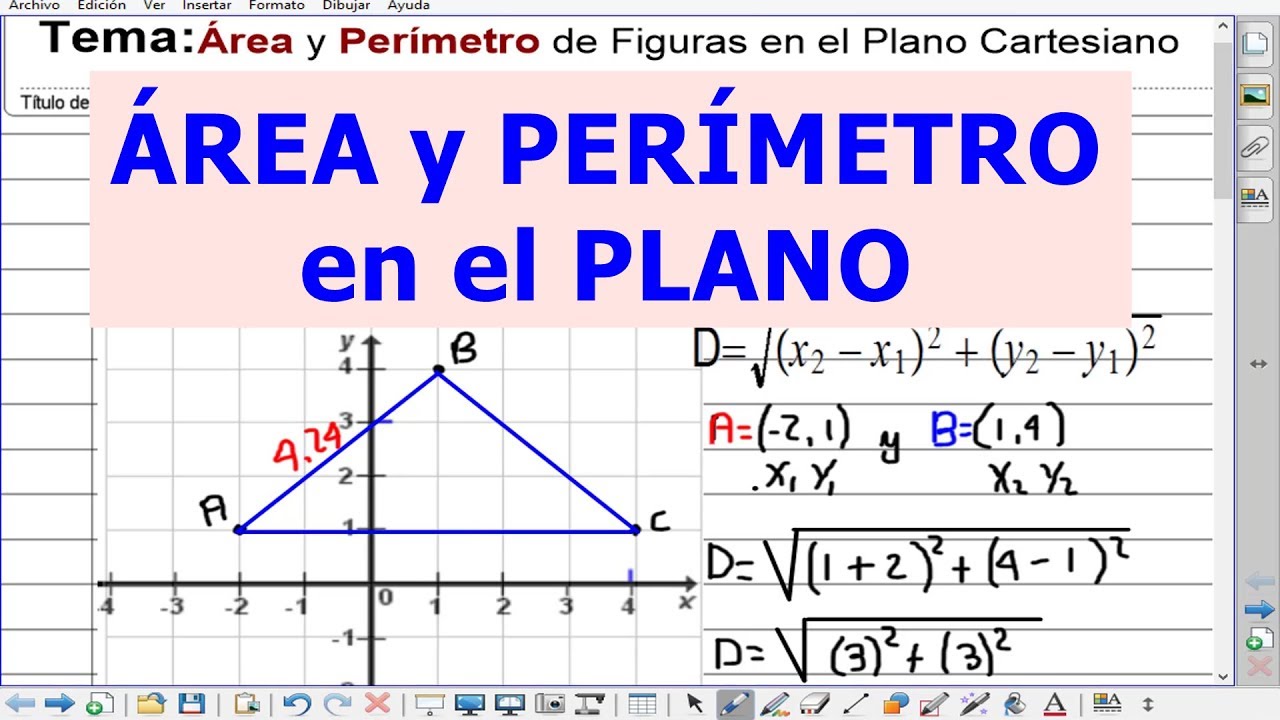
Área y Perímetro de Figuras en el Plano Cartesiano.
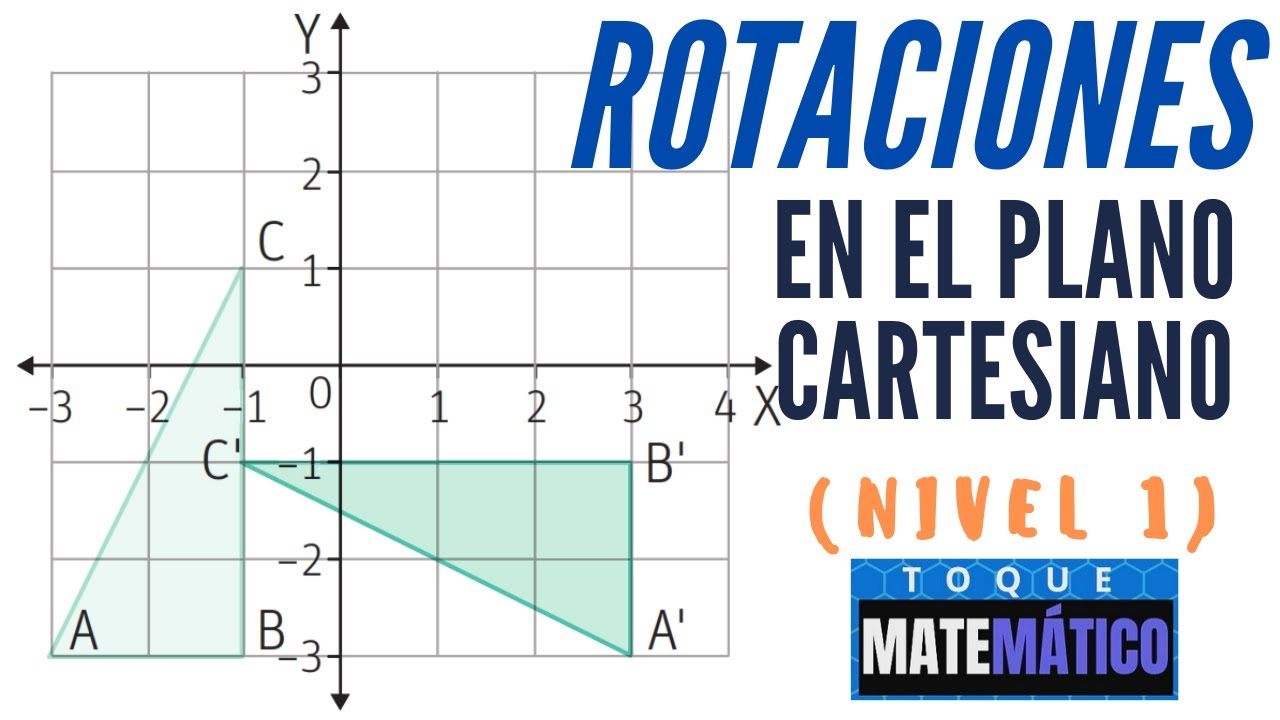
Rotaciones en el Plano Cartesiano ✔ 👌 [TRANSFORMACIONES ISOMETRICAS: ROTACIÓN]

Área de un paralelogramo con Vectores

DISTANCIA ENTRE DOS PUNTOS

LEVANTAMIENTO DE UN TERRENO POR COORDENADAS

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos
5.0 / 5 (0 votes)
