Method of Undetermined Coefficients 1
Summary
TLDRThis video introduces the method of undetermined coefficients for solving non-homogeneous linear differential equations. It begins by solving the homogeneous equation, then focuses on finding a particular solution based on the form of G(x). The first example, with G(x) as a constant, leads to a simple constant particular solution. In the second example, G(x) is a polynomial, requiring a more complex particular solution. The video explains how to match G(x) with an appropriate polynomial form for Yp, laying the groundwork for more advanced cases.
Takeaways
- 🧮 The method of undetermined coefficients is used to solve non-homogeneous linear differential equations with constant coefficients.
- 🔗 The first step is to solve the homogeneous version of the differential equation by finding its characteristic equation.
- ✍️ In the given example, solving the characteristic equation led to the homogeneous solution: y_h = C1 * e^(2x) + C2 * e^(-x).
- 📊 To find the particular solution, guess a form of the solution based on the form of the G(x) term.
- 🛠️ For constant G(x) (like 8 in the example), assume the particular solution is also a constant, then plug it into the differential equation to find its value.
- 🔄 The general solution is the sum of the homogeneous and particular solutions: y = C1 * e^(2x) + C2 * e^(-x) - 4.
- 🔧 For polynomial G(x) terms, the particular solution must also be a polynomial of matching degree, such as ax² + bx + c for G(x) = 4x².
- 📐 The undetermined coefficients (a, b, c, etc.) are found by plugging the guessed solution into the equation and matching terms with G(x).
- 📈 A key step is ensuring that the homogeneous and particular solutions do not overlap; otherwise, the form of the particular solution must be modified.
- 🔄 The same process applies to other types of G(x), such as exponential or trigonometric terms, covered in future examples.
Q & A
What is the method of undetermined coefficients?
-The method of undetermined coefficients is a technique used to find the particular solution of a non-homogeneous linear differential equation. The idea is to guess the form of the particular solution based on the structure of the non-homogeneous term (G(x)) and solve for unknown constants.
When can the method of undetermined coefficients be used?
-This method can be used when dealing with a linear differential equation with constant coefficients, and the non-homogeneous term G(x) is of a form that can be matched by a specific guess (e.g., polynomials, exponentials, or trigonometric functions).
What are the general steps in solving a differential equation using the method of undetermined coefficients?
-The steps include: 1) Solving the homogeneous version of the equation to get the homogeneous solution, 2) Guessing the form of the particular solution based on G(x), 3) Substituting the guessed form into the differential equation, and 4) Solving for the undetermined coefficients to find the particular solution.
How is the homogeneous solution found in the example y'' - y' - 2y = 8?
-The homogeneous solution is found by solving the characteristic equation derived from the homogeneous differential equation y'' - y' - 2y = 0, which gives roots r = 2 and r = -1. The general homogeneous solution is then y_h = C1 * e^(2x) + C2 * e^(-x).
What is the guessed form of the particular solution when G(x) is a constant?
-When G(x) is a constant (like 8 in the example), the guessed form of the particular solution is also a constant. In the given example, y_p = A, and solving for A gives y_p = -4.
Why do we sometimes need to modify the guessed form of the particular solution?
-The guessed form of the particular solution needs to be modified if it overlaps with the homogeneous solution. If the guessed form is already part of the homogeneous solution, it must be multiplied by x (or higher powers of x) to ensure the solutions do not overlap.
How is the particular solution guessed when G(x) is a polynomial like 4x^2?
-When G(x) is a polynomial, such as 4x^2, the guessed form for the particular solution must be a polynomial of the same degree. For 4x^2, the guessed form is y_p = Ax^2 + Bx + C, where A, B, and C are undetermined coefficients.
How are the undetermined coefficients found in the example with G(x) = 4x^2?
-The undetermined coefficients are found by substituting the guessed form y_p = Ax^2 + Bx + C into the differential equation, simplifying both sides, and equating the coefficients of like terms (x^2, x, constants). This system of equations is then solved to find A, B, and C.
What is the final general solution for the differential equation y'' - y' - 2y = 4x^2?
-The final general solution is the sum of the homogeneous and particular solutions. For the example y'' - y' - 2y = 4x^2, the solution is y = C1 * e^(2x) + C2 * e^(-x) - 2x^2 + 2x - 3.
How do you determine the form of the particular solution based on G(x)?
-The form of the particular solution depends on G(x). For a constant G(x), the guess is a constant. For G(x) as a polynomial of degree n, the guess is a polynomial of degree n. If G(x) involves exponentials or trigonometric functions, the guess is of a similar form with undetermined coefficients.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Finalizando a semana 3
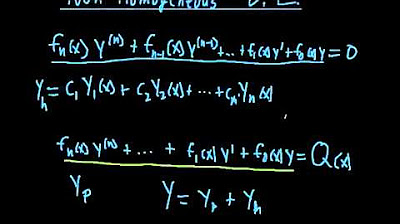
General Solution to Non-Homogeneous DE

A concept of Differential Equation

Introducing Weird Differential Equations: Delay, Fractional, Integro, Stochastic!

Recurrence Relation | Solution of Recurrence Relation | Discrete Mathematics by Gp sir

🔵03 - Linear and Non-Linear Differential Equations: Solved Examples
5.0 / 5 (0 votes)
