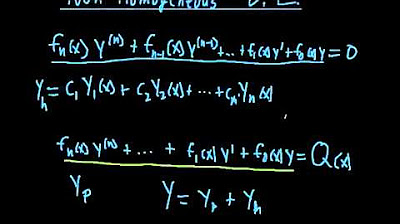Ecuaciones diferenciales Homogéneas | Ejemplo 5

Summary

This educational video script offers a detailed walkthrough of solving a homogeneous second-order differential equation. The instructor begins by recommending viewers watch introductory videos for context. The script then guides through the process of identifying the equation as homogeneous, separating variables, and transforming it into a solvable form. It covers the method of substitution, simplification, and integration, ultimately leading to the solution with a constant of integration. The instructor emphasizes the importance of practice and invites viewers to engage with more content for a deeper understanding of differential equations.

Takeaways

• 📚 The video is a tutorial on solving homogeneous differential equations, specifically for viewers who are new to the topic.
• 🔍 The script emphasizes checking if an equation is homogeneous and of the first degree before attempting to solve it.
• 📝 The first step in solving the equation is to separate the differentials, which involves moving terms involving 'dx' to one side and 'dy' to the other.
• 🔄 The process includes a substitution technique to transform the homogeneous equation into a separable variables equation.
• ✍️ The script provides a detailed walkthrough of the algebraic manipulations needed to simplify the equation, such as factoring and combining like terms.
• 📉 The video demonstrates the integration process, including handling of inverse trigonometric integrals and logarithmic integrals.
• 🔍 It highlights the importance of recognizing when an integral can be solved by substitution or parts, and when it requires a different method.
• 📐 The tutorial includes a step to eliminate fractions by multiplying through by the denominator, simplifying the equation.
• 📝 The final step involves back-substitution to convert the solution back into the original variables, x and y.
• 📚 The presenter suggests practicing with the given example and comparing it with the solution provided in the video for better understanding.
• 👍 The video concludes with an encouragement for viewers to subscribe, comment, share, and like the video for further assistance and support.

Q & A

What is the main topic of the video?

The main topic of the video is solving homogeneous differential equations.

What does the instructor recommend for viewers who are new to the topic?

The instructor recommends that new viewers watch the introductory video on homogeneous differential equations before proceeding with this one.

How does the instructor verify if the given equation is homogeneous?

The instructor verifies if the equation is homogeneous by checking if both terms in the equation have the same degree and if the functions in the numerator and denominator are homogeneous of the same degree.

What is the first step in solving a homogeneous differential equation according to the script?

The first step is to separate the differentials, which involves moving the differential of x to the other side of the equation and multiplying the terms accordingly.

What substitution does the instructor suggest to transform the homogeneous equation into a separable variables equation?

The instructor suggests substituting the variable 'y' with 'u' (or any letter with a hat, like 'u^'), and replacing the differential 'dy' with the differential of the new variable.

How does the instructor approach the process of integrating after separating the variables?

The instructor integrates by first simplifying the equation, then identifying direct integrations and inverse trigonometric integrals, and applying the appropriate integration techniques.

What is the significance of the instructor's observation about the terms having the same variable?

The observation about terms having the same variable is significant for factorization, which simplifies the equation and makes it easier to integrate.

How does the instructor handle the presence of fractions in the integrated equation?

The instructor eliminates fractions by multiplying the entire equation by the denominator, which simplifies the equation and removes the need for fractions.

What technique does the instructor use to simplify the final answer involving logarithms and arctangents?

The instructor uses the property of logarithms that allows combining multiple logarithms into a single logarithm with the arguments multiplied together.

Why does the instructor suggest reviewing the final answer for any remaining substituted variables?

The instructor suggests reviewing the final answer to ensure that all substituted variables have been correctly replaced back to their original form, ensuring the solution is in terms of the original variables.

What does the instructor recommend for viewers who want to practice solving homogeneous differential equations?

The instructor recommends that viewers practice by watching the next video, pausing it to attempt the exercise, and then comparing their work with the instructor's explanation.

Outlines

00:00

📚 Introduction to Solving Homogeneous Differential Equations

The speaker begins by greeting the audience and introducing the topic of solving homogeneous differential equations. They suggest that newcomers watch the introductory video before proceeding. The speaker then presents a differential equation and explains the first step in solving it, which is to check if the equation is homogeneous and of the first degree. They clarify that both terms in the equation should have the same degree for it to be considered homogeneous. The process of separating the differentials is outlined, which involves moving terms to the other side of the equation and multiplying by necessary factors to isolate the functions and their differentials.

05:01

🔍 Detailed Steps in Transforming the Equation

This paragraph delves into the specifics of transforming the given homogeneous differential equation into a form that allows for separation of variables. The speaker describes the process of replacing the variable 'y' with a new variable 'u' to simplify the equation. They provide a step-by-step guide on how to perform the substitution, including taking the derivative of 'u' with respect to 'x' and replacing 'y' and its differential 'dy' with expressions involving 'u'. The goal is to rewrite the equation in a way that makes it easier to integrate by separating the variables.

10:02

📝 Separating Variables and Integrating

The speaker continues by demonstrating how to separate the variables in the transformed equation and prepare it for integration. They explain the process of moving all terms involving 'dx' to one side and all terms involving 'du' to the other side. After successfully separating the variables, the speaker discusses the integration of each part. They mention that one part of the equation can be integrated directly, while the other part may require a substitution method, which they will explain in a separate video.

15:03

🧐 Simplifying the Integrated Equation

In this part, the speaker focuses on simplifying the integrated equation. They discuss the possibility of simplifying the equation by canceling out terms and using properties of logarithms and inverse trigonometric functions. The speaker also mentions changing the variable back to its original form and eliminating fractions by multiplying through by the common denominator. They emphasize the importance of simplifying the solution to make it as clear and concise as possible.

20:04

🎓 Conclusion and Encouragement to Practice

The speaker concludes by summarizing the steps taken to solve the homogeneous differential equation and encourages the audience to practice the process. They suggest watching the complete course for a deeper understanding of the topic or other recommended videos for further study. The speaker also hopes that the information was useful, especially for those preparing for assignments or exams, and ends the video with an invitation to subscribe, comment, share, and like the video.

Keywords

💡Differential Equations

Differential equations are mathematical equations that involve a function and its derivatives. In the context of the video, the theme revolves around solving a specific type of differential equation known as a homogeneous differential equation. The script mentions the process of solving these equations, emphasizing the steps and methods involved in finding solutions.

💡Homogeneous Differential Equation

A homogeneous differential equation is a special type of differential equation where the equation can be written in a form that is homogeneous, meaning that each term is proportional to a single function and its derivatives. The video script describes how to identify and solve such equations, using the properties of homogeneity to simplify the process.

💡Separation of Variables

Separation of variables is a method used to solve differential equations by rearranging the equation so that all terms involving one variable are on one side and the terms involving the other variable are on the opposite side. The script illustrates this technique by moving terms involving 'x' to one side and those involving 'y' to the other, facilitating the integration of each side separately.

💡Derivative

The derivative of a function represents the rate at which the function changes with respect to its variable. In the script, the derivative is initially cleared, meaning it is isolated on one side of the equation, which is a common first step in solving differential equations.

💡Integral

An integral is the reverse process of differentiation, used to find the function when its derivative is known. The video script discusses the process of integrating both sides of the separated equation to find the original function 'y' in terms of 'x'.

💡Substitution

Substitution is a technique used in calculus to simplify complex expressions or equations by replacing a part of the expression with a new variable. The script describes a specific substitution where 'y' is replaced with 'u' to transform the homogeneous differential equation into a form that is easier to integrate.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are used in various mathematical contexts, including solving differential equations. The script mentions inverse trigonometric functions, such as arctangent, which appear as part of the solution to the integrated equation.

💡Logarithmic Functions

Logarithmic functions are the inverse of exponential functions and are used in solving equations where the variable is the exponent. The script includes the natural logarithm function in the final solution of the differential equation, illustrating its use in integrating certain types of functions.

💡Integration by Parts

Integration by parts is a specific method for integrating products of functions, which is based on the product rule for differentiation. Although not explicitly used in the script, the mention of direct integration and substitution implies that integration by parts could be a relevant technique for certain integrals.

💡Constant of Integration

The constant of integration is added to the solution of an indefinite integral to account for the fact that the derivative of a constant is zero. The script concludes with the addition of this constant to the final solution of the differential equation, emphasizing its importance in the completeness of the solution.

Highlights

Introduction to the course on differential equations, focusing on solving homogeneous differential equations.

Recommendation for newcomers to watch introductory videos on recognizing and solving homogeneous differential equations.

Explanation of the first step in solving a differential equation: ensuring the derivative is isolated.

Verification of the equation's homogeneity and degree, emphasizing the importance of terms having the same degree.

The method of separating differentials to transform the equation into a form that allows for separation of variables.

The choice of substitution to simplify the equation, opting for the function with more positive terms for ease of calculation.

Derivation of the substitution method, including the replacement of variables and differentials to create a separable equation.

Multiplication of terms and the reorganization of the equation to facilitate the separation of variables.

Observation of terms to identify which can be factored out or eliminated to simplify the equation further.

The process of integrating the separated variables, including the identification of integral types and methods.

Simplification of the equation by canceling out terms and using properties of logarithms and trigonometric functions.

The use of substitution to solve integrals, particularly when dealing with inverse trigonometric functions.

Identification of integrals that can be solved directly or through methods such as parts or substitution.

Reversion to original variables after integration, ensuring the solution is in terms of the initial problem's variables.

Final simplification of the solution, combining logarithmic terms and using properties of exponents to achieve a simplified form.

Advice on checking the final solution for any remaining substituted variables and ensuring the solution is in terms of the original variables only.

Encouragement for students to practice with the provided exercises and to compare their work with the explained solutions.

Invitation for students to subscribe, comment, share, and like the video for further engagement and support.

Transcripts

qué tal amigos espero que estén muy bien

bienvenidos al curso de ecuaciones

diferenciales y ahora veremos un ejemplo

de solución de una ecuación diferencial

homogénea

sí

[Música]

y en este vídeo vamos a resolver esta

ecuación diferencial que pues obviamente

es homogénea pero antes de empezar les

recomiendo si ustedes este es el primer

vídeo que ven de solución de ecuaciones

diferenciales homogéneas les recomiendo

que vayan por lo menos al primer vídeo

en el que hago una introducción a este

tema porque allí les explico

detenidamente cómo saber qué es una

ecuación diferencial homogénea como

reconocer si una ecuación es diferencial

a ojén ya o no y cuáles son los pasos a

seguir para resolverlo sí pero si

ustedes ya vieron esos vídeos pues

pueden tomar este ejercicio como una

práctica entonces pausa en el vídeo

resuelvan el ejercicio y comparan con lo

que yo voy a hacer yo voy a empezar

obviamente un poco más rápido porque

pues ya hemos visto varios vídeos no

primero que todo cuál es el primer paso

despejar la derivada en este caso la

derivada ya está despejada entonces pues

no hago ese paso sí pues porque ya es

como lo más fácil digámoslo así ya

cuando está despejada verificamos si

esta ecuación si es homogénea si en este

caso arriba hay dos términos cada uno

este término no tiene exponente o sea

exponente uno éste tampoco tiene

exponente o sea export

como los dos términos este es de grado 1

y este es de grado 1

entonces la ecuación de arriba es

homogénea de grado 1 lo mismo sucede

abajo el primer término es de grado 1 el

segundo término también es de grado 1

como los dos términos son del mismo

grado o sea de grado 1 entonces ésta

también es homogénea de grado 1 y como

las dos la de arriba la función de

arriba y la de abajo del denominador son

homogéneas del mismo grado entonces esta

es una ecuación diferencial homogénea

entonces ya sabemos que para resolverla

pues vamos a seguir los pasos de las

homogéneas el primer paso cuál es

separar los diferenciales el diferencial

de x que generalmente está abajo lo

pasamos al otro lado a multiplicar y

esto que está en el denominador la

pasamos para el otro lado para separar

las funciones con sus diferenciales no

entonces esto que está dividiendo pasa a

multiplicar como son dos términos que

eran entre paréntesis ye más x

acompañado de el diferencial de y igual

y este diferencial de x pasa acá

entonces aquí se lleve menos x como son

dos términos los colocamos entre

paréntesis porque van a ir acompañados

de el diferencial

y aquí observamos cuál es la letra que

vamos a reemplazar porque hay aquí

acordemos que vamos a hacer un reemplazo

para cambiar esta ecuación que es

homogénea por una que es de variables

separables bueno entonces observamos las

dos funciones la que está acompañando al

diferencial de x y la que está

acompañando al diferencial de ye perdón

y al diferencial de x en este caso son

muy parecidas entonces cuál es la más

fácil recomendación yo generalmente como

cojo como más fácil la que tenga más

positivos generalmente cuando hay

negativos pues no resulta complicándose

un poquito más bueno entonces consejo

como la función más fácil está

acompañando al diferencial de y lo que

vamos a reemplazar es la letra g

entonces por aquí escribo que

reemplazamos la letra g por un excel

siempre después generalmente por u equis

o cualquier letra con la equis como

vamos a reemplazar la aie también

tenemos que reemplazar el diferencial de

y entonces derivamos la derivada de y es

el diferencial de igual como esto es una

multiplicación primero por derivada del

segundo primero por derivada del segundo

más segundo por derivada

del primero entonces vamos a reemplazar

de esta forma como nos quedaría siempre

donde diga la letra y lo reemplazamos

por equis y donde diga el diferencial de

hielo reemplazamos por toda esta suma

entonces reemplazamos las equis quedan

iguales solamente reemplazamos las y

aquí abrimos paréntesis ya la ye la

reemplazamos por equis más x y eso está

acompañado del diferencial de y que

tenemos que cambiarlo entonces borro

aquí porque estamos cambiando la y aquí

en lugar del diferencial de allí escribo

esto o deje el perdón de x mas x de eeuu

como son dos términos siempre van entre

paréntesis

aquí dice x acompañado del diferencial

de ye igual aquí nuevamente empieza con

la letra g que la ye la cambiamos por

equis menos equis acompañado del

diferencial de x que no se cambia no

aquí al final debemos revisar que aquí

ya no debe aparecer en ningún lado la

letra i porque es la que estamos

reemplazando ahora sí ya como hicimos el

reemplazo entonces esta es una ecuación

de variables separables entonces tenemos

que separarlas para eso pues primero

generalmente nos va a quedar

multiplicaciones entonces hacemos esas

multiplicaciones acordémonos que aquí

como son dos términos y los términos que

hacemos multiplicamos el primer término

por los otros dos que están en el otro

paréntesis y lo mismo haríamos aquí

entonces pues voy a hoy explicándoles lo

mismo aquí la multiplicación que tenemos

que hacer es el diferencial de x lo

multiplicamos por estos dos términos que

están dentro del paréntesis entonces

como nos queda aquí nos quedaría x x de

equis entonces uno por uno es o al

cuadrado

x no hay más entonces queda x acompañado

de el diferencial de x seguimos con la

uv pero ahora la multiplicamos por x de

entonces y no hay más entonces más por

más da más y x x x x al cuadrado con el

diferencial de eeuu lo mismo hacemos

ahora con la letra x entonces

multiplicamos esa letra por los dos

términos que están en el otro paréntesis

entonces primero la x con de x entonces

generalmente sea primero la u

x de x aunque si ustedes escriben x y

está igualmente bien porque la

multiplicación no importa el orden no es

conmutativa y nuevamente la x con x de

entonces x por x mas x más da más x x x

es x al cuadrado acompañados del

diferencial de aquí igual y

multiplicamos estos dos x por de x pues

es x de x menos x x de x que pues es x

de x ya como están todos los términos

separados entonces ahora sí observamos

para separar los diferenciales no todos

los términos con el diferencial de x a

un lado

y con el diferencial de eeuu al otro

lado aquí observó que en este lado están

dos términos con el diferencial de x

entonces ya voy a pasar todos los del

diferencial de x para la derecha y los

del diferencial de eeuu los voy a dejar

acá o sea este término que tiene el

diferencial de x lo pasó para el otro

lado este término que también tiene el

diferencial de x también lo pasó para el

otro lado y aquí van a quedar los que

tiene a la izquierda los que tienen el

diferencial de eeuu entonces estos dos

términos quedan iguales o x al cuadrado

de eeuu

y x al cuadrado dv

quedan con su mismo signo igual a estos

dos que están al lado derecho

y estos dos que pasan para el otro lado

entonces este está positivo cambia de

signo no sea estaba sumando pasa a

restar menos o al cuadrado x de equis

y este o x de x como estaba positivo

menos x de x aquí que es lo que tenemos

que hacer factorizar los diferenciales

pero antes aquí estoy observando lo

siguiente bien que aquí dice un x de x -

x de x entonces como son iguales y uno

positivo y el otro negativo generalmente

uno menos 1 a 0 no generalmente uno dice

se eliminan porque esto da cero así como

para que me quede más fácil ahora si

aquí a la izquierda que es lo que se

factorizar siempre se va a factorizar el

diferencial de eeuu y muchas veces se

pueden factorizar algo más en este caso

miren que los dos términos tienen la x

al cuadrado entonces voy a factorizar x

al cuadrado de entonces pues lo escribió

primero no x al cuadrado por el

diferencial del factor de aquí si a este

término le quitamos estos dos nos queda

solamente la u más y aquí si quitamos

todo pues nos queda el número uno x al

cuadrado

/ / x al cuadrado de úbeda

1 aquí nos quedaría igual aquí que lo

que vamos a factorizar pues el

diferencial no entonces sería el

diferencial de x pero además en los dos

términos está la letra x entonces factor

hizo los dos entonces a bueno otra cosa

miren que otros consejos que les voy

dando no miren que los dos términos

están negativos entonces para no para

que no queden tantos términos negativos

voy a factorizar ese negativo también

porque se repiten entonces factor hizo

el negativo y factor hizo la equis con

el diferencial de x eso factor de

entonces aquí si quitamos el negativo

quitamos la xy quitamos el diferencial

de x quitamos todo o sea queda uno o

esto dividido entre eso mismo down aquí

menos x menos dan más o al cuadrado

bueno si le quitamos a todo este término

el negativo la equis y el de x nos queda

solamente o al cuadrado positivo

acuérdense que cuando factor izamos el

negativo lo que está aquí adentro queda

con signos cambiado no eso hay que

revisarlo el primero estaba negativo que

da positivo y el segundo estaba negativo

que a positivo no que esta era la idea

que estos términos llame

en positivos y ahora sí ya después de

haber factor izado ya podemos entonces

separar las variables que estará la idea

no entonces a la izquierda está el

diferencial de o sea todo lo que tiene

la uv a la izquierda a la derecha está

el diferencial de x todo lo que tenga la

equis a la derecha entonces aquí a la

izquierda este x al cuadrado lo tengo

que quitar entonces solamente me queda

el diferencial generalmente se deja al

final no entonces nos quedaría uno más

uno acompañado del diferencial de eeuu

está x al cuadrado va a pasar a dividir

aquí lo que tenga la 1 tenemos que pasar

para el otro lado de la igualdad no aquí

es igual aquí bueno algo que yo estoy

observando desde que factor hice es que

aquí dice uno más o al cuadrado esto

generalmente acuérdense que a veces

cuando están en el denominador resulta

siendo una integral trigonométricas

inversa bueno ahorita miramos a ver si

sí pero eso generalmente yo lo hago de

una vez bueno como para reír revisar

entonces aquí nos quedaría dividido

entre uno más o al cuadrado eso que pasa

a dividir pues pasa al denominador

perdón uno más o al cuadrado aquí no hay

necesidad del paréntesis porque como

esto no se está operando con nada no hay

problema ahora a la derecha está menos x

de x y está x al cuadrado que estaba

multiplicando pasa al otro lado a

dividir entonces aquí queda sobre x al

cuadrado y como ya separamos las

variables ahora sí podemos integrar

entonces cositas que observo acá primero

aquí podemos simplificar una x de arriba

con una de abajo otra cosita que veo

pues aquí ya lo primero que miro es si

se puede resolver por sustitución en

este caso si yo derivó esto no me da lo

de arriba acordémonos que para poderlo

resolverla por sustitución si la

derivada de abajo da lo de arriba o algo

muy parecido entonces es porque sí se

puede por sustitución en este caso la

derivada de esto la derivada de uno es

cero y la derivada de al cuadrado es dos

y tv pero aquí dice 2

dv pero acompañado de ese 1 como está

dentro de un paréntesis no se puede por

sustitución bueno por partes pues

tampoco se puede porque

partes generalmente son multiplicaciones

pero lo que sí veo es que puedo separar

la un aparte y el uno aparte no porque

se puede separar porque recordemos que

tenemos por ejemplo fracciones

homogéneas supongamos cinco tercios más

ocho tercios si acordémonos que la suma

de fracciones homogéneas o sea del mismo

denominador se puede hacer de la

siguiente forma sigue quedando el mismo

denominador y lo de arriba los sumamos y

ya aquí sería 5 813 creo pues aquí voy a

colocar las sumas y 5 más 8 entonces que

es lo que vamos a hacer vamos a realizar

el paso inverso sean bien que tenemos

una suma con algo abajo eso lo podemos

cambiar por una suma si en la que hay

dos fracciones sí o sea separando los

dos de arriba y el denominador queda

para los dos entonces cómo nos quedaría

primero van a quedar dos integrales no

entonces primero la integral de

solamente lado

con el diferencial de eeuu sí porque

estamos separando él a su mano sobre y

lo que está en el denominador va a

quedar para las dos fracciones o sea uno

más o al cuadrado

luego seguiría más integral del 1

entonces el 1 por dv pues de una vez lo

quito es solamente de un sobre y el

denominador lo colocamos también igual

no uno más o al cuadrado aquí si ya

observó que esta es una derivada directa

sí que es trigonométricas inversa porque

es de u sobre estas uno generalmente se

las tiene que aprender de memoria no y

aquí arriba también observó que no es

trigonométricas inversa pero que ya se

puede por parte de perdón por

sustitución porque al derivar aquí nos

da un teu sí que es lo de arriba bueno

pero bueno ya lo voy a explicar aquí

como les decía simplificamos una equis

entonces como arriba y abajo está la

equis esa equis de arriba se va con una

de las dos de abajo y abajo queda una

sola

además el negativo generalmente uno lo

saca para atrás de la integral entonces

menos la integral de arriba quedó

solamente de x sobre y abajo quedó la x

entonces esta integral es directa no

esta integral se resuelve por

sustitución como les decía en los vídeos

anteriores generalmente cuando se

resuelva una integral por sustitución o

por partes

realicen la aparte y aquí colocan

solamente el resultado para que no se

les alargue el proceso yo generalmente

cuando estoy haciendo esto en un

cuaderno lo que hago es cojo por ejemplo

esta integral que es la que se resuelve

por sustitución la hago a un ladito del

cuaderno le hago un redondeo como para

identificar que era eso y escribo aquí

solamente en la respuesta y reemplazamos

lo del denominador entonces que es es

uno más o al cuadrado eso lo cambiamos

por una letra en este caso otra letra

que no haya estado en el ejercicio la

letra v derivamos la derivada de uno es

cero la derivada de igual cuadrado es

bajarle el exponente bajamos el

exponente le restamos uno como derivamos

la acompañamos de la diferencial de y

estos son av igual la derivada de v es

el diferencial de v aquí que es lo que

tenemos que buscar arriba tenemos que

buscar

dv sí que ya casi está bueno esto es una

uva ya arreglarla porque nos confundimos

aquí ya dice vudú pero ese 2 me sobra

que es lo que tengo que hacer pues

pasarlo para el otro lado entonces me

queda

igual al diferencial de v y el 2

estaba multiplicando pasas a dividir

ahora si realizamos ese reemplazo cuál

es donde veamos un 1 más o al cuadrado

lo cambiamos por la letra v y donde

veamos

lo cambiamos por dv sobre 2 entonces

aquí nos queda igual ya obviamente va a

saltar paso 1 v

dv eso es de b sobre 2 y abajo en el

denominador dice uno más o al cuadrado

que eso es v vuelvo a decirles aquí me

salte varios pasos no igual la integral

bueno este 2 sale de la integral como

está en el denominado sale en el

denominador arriba pues colocaríamos un

1 y nos queda la integral de debe sobre

b o de tve sobre v que es logaritmo

natural de v pero la v la cambiamos

nuevamente por uno más o al cuadrado

entonces esta es la respuesta de la

primera integral como les decía esto

aparte y de una vez aquí colocamos el

resultado está integral el resultado es

un medio del logaritmo natural de uno

más o al cuadrado

esta integral que bueno esta ya es una

trigonométricas inversa que bueno esa

integral les voy a dejar el link en la

descripción del vídeo de el vídeo en el

que les explico las integrales

trigonométricas inversas que son muy

sencillas solamente hay que aprender nos

lastimamos lo así entonces la

integral de esto es bueno aquí dice más

arco tangente es la integral de esta es

la arco tangente que se puede colocar

como arco tangente o tangente a la menos

1 arco tangente de eeuu igual aquí dice

menos y la integral del de x sobre x es

logaritmo natural de x y pues obviamente

como ya integramos entonces le agregamos

la constante de integración y ya como

integramos entonces recordemos que la

ecuación diferencial al comienzo estaba

solamente con la letra x la variable x y

la variable y entonces recuerden que

tenemos que volver a esas variables

entonces la letra la tenemos que volver

a cambiar nuevamente por la letra x y la

letra i y para eso pues tenemos que

acordarnos de la sustitución que hicimos

al comienzo no la sustitución que

hicimos fue la ye la cambiamos por y x

como aquí vamos a cambiarla entonces

despejamos de aquí la pasando esta x que

está multiplicando a dividir entonces

nos queda dividido entre x igual av

o sea que ahora donde esté la letra la

voy a cambiar por ye sobre x pero además

aquí veo otro paso que se puede hacer

miren que aquí hay un término que es

este otro término que es este otro

término el logaritmo natural y otro

término la c si ustedes observan aquí

hay un solo término que tiene una

fracción entonces para quitar esa

fracción que ya no me quede en

fracciones porque pues es como más

complicado con fracciones entonces voy a

multiplicar toda la ecuación por este

denominador sí para que para eliminarlo

y eso como nos queda por ejemplo el

primer término

si lo multiplicamos por 2 que lo podemos

multiplicar aquí a la derecha eso es lo

de menos porque no importa el orden aquí

se puede simplificar o eliminar el 2 del

denominador con el 2 por el que estoy

multiplicando la ecuación entonces pasa

lo que les decía se elimina la fracción

y entonces colocamos lo que nos quedó no

entonces el primer término al

multiplicarlo por 2 nos quedó 1 por el

logaritmo natural que eso es el

logaritmo natural de uno más o al

cuadrado pero acordemos que la ula vamos

a reemplazar por 10 sobre x como esaú

aquí donde la vamos a reemplazar está

elevada al cuadrado entonces acordémonos

que aquí tenemos que elevar cada uno de

los dos al cuadrado entonces quedaría

llega al cuadrado sobre x al cuadrado

luego sigue más y acordemos que estamos

multiplicando todos los términos por 2

no para poder eliminar este entonces

este segundo término por 2 pues que

quedaría dos veces la arco tangente de

la letra a perdón la ula estamos

cambiando entonces no copiamos la uv

sino que copiamos 10 sobre x

igual a menos logaritmo natural como

aquí ya no está el agua entonces todos

los términos los multiplicamos por 2

entonces menos logaritmo natural de x

por 2 es menos dos veces el logaritmo

natural de x más la cee por 2 pues es

dos veces la letra c y ahora sí esta es

la respuesta de nuestra ecuación

diferencial porque pues porque ya

integramos y porque ya le volvimos a las

variables iniciales pero en matemáticas

pues generalmente se trata de entregar

una respuesta simplifica entonces vamos

a tratar de simplificar para esto por lo

que vamos a hacer es lo que hemos hecho

en vídeos anteriores miren que aquí hay

un término con logaritmo natural y otro

terminó con logaritmo natural entonces

lo que voy a hacer es pasarlos para el

mismo lado de la igualdad para

convertirlos en un solo logaritmo

natural y pues bueno voy a mirar a ver

qué más se puede hacer por ahora además

acordémonos que cuando multiplicamos dos

por una constante eso es otra constante

entonces en lugar de esto voy a escribir

constante 1 como para decir que esto es

otra constante entonces pasamos los

logaritmos para la izquierda porque aquí

hay un logaritmo éste lo puedo pasar

para que me quede positivo entonces me

queda este logaritmo quedaría

logaritmo natural pero pues de una vez

voy a hacer esta operación uno más al

cuadrado sobre x al cuadrado

aquí le colocamos un 1 en el denominador

y nos queda el método de la carita feliz

1 x x al cuadrado que es x al cuadrado

luego cruzado 1 x x al cuadrado que es x

al cuadrado más y al cuadrado por 1 que

eso es y al cuadrado entonces esta

operación me queda como x al cuadrado

más y al cuadrado sobre x al cuadrado

ahora este logaritmo que lo voy a pasar

para el otro lado como está negativo si

está restando pasa al otro lado a sumar

entonces quedaría más dos veces el

logaritmo natural de x igual y al otro

lado pues va a quedar la arco tangente y

éste se 1 constante 1 no generalmente

primero se escribe siempre se explique

se escribe al final la constante

entonces voy a pasarla a calcular con

tangente para acá como está sumando pasa

a restar entonces menos 2 arco tangente

de 10 sobre x este logaritmo ya lo

escribí allá y más la constante 1 para

que coloque los logaritmos en el mismo

lado para poderlos unir pero acuérdense

que para poder unir los logaritmos no

deben estar multiplicados por nada

aquí vamos a utilizar la propiedad que

dice que cuando hay algo multiplicando

el logaritmo ese numerito lo podemos

pasar aquí como exponente del argumento

entonces para no hacer un paso con eso

simplemente lo borro de aquí y lo

escribo aquí como exponente del

argumentos y ahora sí están los dos

logaritmos acordémonos que si tenemos la

suma de dos logaritmos eso se puede

escribir como un solo logaritmo y sus

argumentos quedan multiplicados y

entonces aquí nos quedaría un solo

logaritmo el logaritmo natural y estos

dos argumentos quedan multiplicados

entonces el primer argumento x al

cuadrado más y al cuadrado sobre x al

cuadrado más perdón más no g acordémonos

que esos argumentos quedan multiplicados

entonces por este otro argumento por

primero argumento por el segundo que es

x al cuadrado y al otro lado pues no veo

algo así que se puede hacer entonces voy

a dejarlo igual 2 negativos perdón menos

2 arco tangente de ye sobre x más la

constante número uno aquí miren que y

muchas veces va a pasar eso como lo

hemos visto en vídeos anteriores

aquí se puede eliminar esta equis al

cuadrado con esta x al cuadrado porque

se pueden eliminar porque ésta está

dividiendo a todo y ésta está

multiplicando a todos y entonces podemos

eliminarlas o simplificar las pilas

porque este x al cuadrado acuérdense que

no se puede simplificar porque no está

multiplicando esta es sumando a todos

los demás entonces por eso ésta no se

podía eliminar ni aquí desde aquí aquí

no se puede eliminar se se puede

eliminar está porque está multiplicando

y bueno la verdad no veo así nada más

que se pueda realizar si vuelvo a

decirles eso depende del gusto de cada

quien si uno quiere por ejemplo puede

pasar este arco tangente para la

izquierda para que quede sola la

constante aquí no se puede despejar la

aie porque miren la que está aquí dentro

del logaritmo natural y dentro del arco

tangente entonces no se puede despejar

entonces yo lo voy a dejar así

simplemente voy a copiar lo que quedó el

logaritmo natural de x al cuadrado más

ya al cuadrado igual a menos 2 veces el

arco tangente más la constante número

uno acuérdense que al final yo les

recomiendo revisar que no esté la letra

1

debe estar al final la letra x nada más

y la letra o sea como constante sí

porque a veces uno a uno se le olvide a

cambiar alguna u y entonces aquí ya veo

que no hay ninguna y entonces hasta aquí

termino como siempre pues no en este

caso no les voy a dejar vídeos como los

vídeos de las homogéneas porque como se

dan cuenta es un proceso muy largo que

no cabría aquí en el tablero para

explicarles entonces pues si quieren

practicar los invito a que vayan al

siguiente vídeo y practiquen con ese

ejercicio pueden pausar el vídeo y

después revisan y comparan con lo que yo

les voy a explicar bueno amigos espero

que les haya gustado la clase si les

gustó los invito a que vean el curso

completo para que profundicen un poco

más sobre este tema o algunos vídeos

recomendados y si están aquí por alguna

tarea o evaluación espero que les vaya

muy bien los invito a que se suscriban

comenten compartan y le den laical vídeo

y no siendo más bye bye

[Música]