Algebra - Proportional and Nonproportional Relationships
Summary
TLDRThis video concludes a chapter on equations of lines by exploring proportional and non-proportional relationships in linear equations. The instructor explains that proportional relationships pass through the origin and follow the form y = kx, where k is a constant. Non-proportional relationships, however, include an additional constant, which alters the proportion. Through examples, tables, and graphing, the differences between these relationships are illustrated. The video also revisits arithmetic sequences, highlighting how to determine whether a sequence is proportional or not, rounding off the chapter with a review of key concepts.
Takeaways
- 📏 Proportional relationships occur when an equation passes through the origin (0, 0) and is of the form y = kx.
- ✏️ Direct variations are examples of proportional relationships, where k is the constant of variation.
- 🔄 You can set up a proportion between any two values in a proportional relationship, and the ratios will be equal.
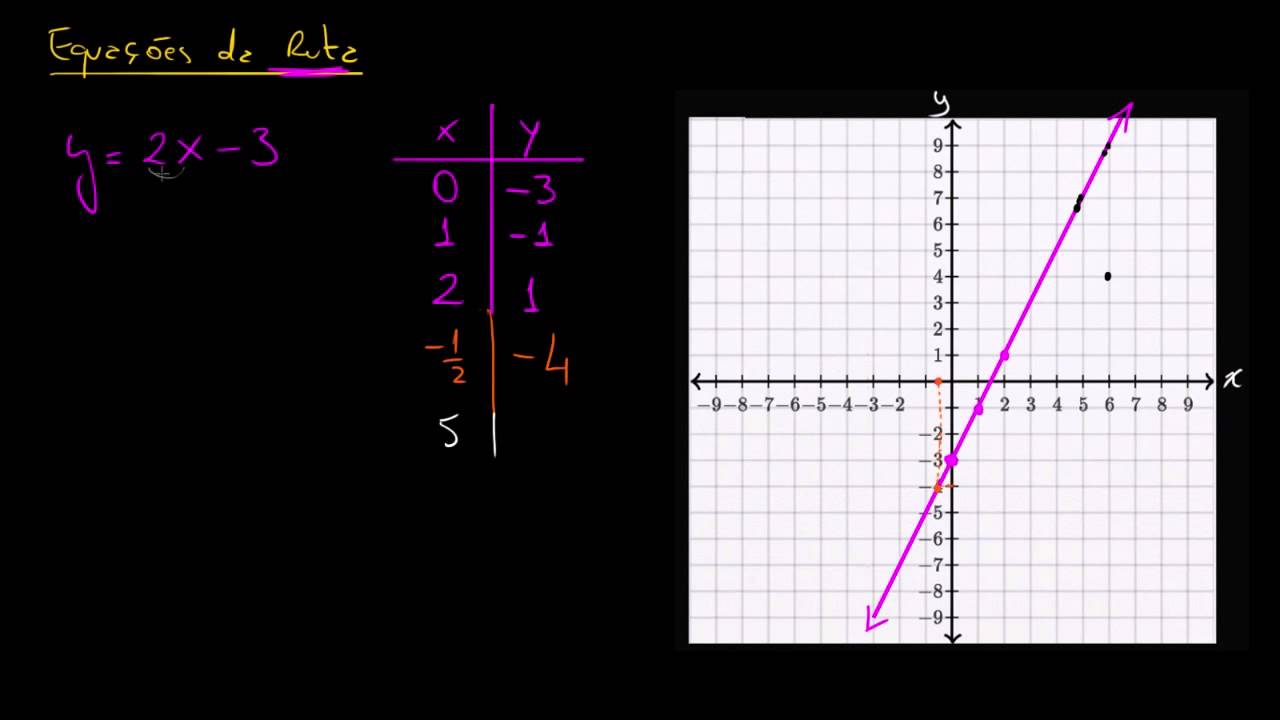
- ⚖️ Non-proportional relationships occur when there is an additional constant (e.g., y = 2x - 1), which prevents the equation from passing through the origin.
- 📉 A non-proportional relationship alters the balance of the equation, making proportions between values unequal.
- 📝 To determine the equation of a proportional relationship, use the slope formula (change in y / change in x) and apply it to the equation y = kx.
- 🧮 Non-proportional relationships follow the format y = mx + b, where b is the y-intercept and affects the overall equation.
- 📊 Proportional relationships will always pass through the origin (0, 0) when graphed, while non-proportional relationships intersect at the y-intercept.
- 🔢 Arithmetic sequences can also be analyzed to determine whether they follow proportional or non-proportional patterns.
- ✍️ When analyzing arithmetic sequences, if there is a constant difference but an additional number at the end of the equation, it signals a non-proportional relationship.
Q & A
What is a proportional relationship in the context of linear equations?
-A proportional relationship in the context of linear equations is when the equation passes through the origin (0,0) and is of the form y = kx, where k is the constant of variation. This means the ratio of y to x is constant.
How can you determine if a linear equation represents a proportional relationship?
-You can determine if a linear equation represents a proportional relationship by checking if it passes through the origin (0,0) and if it can be written in the form y = kx without any additional constants.
What is an example of a proportional relationship?
-An example of a proportional relationship is the equation y = 3x. This equation passes through the origin and maintains a constant ratio between y and x.
What defines a non-proportional relationship in linear equations?
-A non-proportional relationship in linear equations is defined by the presence of an additional constant term, making the equation of the form y = kx + b, where b is not zero. This means the line does not pass through the origin.
How does the equation y = 2x - 1 illustrate a non-proportional relationship?
-The equation y = 2x - 1 illustrates a non-proportional relationship because it includes the additional constant term -1, which prevents the line from passing through the origin and alters the constant ratio between y and x.
What happens to the graph of a non-proportional relationship?
-The graph of a non-proportional relationship will not pass through the origin. Instead, it will intersect the y-axis at the y-intercept value, which is determined by the constant term in the equation.
How can you identify the y-intercept in a linear equation?
-You can identify the y-intercept in a linear equation by looking at the constant term in the equation of the form y = kx + b. The y-intercept is the value of b, which is the point where the line crosses the y-axis.
Why is y = 5x considered a proportional relationship?
-The equation y = 5x is considered a proportional relationship because it passes through the origin and maintains a constant ratio of y to x with no additional constant term.
How does the table of values help determine if a relationship is proportional?
-The table of values helps determine if a relationship is proportional by allowing you to see if the ratio between y and x is constant for all pairs of values. If the ratio is consistent and the line passes through the origin, the relationship is proportional.
What is the difference between direct variation and proportional relationships?
-There is no difference between direct variation and proportional relationships in the context of linear equations. Both terms describe a linear relationship that passes through the origin and is of the form y = kx.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Teorema de TALES | Prof. Gis/
Equações lineares com duas variáveis e seus gráficos

ILLUSTRATING SYSTEMS OF LINEAR EQUATIONS IN TWO VARIABLES || GRADE 8 MATHEMATICS Q1

Illustrating Linear Equations in Two Vairables | Writing Linear Equations in Standard Form

Aljabar Linier Pertemuan 2_Sistem Persamaan Linier part 1/4

🔵03 - Linear and Non-Linear Differential Equations: Solved Examples
5.0 / 5 (0 votes)
