ILLUSTRATING SYSTEMS OF LINEAR EQUATIONS IN TWO VARIABLES || GRADE 8 MATHEMATICS Q1
Summary
TLDRThis video explains systems of linear equations in two variables, covering key concepts such as linear equations, systems of equations, and their graphical representations. The script outlines how to write and solve systems of linear equations, discusses the three types of solutions—intersecting lines, coinciding lines, and parallel lines—and categorizes systems as consistent, inconsistent, dependent, or independent. It also demonstrates how to identify solutions based on the slope and y-intercept of the equations. Through examples, the video helps viewers understand how to interpret these systems visually and algebraically for solving real-world problems.
Takeaways
- 😀 A linear equation in two variables can be written in the form 'a x + b y = c', where a, b, and c are real numbers, and a and b cannot be zero.
- 😀 A system of linear equations involves two or more linear equations considered together.
- 😀 A solution to a system of linear equations in two variables is an ordered pair that satisfies both equations in the system.
- 😀 The graph of a system of linear equations can result in three types of graphs: intersecting lines, coinciding lines, and parallel lines.
- 😀 Intersecting lines represent a system that has exactly one solution, and it is called consistent and independent.
- 😀 Coinciding lines (same lines) represent a system that has infinitely many solutions, and it is called consistent and dependent.
- 😀 Parallel lines represent a system that has no solution, and it is called inconsistent.
- 😀 The standard form of a system of linear equations can be written as two equations, e.g., 'a₁x + b₁y = c₁' and 'a₂x + b₂y = c₂'.
- 😀 Systems of linear equations can be analyzed by inspecting the slopes and y-intercepts to determine the type of system (intersecting, coinciding, or parallel).
- 😀 A system of linear equations with unequal slopes and different y-intercepts represents intersecting lines, which means the system is consistent and independent.
- 😀 If the slopes are equal but the y-intercepts differ, the lines are parallel, and the system is inconsistent with no solution.
Q & A
What is a linear equation in two variables?
-A linear equation in two variables is an equation that can be written in the form Ax + By = C, where A, B, and C are real numbers, and A and B are not equal to zero.
What is a system of linear equations?
-A system of linear equations consists of two or more linear equations considered together.
What is the general form of a system of linear equations in two variables?
-The general form of a system of linear equations in two variables is: A1x + B1y = C1 and A2x + B2y = C2.
What does it mean for a system of linear equations to have a solution?
-A solution to a system of linear equations in two variables consists of an ordered pair that satisfies both equations.
What are the three types of graphs that can represent systems of linear equations in two variables?
-The three types of graphs are: intersecting lines, coinciding lines, and parallel lines.
What does it mean if the lines representing a system of linear equations intersect at exactly one point?
-If the lines intersect at exactly one point, the system is consistent and independent, meaning there is exactly one solution.
What happens if the lines representing a system of linear equations are coincident?
-If the lines are coincident, meaning they lie on top of each other, the system is consistent and dependent, and it has infinitely many solutions.
What does it mean if the lines representing a system of linear equations are parallel?
-If the lines are parallel, the system is inconsistent, meaning there is no solution.
How can you determine if two lines are intersecting, coinciding, or parallel without graphing them?
-You can determine the relationship between the lines by comparing their slopes and y-intercepts. If the slopes are different, the lines are intersecting. If the slopes are the same but the y-intercepts are different, the lines are parallel. If both the slopes and y-intercepts are the same, the lines are coinciding.
How can you determine if a system of linear equations has one solution, infinitely many solutions, or no solution?
-By analyzing the slopes and y-intercepts of the equations: If the slopes are different, the system has one solution. If the slopes and y-intercepts are the same, the system has infinitely many solutions. If the slopes are the same but the y-intercepts differ, the system has no solution.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Aljabar Linier Pertemuan 2_Sistem Persamaan Linier part 1/4
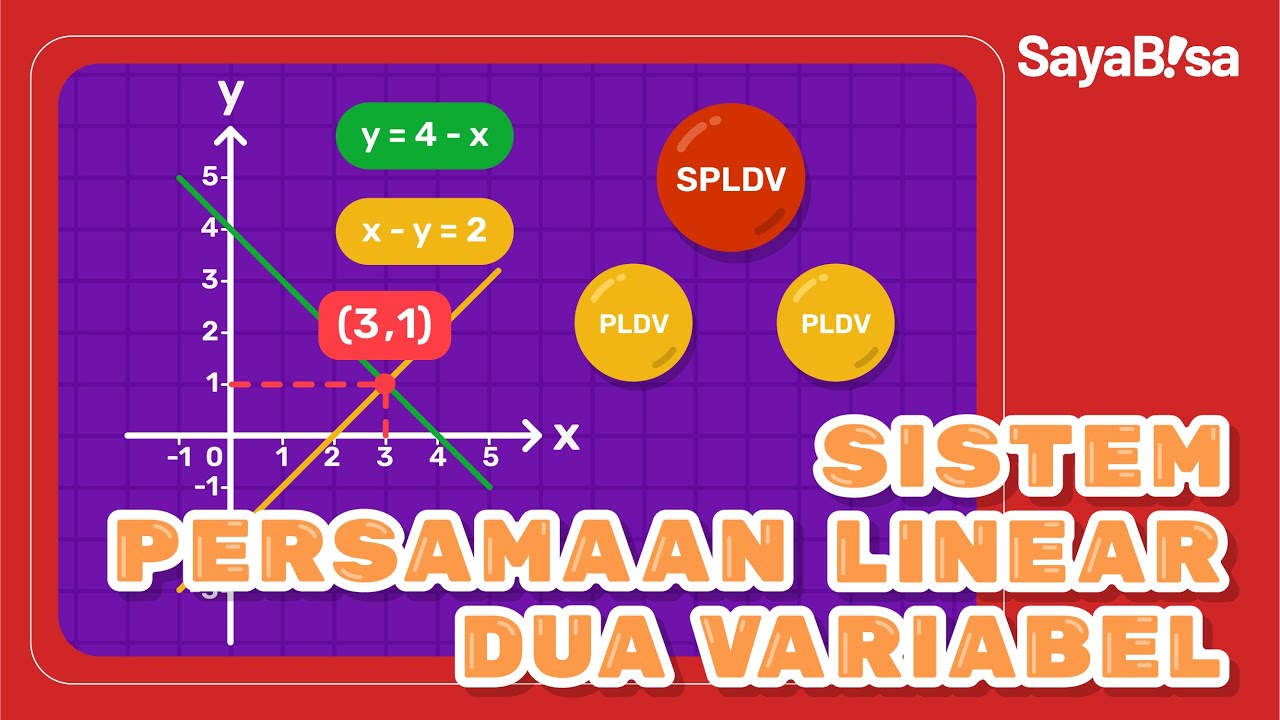
Sistem Persamaan Linear Dua Variabel | Matematika | SayaBisa

Sistem persamaan linear dua variabel kelas 10 - metode grafik

PERSAMAAN LINEAR DUA VARIABEL (PLDV) KELAS 9

SPLDV [Part 1] - Mengenal SPLDV + Metode Grafik

Pembahasan Buku PR Matematika Kelas XB Intan Pariwara|Asesmen 2 Pilihan Ganda No.1-10|Kurmer
5.0 / 5 (0 votes)