Understanding Stress Transformation and Mohr's Circle
Summary
TLDRThis video introduces the concept of stress transformation and Mohr's circle, essential tools for understanding stress states in materials. It explains how rotating a 2D stress element can change the normal and shear stresses, and how these can be calculated using transformation equations. The principal stresses, which represent the maximum and minimum normal stresses, are highlighted, with Mohr's circle offering a graphical method for visualization. The video also touches on 3D stress elements and the use of multiple Mohr's circles to analyze complex stress states, crucial for predicting material failure.
Takeaways
- 😀 Stress transformation involves rotating a stress element to determine how normal and shear stresses change with orientation.
- 😀 The stress element represents the stresses acting at a specific point within a body, and it is used to visualize these stresses in 2D for plane stress conditions.
- 😀 In a simple example with axial load, the stress element will only have a normal stress of Sigma-X, while shear stresses will be zero.
- 😀 Rotating the stress element can provide different values for normal and shear stresses depending on the chosen angle (Theta).
- 😀 Stress transformation equations are used to calculate normal and shear stresses at different orientations of the stress element.
- 😀 Principal stresses occur when the shear stress is zero, corresponding to maximum and minimum normal stresses on certain planes.
- 😀 Principal stresses are crucial for predicting failure, as they represent the highest and lowest normal stresses at a location.
- 😀 Mohr's circle is a graphical method for determining normal and shear stresses at various orientations without using transformation equations.
- 😀 Mohr's circle is constructed by plotting the stress conditions at different faces of the stress element and drawing a circle that represents the stress state.
- 😀 The radius of Mohr's circle represents the maximum shear stress, and the points where the circle intersects the horizontal axis indicate the principal stresses.
- 😀 Angles in Mohr's circle are doubled compared to the angle of rotation of the stress element. This difference is important when calculating principal stress angles.
Q & A
What is the purpose of a stress element in stress transformation?
-A stress element is a useful way of visualizing and describing the stresses acting at a single point within a body. It helps to understand how normal and shear stresses are distributed across different faces of the element.
What is meant by a 2D stress element in this context?
-A 2D stress element refers to a two-dimensional representation of stress at a point, where normal and shear stresses are considered on the four faces of the element. This applies to a state of plane stress.
How does rotating the stress element affect the stress components?
-When the stress element is rotated, the normal and shear stress components change. By rotating the stress element, you can determine the stress state at different orientations using the stress transformation equations.
What are the principal stresses, and why are they important?
-Principal stresses are the maximum and minimum normal stresses acting on a stress element. They are important for predicting failure because they represent the extreme stress conditions where shear stresses are zero.
What is the relationship between the principal stresses and shear stresses?
-When the normal stresses are at their maximum or minimum (principal stresses), the shear stresses are zero. The faces on which these shear stresses are zero are known as principal planes.
How does Mohr's circle help in stress transformation analysis?
-Mohr's circle is a graphical tool that simplifies the process of determining normal and shear stresses at different orientations of the stress element, without the need for complex equations.
What do the axes of Mohr's circle represent?
-In Mohr's circle, the horizontal axis represents normal stress, while the vertical axis represents shear stress. This allows the stresses at different orientations to be visualized as points on the circle.
How are principal stresses identified on Mohr's circle?
-The principal stresses are located where Mohr's circle intersects the horizontal axis, as shear stress is zero at these points. The maximum and minimum normal stresses correspond to these points.
What is the significance of the radius of Mohr's circle?
-The radius of Mohr's circle represents the maximum shear stress. It can be determined either by measuring the distance on the circle or by using the circle's radius formula.
Why do angles in Mohr's circle differ from the actual rotation angle of the stress element?
-Angles in Mohr's circle are doubled compared to the rotation angle of the stress element. This is because Mohr's circle plots shear stress as a function of both normal stress components, resulting in an angle that is twice the actual rotation angle of the stress element.
How does stress transformation extend from 2D to 3D?
-In 3D, stress elements involve three principal stresses, and Mohr’s circle is extended to three dimensions, involving three different circles. This helps to visualize all combinations of normal and shear stresses for a 3D stress state.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Transformasi Tegangan (Part 1) - Mekanika Material / Kekuatan Material

Understanding Torsion
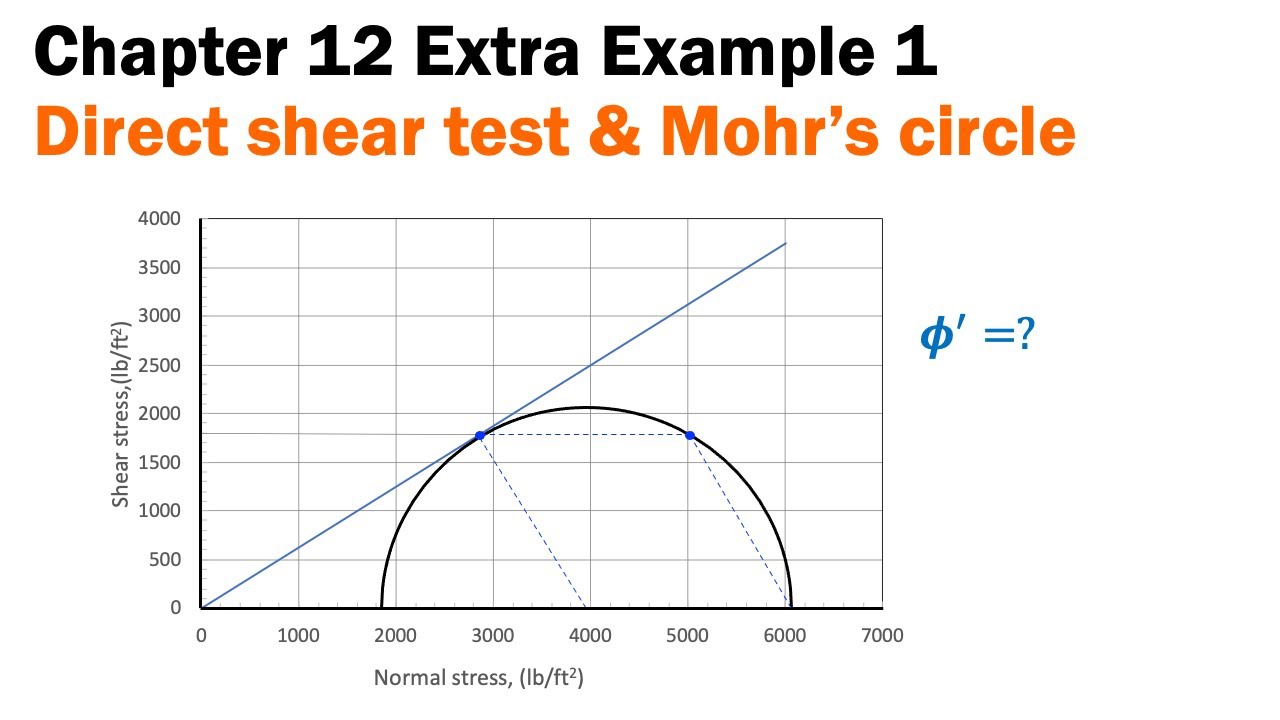
Chapter 12 Extra Example 1 - Direct shear test and Mohr's circle at failure

Understanding plasticity theory (for Mises UMAT)

Aprenda agora o que é tensão na resistência dos materiais (ResMat)
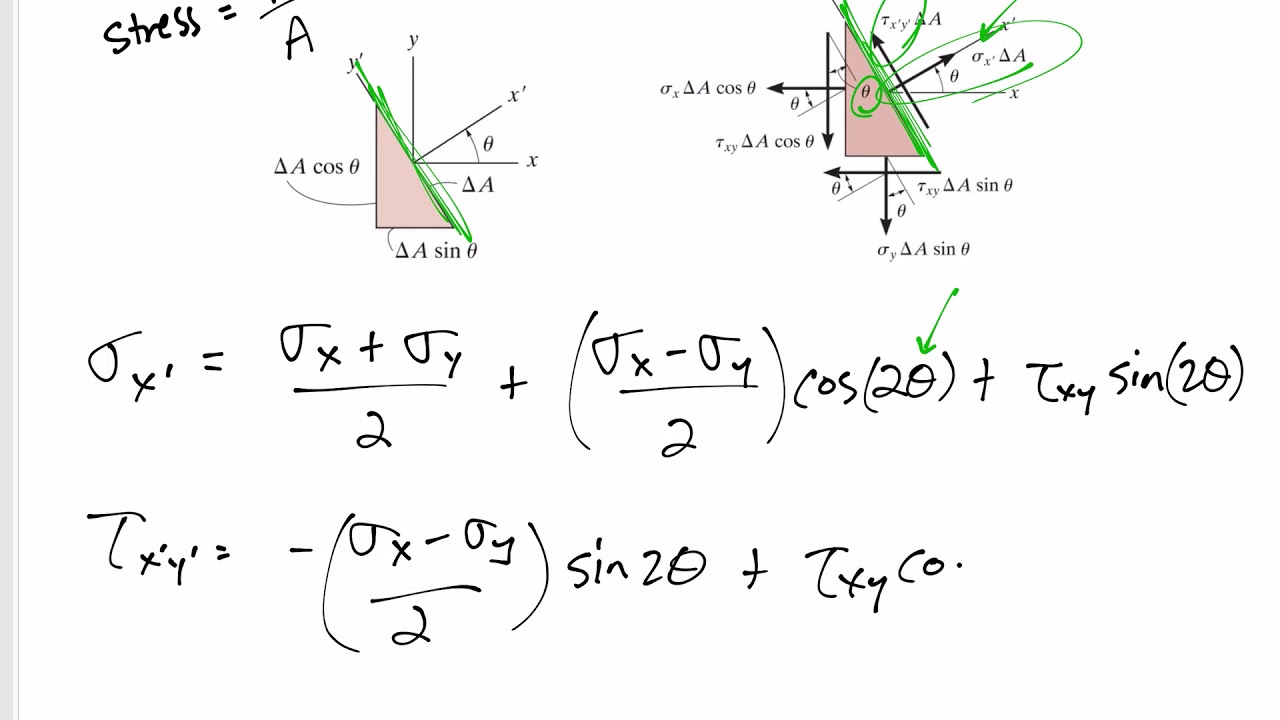
Mechanics of Materials - 2D Plane stress transformation equations
5.0 / 5 (0 votes)
