Introduction to Projectile Motion - Formulas and Equations
Summary
TLDRThis video covers essential kinematic equations used to solve projectile motion problems. It explains the four key equations for motion with constant acceleration and delves into different projectile trajectories: horizontal launches, angled launches, and launches from elevated positions. The video demonstrates how to calculate displacement, velocity, time, range, and angle for each scenario, utilizing equations such as d = v_0t + (1/2)at^2 and the range formula R = (v^2 * sin(2θ)) / g. Viewers also learn how to avoid common mistakes in calculations and how to apply these equations effectively.
Takeaways
- 📐 The displacement of an object moving at constant speed is equal to velocity multiplied by time.
- 🚀 For constant acceleration, the final speed is equal to the initial speed plus acceleration times time.
- 📊 The square of the final speed is equal to the square of the initial speed plus two times acceleration multiplied by displacement.
- 🕰️ Displacement can be found using the average speed (initial speed plus final speed divided by two) multiplied by time.
- 📏 Displacement (D) is equal to initial velocity times time plus half the acceleration times the square of time.
- 📉 In projectile motion, separate calculations for the horizontal (X) and vertical (Y) directions are needed.
- 🟰 In horizontal projectile motion, the height (H) can be calculated using H = 1/2 * acceleration * time^2.
- 🧮 To find the range of a projectile, use the equation Range = velocity * time in the X direction.
- 🎯 The total time of flight for a projectile launched at an angle is 2 * V * sin(Theta) / g.
- 📐 The maximum height of a projectile is given by the formula Height = (V^2 * sin^2(Theta)) / (2 * g).
Q & A
What are the basic kinematic equations for constant speed motion?
-For constant speed motion, the basic kinematic equation is displacement equals velocity multiplied by time.
List the four key equations for motion with constant acceleration.
-The four key equations for motion with constant acceleration are: 1) final speed equals initial speed plus acceleration times time, 2) the square of the final speed equals the square of the initial speed plus 2 times acceleration times displacement, 3) displacement equals average speed times time (where average speed is the sum of initial and final speeds divided by two), and 4) displacement equals initial velocity times time plus half of acceleration times the square of time.
What is the difference between displacement and distance?
-Displacement and distance are the same if an object moves in one direction without changing direction. If the object changes direction, displacement and distance are not the same. Displacement is the straight-line distance from the initial to the final position, while distance is the total path length traveled.
What are the three types of trajectories in projectile motion?
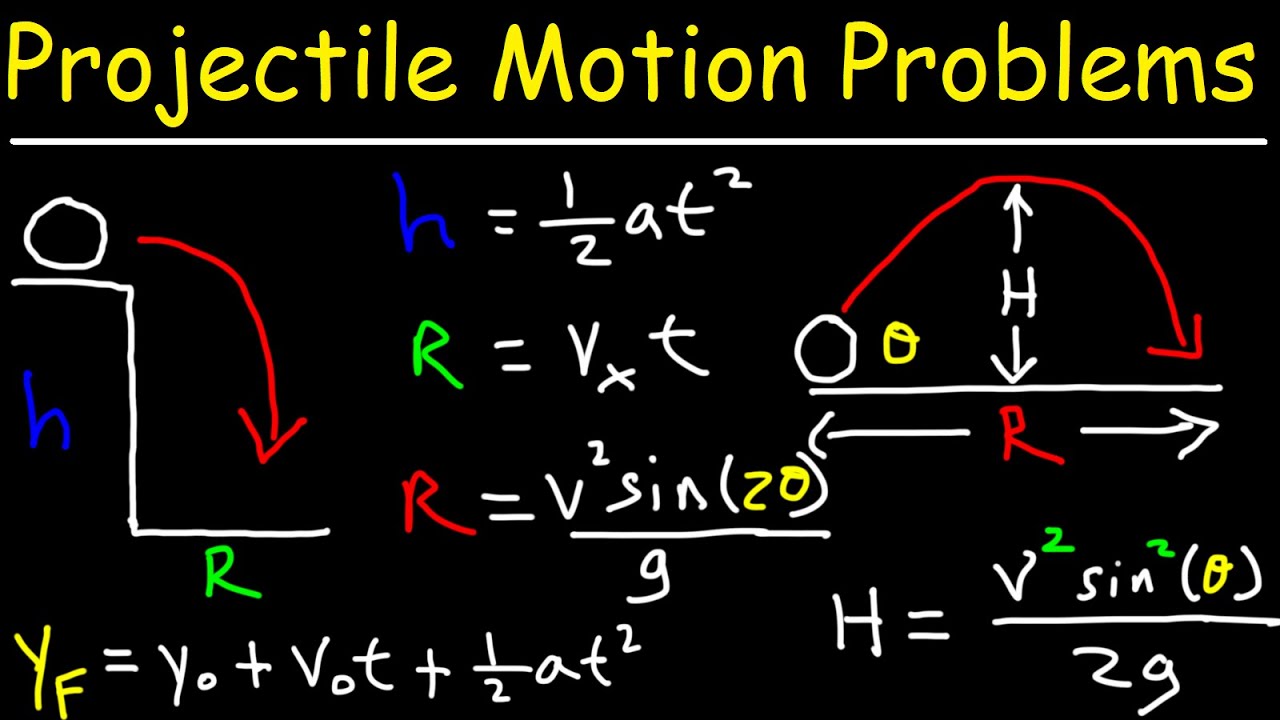
-The three types of trajectories in projectile motion are: 1) horizontal launch from a height (like off a cliff), 2) launched at an angle from ground level, and 3) launched at an angle from an elevated position.
How can you calculate the height of a cliff if an object is projected horizontally and falls off?
-To calculate the height of a cliff, use the equation H equals 1/2 times acceleration due to gravity times time squared (H = 1/2 * g * t^2), where time is the time it takes for the object to hit the ground.
What is the formula to calculate the range of a projectile launched horizontally from a cliff?
-The formula to calculate the range (horizontal distance traveled) of a projectile launched horizontally from a cliff is range equals initial horizontal velocity times time (R = Vx * t).
How do you find the speed of a ball just before it hits the ground in projectile motion?
-To find the speed of a ball just before it hits the ground, you need to calculate both the horizontal velocity (which remains constant) and the vertical velocity using the equation VY final equals initial vertical velocity plus acceleration due to gravity times time.
What is the relationship between the angle of launch, initial velocity, and maximum height for a projectile launched at an angle from the ground?
-The maximum height of a projectile launched at an angle from the ground is given by the equation H equals initial velocity squared times sin^2(angle) divided by 2 times gravity (H = V^2 * sin^2(Theta) / 2G).
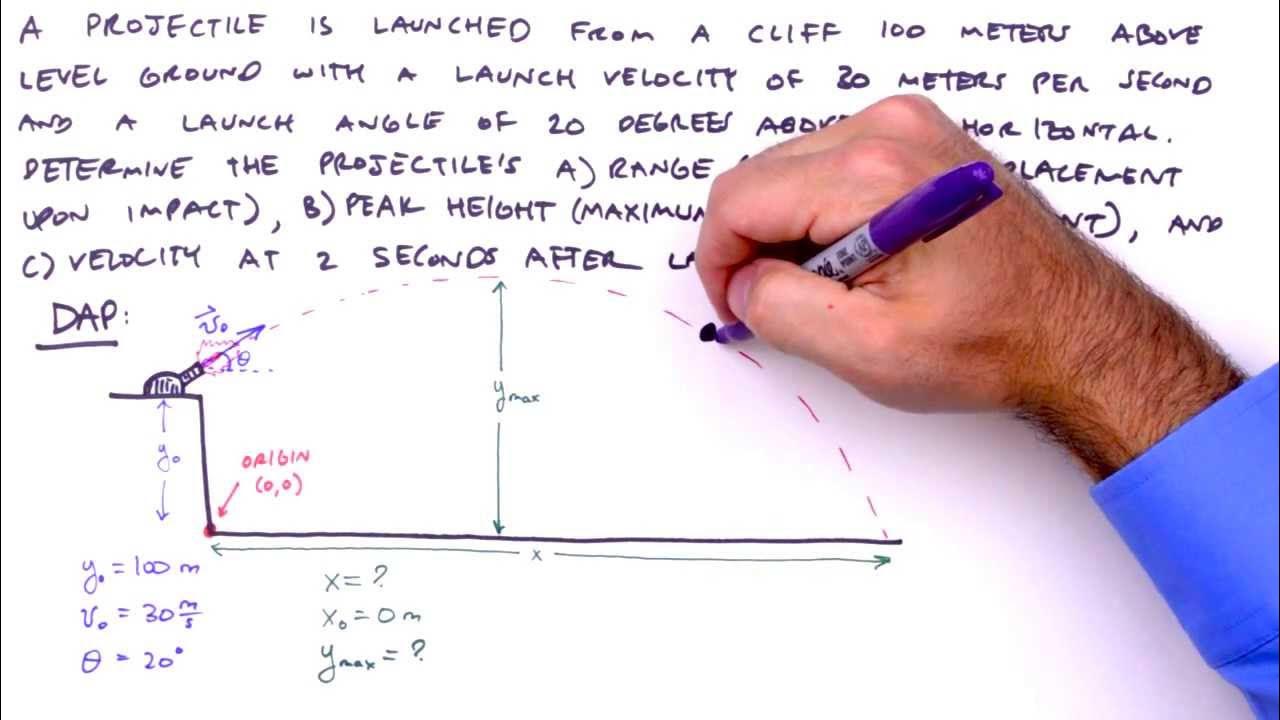
How can you determine the time it takes for a projectile to hit the ground when launched at an angle from an elevated position?
-The time it takes for a projectile to hit the ground when launched at an angle from an elevated position can be found using the quadratic formula to solve the equation Y final equals initial height plus initial vertical velocity times time plus half of gravity times time squared, set to zero since Y final is ground level.
What is the equation to calculate the range of a projectile launched at an angle from an elevated position?
-The range of a projectile launched at an angle from an elevated position is calculated using the equation range equals initial horizontal velocity times time (R = Vx * t), where time is the time it takes to hit the ground and initial horizontal velocity is the horizontal component of the initial velocity (Vx = V * cos(Theta)).
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)