Lamps/Streetlights CodeSignal Coding Question - Sweep Line Algorithm
Summary
TLDRThis video tutorial addresses a challenging coding problem from CodeSignal involving lamps or streetlights. The problem requires determining how many lamps illuminate each of a series of benches located along a coordinate line. The standard approach, using a hashmap, falls short due to time constraints, leading to a Time Limit Exceeded (TLE) error. Instead, the video introduces a line sweep algorithm, an efficient method for handling such spatial problems. The algorithm involves creating events for when lamps start or stop illuminating and when benches are encountered, sorting these events, and then processing them in a specific order to count the illuminating lamps at each bench's location. The tutorial provides a detailed walkthrough of implementing this algorithm in Java, complete with code examples and a discussion of the algorithm's time and space complexity.
Takeaways
- 😀 The video discusses a common coding signal question involving lamps or street lights, which is notoriously difficult due to its time constraints and non-standard approach compared to typical hashmap solutions.
- 🕵️♂️ The suggested approach to solving the problem is a line sweep algorithm, which is different from the usual hashmap solutions often used for signal questions.
- 🚦 The problem involves a long coordinate line with multiple lamps, each having an illuminating range, and benches placed at specific coordinates along the line.
- 📊 The goal is to determine how many lamps are illuminating each bench and return this as an array, where each index corresponds to the number of lamps illuminating the respective bench.
- ⏱️ The challenge is to efficiently process this information given the potentially large number of lamps, benches, and the extensive coordinate line, which could lead to a time limit exceeded (TLE) error.
- 🛠️ A line sweep algorithm is used by creating events for when lamps start and stop illuminating and when benches are encountered, sorted in a priority queue based on the time and type of event.
- 🔄 The events are processed in a specific order: lamp on, bench encounter, and then lamp off, to ensure the correct count of illuminating lamps at each bench.
- 💡 The algorithm iterates over relevant points (lamp start/stop and bench locations) rather than all possible coordinates, making it feasible within the time constraints.
- 💻 The video provides a step-by-step coding example in Java, demonstrating how to implement the line sweep algorithm, including the use of a priority queue and a comparator for event ordering.
- 📈 The time complexity of the algorithm is O(n log n) due to the insertion of events into the priority queue, and the space complexity is O(n) for the size of the priority queue.
Q & A
What is the main challenge in solving the CodeSignal 'lamps' problem?
-The main challenge in solving the CodeSignal 'lamps' problem is the notorious difficulty due to its time constraints and the fact that it doesn't fit the typical hashmap solution approach that many question fours have. This often leads to a Time Limit Exceeded (TLE) issue.
What algorithm is suggested to solve the 'lamps' problem efficiently?
-A line sweep algorithm is suggested to solve the 'lamps' problem efficiently, which involves moving over a timeline and keeping track of the number of lamps illuminating the current point.
How does the line sweep algorithm handle the events in the 'lamps' problem?
-The line sweep algorithm handles events by considering three types of events: lamp starting to illuminate, lamp stopping to illuminate, and encountering a bench. It processes these events in a priority queue with a specific ordering to ensure the correct count of illuminating lamps at each bench.
Why is it important to maintain a specific order when processing events in the line sweep algorithm?
-Maintaining a specific order when processing events is crucial because it ensures that the count of illuminating lamps is accurate when a bench event is processed. For example, a lamp starting to illuminate should be processed before the corresponding bench event to correctly account for its illumination.
How does the algorithm handle overlapping events at the same coordinate?
-The algorithm handles overlapping events by ensuring that events are processed in a specific order: lamp starting to illuminate, encountering a bench, and then lamp stopping to illuminate. This order is crucial for maintaining the correct count of illuminating lamps at each bench.
What data structure is used to store and process events in the line sweep algorithm?
-A priority queue is used to store and process events in the line sweep algorithm. The priority queue is ordered based on the time of the event and then by the type of event, ensuring that events are processed in the correct order.
How is the final result array constructed in the 'lamps' problem?
-The final result array is constructed by iterating through the events in the priority queue, updating the count of illuminating lamps, and storing the count in the result array each time a bench event is encountered.
Why is it necessary to tag the bench index in the event when using a priority queue?
-Tagging the bench index in the event is necessary because the order in which events are processed by the priority queue may not match the order of benches in the input array. This ensures that the correct number of illuminating lamps is associated with each bench, regardless of the order in which events are processed.
What is the time complexity of the line sweep algorithm as described in the script?
-The time complexity of the line sweep algorithm is O(n log n), where n is the number of events. This is due to the events being added once into the priority queue and then processed.
How does the algorithm ensure that the illuminating lamp count is accurate for each bench?
-The algorithm ensures accuracy by processing events in a priority queue, updating the count of illuminating lamps each time a lamp starts or stops illuminating, and recording the count each time a bench event is processed.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

The Mercury Vapor Lamp 1901

Solving My Google Phone Interview Question
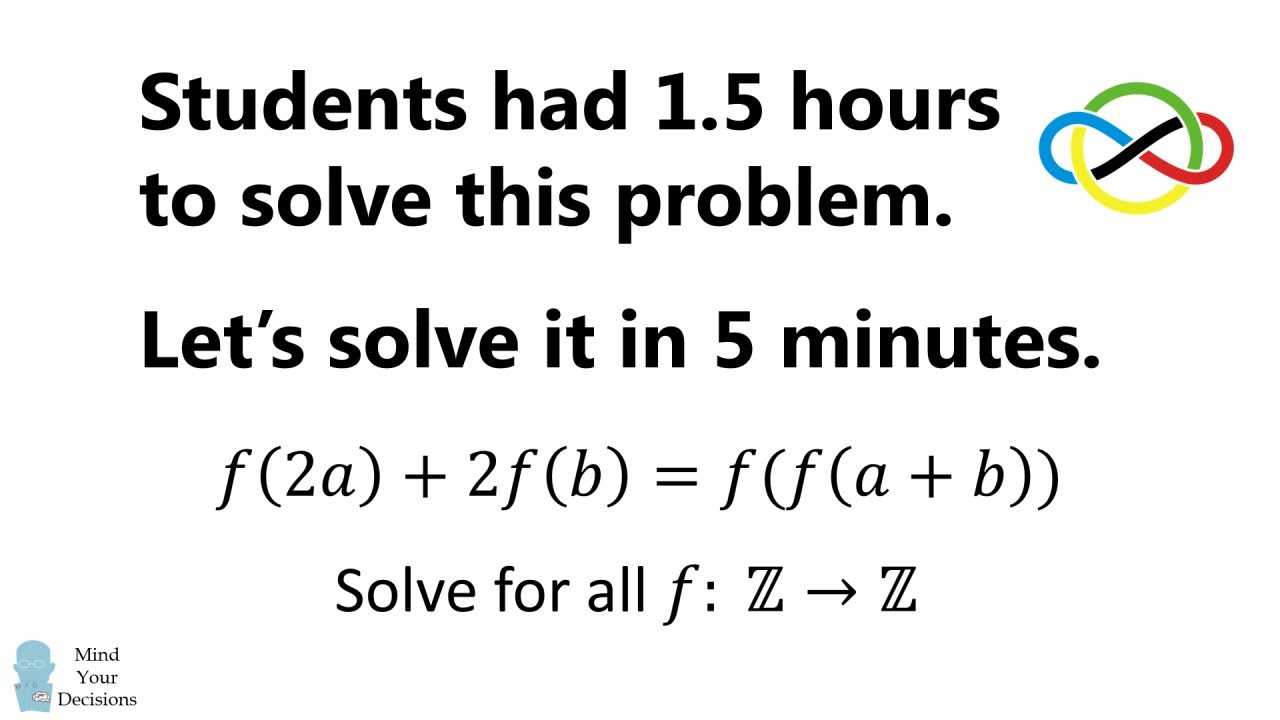
Solving An Insanely Hard Problem For High School Students

Solusi HTML:5 Tidak Berfungsi di Visual Studio Code: Panduan Lengkap!

Delete Nodes From Linked List Present in Array - Leetcode 3217 - Python

Introduction to Greedy Algorithms | GeeksforGeeks
5.0 / 5 (0 votes)
