Resistencia de Materiales
Summary
TLDREste vídeo ofrece una introducción a los conceptos fundamentales de la ingeniería estructural, abarcando desde matemáticas básicas como trigonometría y teorema de Pitágoras, hasta la física con la introducción a vectores y descomposición de vectores en el plano cartesiano. Se explican las propiedades de los vectores y cómo se aplican en el estudio de la estática, incluyendo las tres leyes fundamentales del equilibrio y la importancia de los momentos en la mecánica de sólidos. El objetivo es ayudar a los ingenieros a comprender plenamente cómo funcionan las estructuras y a mejorar su retroalimentación en el uso de software estructural.
Takeaways
- 🔍 El video comienza explorando cómo las estructuras en el software funcionan, sugiriendo que para comprender completamente cómo funcionan, es necesario entender los principios fundamentales de la mecánica clásica, la teoría de la elasticidad y la teoría de la plasticidad.
- 🏗️ Se destaca la importancia de entender cómo el acero y el hormigón, dos elementos estructurales clave en la construcción, no solo no se deforman de la misma manera, sino que también trabajan conjuntamente bajo los estados límites últimos de rotura y de servicio.
- 📚 Se enfatiza la necesidad de regresar a conceptos básicos, como la trigonometría, el vector y las leyes del equilibrio, para realizar un cálculo estructural adecuado.
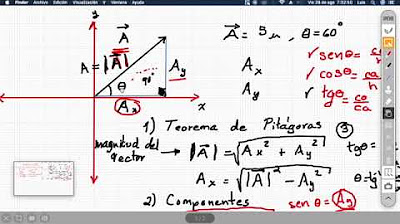
- 📐 Se explica la relevancia de la trigonometría en el estudio de triángulos, especialmente el triángulo rectángulo, y cómo Pitágoras contribuyó con su teorema para relacionar los lados de dicho triángulo.
- 📈 Se introducen las identidades trigonométricas fundamentales: seno, coseno y tangente, y se describe cómo se relacionan con los ángulos y los lados de un triángulo rectángulo.
- 🧭 Se discute la importancia de los vectores en la física, incluyendo sus cuatro propiedades principales: magnitud, dirección, sentido y punto de aplicación.
- 📏 Se describe cómo se puede descomponer un vector en sus componentes en los ejes cartesianos x e y, utilizando las identidades trigonométricas para facilitar el cálculo estructural.
- ⚖️ Se presentan las tres leyes fundamentales de la estática: la suma de las fuerzas horizontales, la suma de las fuerzas verticales y la suma de los momentos en un punto, que son esenciales para el equilibrio de los cuerpos.
- 🔧 Se menciona brevemente la introducción a la mecánica de sólidos y la resistencia de materiales, con énfasis en los estados límites últimos de servicio y rotura, que son cruciales para la retroalimentación en el ámbito estructural.
Q & A
¿Qué es la retroalimentación en el marco del ámbito estructural?
-La retroalimentación en el ámbito estructural se refiere a un proceso de aprendizaje y comprensión donde se revisan y se analizan los principios fundamentales de la mecánica clásica, la teoría de la elasticidad y la teoría de la plasticidad para entender cómo funcionan las estructuras de hormigón armado.
¿Cuáles son los elementos estructurales principales mencionados en el guion que trabajan conjuntamente en una estructura de hormigón armado?
-Los elementos estructurales principales mencionados son el acero y el hormigón, que no se deforman de la misma manera pero sí trabajan conjuntamente bajo los estados límites últimos de rotura y estados límites últimos de servicio.
¿Qué áreas de estudio son fundamentales para realizar un cálculo estructural según el guion?
-Las áreas de estudio fundamentales para realizar un cálculo estructural son la trigonometría, la física y la aplicación de las tres leyes del equilibrio.
¿Qué es el teorema de Pitágoras y cómo se relaciona con los triángulos rectángulos?
-El teorema de Pitágoras es una fórmula matemática que se aplica a los triángulos rectángulos, estableciendo que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Cuáles son las tres identidades trigonométricas principales mencionadas en el guion?
-Las tres identidades trigonométricas principales mencionadas son el seno, el coseno y la tangente, que se definen en relación con los catetos y la hipotenusa de un triángulo rectángulo.
¿Qué propiedades poseen los vectores según lo explicado en el guion?
-Los vectores poseen cuatro propiedades principales: magnitud (módulo), dirección, sentido y punto de aplicación.
¿Qué es el plano cartesiano y cómo se relaciona con la descomposición de vectores?
-El plano cartesiano es un sistema de coordenadas bidimensional formado por dos ejes, x e y, que se utiliza para descomponer vectores en sus componentes en x e y, facilitando su análisis y suma.
¿Qué son las tres leyes del equilibrio mencionadas en el guion y cómo se aplican en la estática?
-Las tres leyes del equilibrio son: 1) la sumatoria de las fuerzas horizontales es igual a cero, 2) la sumatoria de las fuerzas verticales es igual a cero y 3) la sumatoria de los momentos alrededor de un punto es igual a cero. Estas leyes son fundamentales para analizar el equilibrio de cuerpos en la estática.
¿Qué es un momento en el contexto de la estática y cómo se calcula?
-Un momento en la estática es una medida del tendencia de una fuerza a causar la rotación alrededor de un punto o eje, y se calcula como la fuerza multiplicada por la distancia perpendicular desde el punto de aplicación de la fuerza hasta el eje de rotación.
¿Cuáles son los estados límites últimos de rotura y de servicio mencionados en el guion y qué significan?
-Los estados límites últimos de rotura y de servicio son conceptos en ingeniería estructural que definen los puntos en los que una estructura deja de ser capaz de soportar las cargas aplicadas sin sufrir daño estructural o fallar completamente.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)