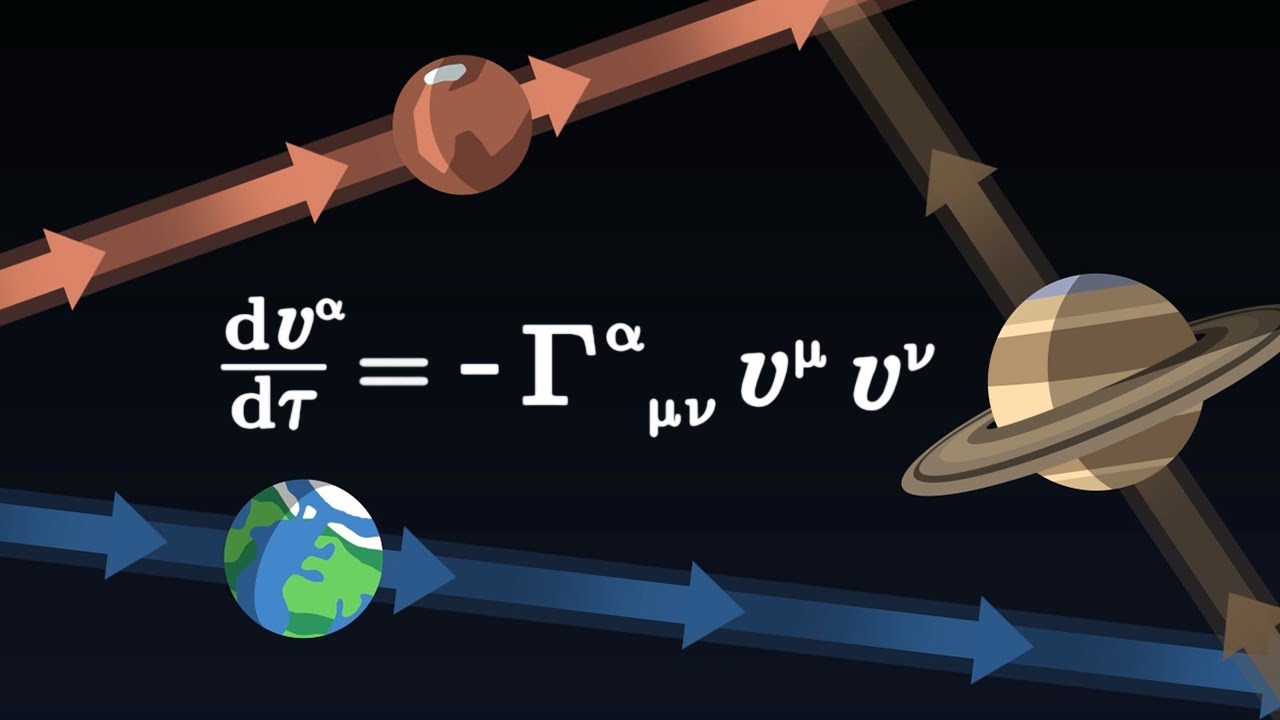The Maths of General Relativity (5/8) - Curvature
Summary
TLDRIn this episode of Science Clique, the focus is on the mathematics of general relativity, specifically curvature. The video explains how the metric tensor measures distances in space-time and how geodesics predict object movement without assuming space-time geometry. It introduces the concept of space-time curvature affecting object trajectories and uses the curvature of a sphere to illustrate gravitational effects. The video then defines curvature mathematically, explaining how vector transport on different surfaces like planes and spheres results in different orientations, indicating curvature. It introduces the Riemann curvature tensor, the Ricci tensor, and the Ricci scalar, which describe surface curvature in various ways. Examples of Minkowski space-time and a sphere illustrate these concepts, showing how curvature affects geodesic behavior.
Takeaways
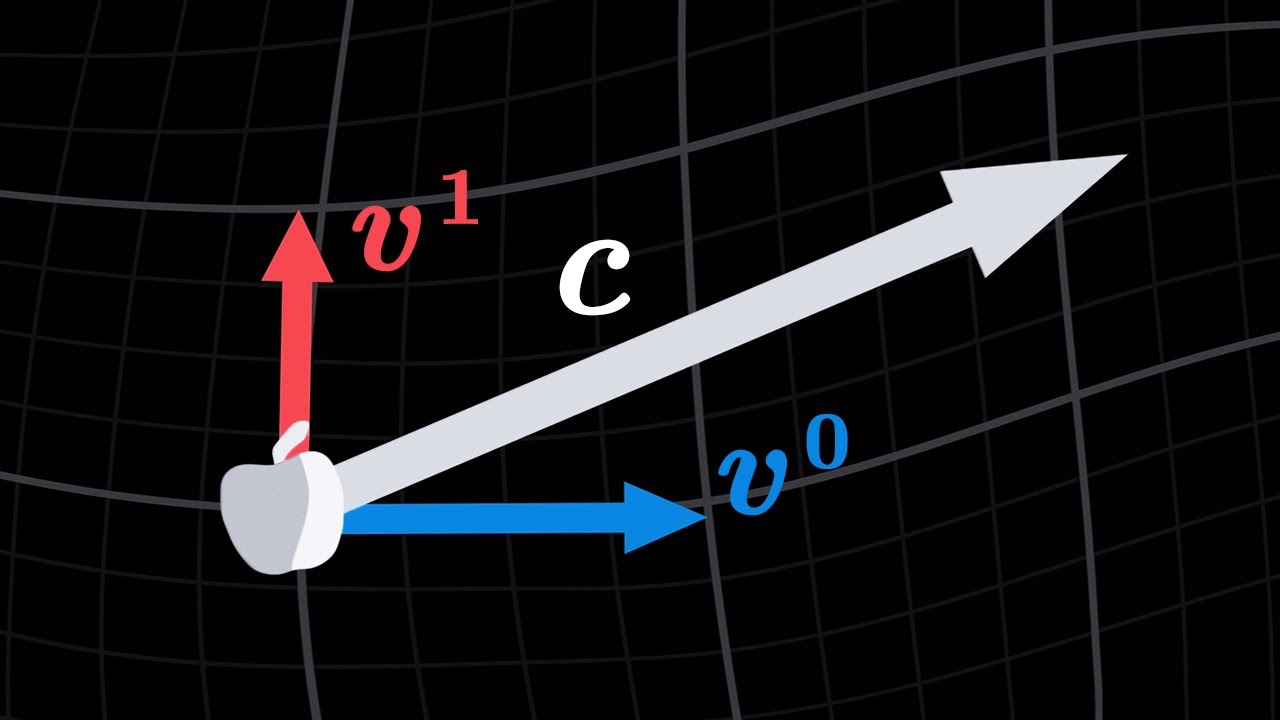
- 🌌 The metric tensor is essential in general relativity for measuring distances in space-time and predicting the movement of objects.
- 🔄 General relativity does not assume a flat geometry of space-time; it can model both flat and curved geometries.
- 🌐 Curvature of space-time affects the trajectories of objects, such as parallel geodesics on a sphere converging towards each other.
- 📏 Curvature is defined by the transport of vectors along different paths on a surface, affecting their final orientation.
- 📊 The Riemann curvature tensor is a mathematical representation of curvature, describing how basis vectors change when transported along different coordinates.
- 🔢 The Riemann tensor has 16 components in a 2-dimensional space, and 256 components in a 4-dimensional space-time, making it complex to handle.
- 📋 The Ricci tensor simplifies the description of curvature by focusing on the diagonal components of the Riemann tensor, representing volume changes along the surface.
- 🔑 The Ricci scalar is a single number that characterizes the average curvature in all directions for symmetric surfaces like a sphere.
- 🌐 In an empty space-time with the Minkowski metric, the curvature tensor and Ricci scalar vanish, indicating a flat space-time with no curvature.
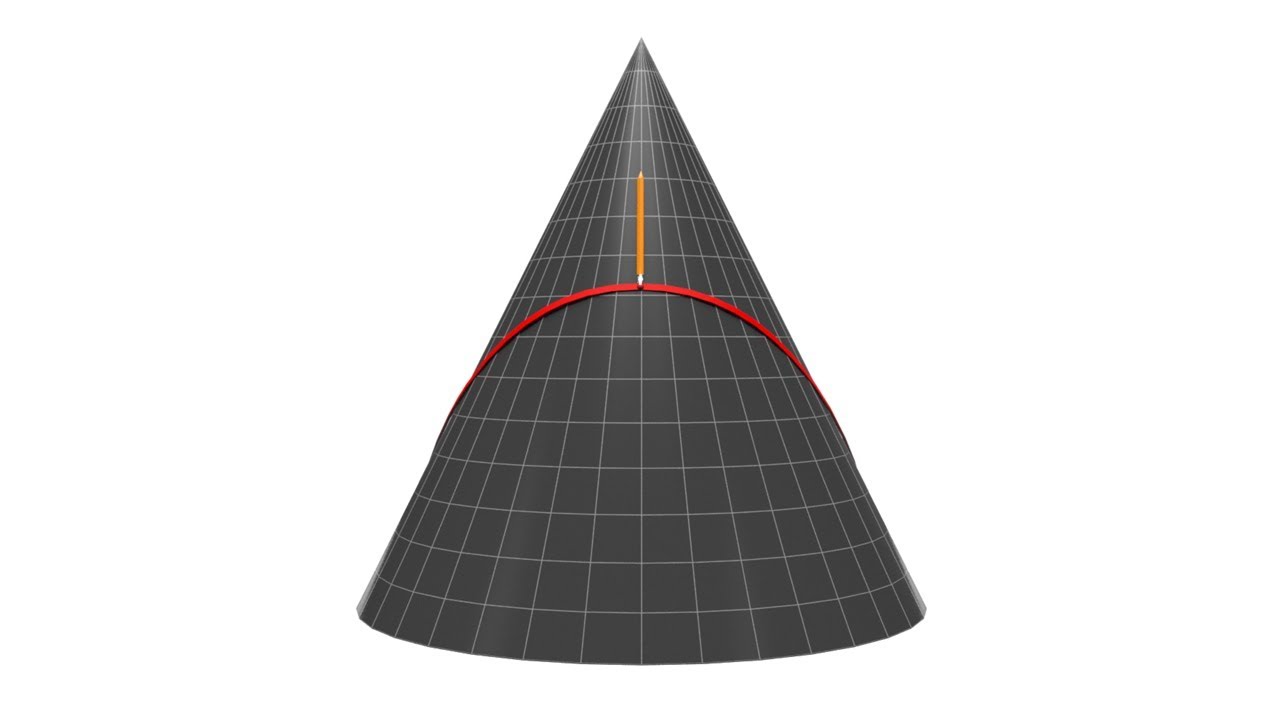
- 🌍 On the surface of a sphere, the curvature is positive, causing parallel geodesics to approach each other, and the curvature decreases as the sphere's radius increases.
Q & A
What is the significance of curvature in the context of general relativity?
-In general relativity, curvature is crucial as it describes the geometry of space-time and influences the trajectories of objects within it. Curvature is what allows for the modeling of gravity, where the presence of mass bends space-time, affecting the paths of objects.
How does the geometry of space-time affect the movement of objects?
-The geometry of space-time, whether flat or curved, affects the movement of objects by determining the geodesics they follow. In a curved space-time, such as near massive objects, the paths of objects can bend, leading to phenomena like gravitational attraction.
What is a geodesic and why is it important in understanding space-time?
-A geodesic is the shortest path between two points in space-time. It is important because it represents the natural path that a free-falling object would take in the presence of a gravitational field, which is a direct consequence of the curvature of space-time.
How does the curvature of a surface affect the transportation of vectors?
-The curvature of a surface affects the transportation of vectors by altering their orientation depending on the path taken. On a flat surface, the final orientation is independent of the path, but on a curved surface, the order of transportation (right then up or up then right) results in different orientations.
What is the Riemann curvature tensor and why is it important?
-The Riemann curvature tensor is a mathematical object that describes the curvature of a surface in all possible directions. It is important because it fully encapsulates the geometric properties of the space-time, allowing for a comprehensive understanding of how it curves and influences the motion of objects.
How can the curvature of a surface be quantified mathematically?
-The curvature of a surface can be quantified mathematically by calculating the Riemann curvature tensor, which involves taking derivatives of basis vectors and comparing the results of transporting these vectors along different paths on the surface.
What is the Ricci tensor and how does it simplify the description of curvature?
-The Ricci tensor is a derived quantity from the Riemann curvature tensor that simplifies the description of curvature by reducing the number of components needed to describe it. It measures how volumes change along the surface's curvature and is particularly useful for calculating the average curvature in symmetric spaces.
What is the Ricci scalar and how does it relate to the curvature of space-time?
-The Ricci scalar is a single number derived from the Ricci tensor that characterizes the average curvature of space-time in all directions. It is a scalar quantity that provides a concise measure of the overall curvature, especially useful for symmetric spaces like a sphere.
How does the Minkowski metric relate to the curvature of space-time?
-The Minkowski metric describes an empty space-time that is flat, with no curvature. It has constant components that do not depend on coordinates, leading to zero derivatives and thus no curvature, as indicated by the vanishing of the Riemann, Ricci tensors, and the Ricci scalar.
What can be inferred about the curvature of a sphere from the script?
-From the script, it can be inferred that the curvature of a sphere is positive, causing parallel geodesics to approach each other. Additionally, the curvature decreases as the radius of the sphere increases, making the surface flatter for larger spheres.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)