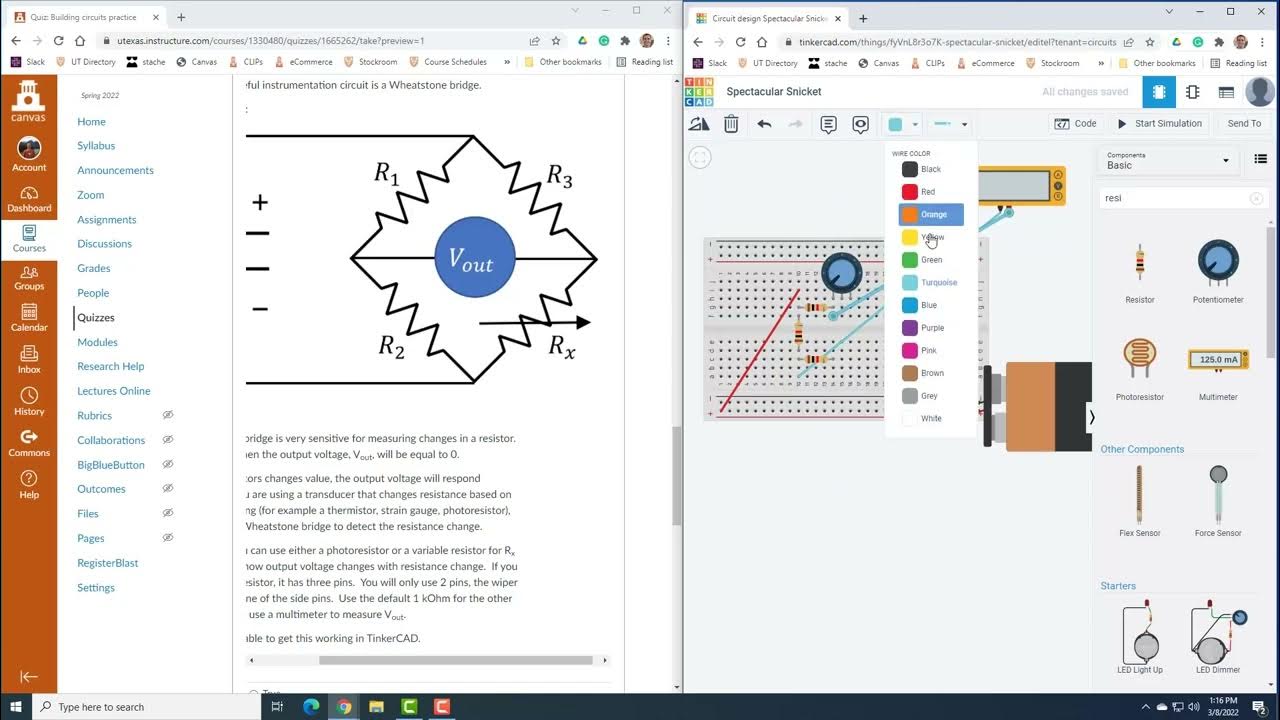
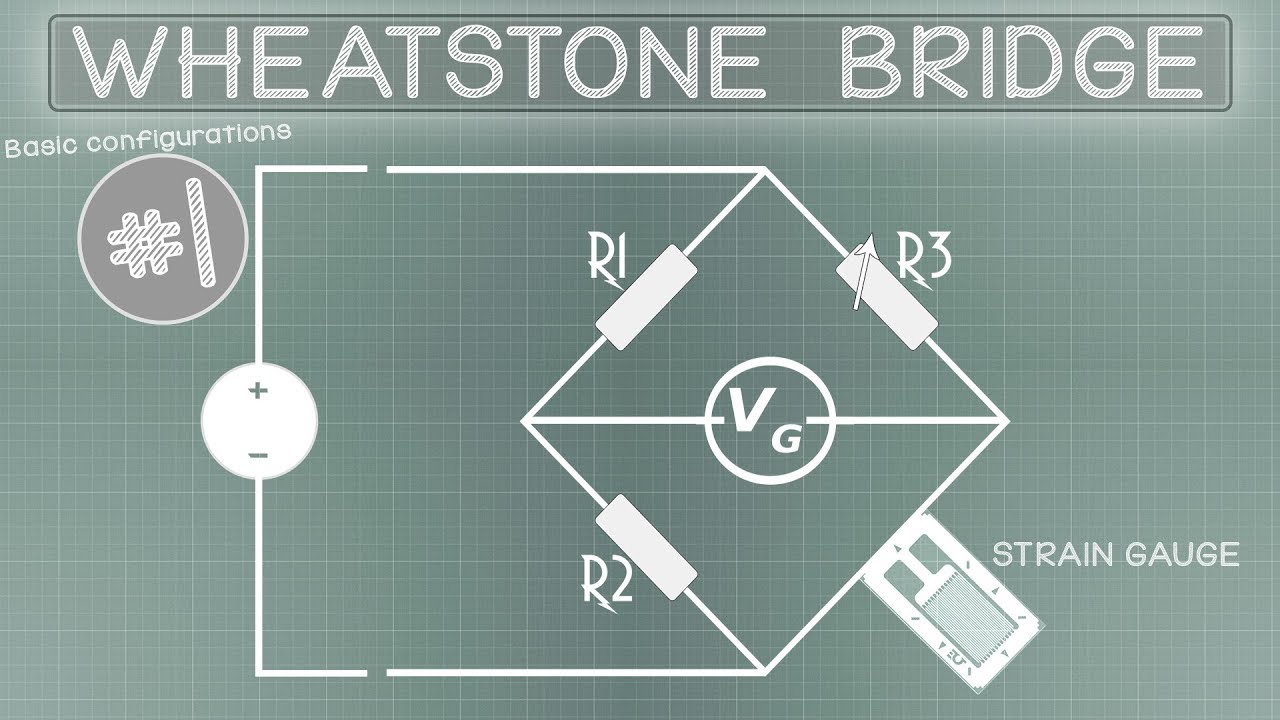
Rangkaian Jembatan Wheatstone dan Rangkaian Delta Star
Summary
TLDRThe video script discusses the Wheatstone bridge, a circuit used to measure unknown resistances, and introduces Charles Wheatstone who invented it. It explains how to find the equivalent resistance of a complex circuit by checking certain conditions and converting the circuit into a series or parallel configuration if necessary. The script also covers the Delta-Y (or Delta-Star) transformation, another method for solving complex circuits when the Wheatstone bridge conditions aren't met. It provides step-by-step calculations to determine the total equivalent resistance, engaging viewers with practical examples and mathematical solutions.
Takeaways
- 😀 The script discusses the Wheatstone bridge circuit and its method for finding the equivalent resistance in complex networks.
- 🔍 It explains the condition for the Wheatstone bridge to work, which is that the product of the resistances R1 and R3 must equal the product of R2 and R4.
- 🛠️ If the condition is met, the current through the fifth resistor (R5) is zero, simplifying the circuit to a series of R1 and R2, and R3 and R4.
- 🔄 The script also covers the Delta-Star transformation, an alternative method used when the Wheatstone bridge condition is not met.
- 📚 The Delta-Star method involves converting a delta configuration of resistors into a star configuration, and vice versa, to calculate the equivalent resistance.
- 🔢 The process of finding the total equivalent resistance involves calculating the sum of series resistances and then converting them into a parallel resistance.
- 📉 The script provides an example problem to demonstrate the calculation of the total equivalent resistance using the Wheatstone bridge method.
- 📝 It emphasizes the importance of checking the condition for the Wheatstone bridge before proceeding with the calculation.
- 🔎 The script explains how to calculate individual resistances (Ra, Rb, Rc) in the Delta-Star method and their relationship to the original resistors.
- 📊 The final step in the Delta-Star method involves finding the parallel resistance by adding the calculated individual resistances and simplifying the expression.
- 📝 The script concludes with an example calculation of the total equivalent resistance using the Delta-Star method, resulting in an 8-ohm resistance.
Q & A
What is the Wheatstone bridge and who invented it?
-The Wheatstone bridge is a type of electrical bridge used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one with a resistor of unknown value and the other with a resistor of known value. It was invented by Sir Charles Wheatstone.
What is the condition that must be met for the Wheatstone bridge to be balanced?
-For the Wheatstone bridge to be balanced, the product of the resistances in one arm of the bridge must be equal to the product of the resistances in the other arm, i.e., R1 × R3 = R2 × R4.
What happens to the current through the fifth resistor (R5) when the Wheatstone bridge is balanced?
-When the Wheatstone bridge is balanced, the current through the fifth resistor (R5) is zero because there is no voltage difference across it.
How can you find the total equivalent resistance of a Wheatstone bridge when it is balanced?
-When the Wheatstone bridge is balanced, the total equivalent resistance can be found by adding the equivalent resistances of the two series combinations in parallel, which are R1 + R2 and R3 + R4.
What is the Delta-Y (or Delta-Star) transformation and when is it used?
-The Delta-Y (or Delta-Star) transformation is a method used to convert a Delta (mesh) configuration of resistors to a Star (wye) configuration and vice versa. It is used when the Wheatstone bridge condition is not met, to find equivalent resistances for a complex network.
How do you calculate the equivalent resistance for the Delta configuration?
-To calculate the equivalent resistance for the Delta configuration, you use the formulae: Ra = (Rb × Rc) / (Rb + Rc + Ra), and similarly for Rb and Rc, where Ra, Rb, and Rc are the resistances in the Delta configuration.
What is the relationship between the resistances in the Delta and Star configurations?
-The relationship between the resistances in the Delta and Star configurations is given by the transformation equations: Ra = (R1 × R2) / (R1 + R2 + R3), Rb = (R2 × R3) / (R1 + R2 + R3), and Rc = (R1 × R3) / (R1 + R2 + R3).
How do you determine the total equivalent resistance when using the Star configuration?
-When using the Star configuration, the total equivalent resistance is found by adding the individual resistances in parallel, which are calculated from the Delta configuration using the transformation equations.
What is the significance of the condition R1 × R3 ≠ R2 × R4 in a Wheatstone bridge?
-If R1 × R3 ≠ R2 × R4, the Wheatstone bridge is not balanced, and the Delta-Y transformation is required to find the equivalent resistance of the network.
Can you provide an example of how to use the Delta-Y transformation to find the total resistance of a network?
-Yes, if you have a network with resistors R1, R2, R3, and R4, and the condition R1 × R3 ≠ R2 × R4, you would first calculate the equivalent resistances Ra, Rb, and Rc using the Delta-Y transformation, then find the total resistance by adding these in parallel.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)