Jembatan Wheatstone
Summary
TLDRThis video tutorial explains the Wheatstone bridge circuit, its purpose, and how to measure an unknown resistance (RX) by balancing the circuit. It walks through the process of adjusting variable resistances and applying Kirchhoff's laws to achieve balance. With step-by-step demonstrations, the video explains how to configure the bridge to achieve zero current across a specific resistor, ensuring accurate resistance measurement. The tutorial also illustrates how to solve for the unknown resistance using the Wheatstone bridge principle and provides practical examples for users to understand the concept clearly.
Takeaways
- 😀 The Wheatstone Bridge is a circuit used to determine an unknown resistance (RX) by balancing the circuit.
- 😀 The key principle behind the Wheatstone Bridge is balancing the two legs of the circuit to achieve zero current through the galvanometer.
- 😀 To use the Wheatstone Bridge, you need a setup with resistors R1, R2, R3, and R4, along with a variable resistor to adjust until the current through R5 is zero.
- 😀 When the Wheatstone Bridge is balanced, the ratio of resistances in the two legs of the bridge can be written as: R1/R2 = R3/RX.
- 😀 By adjusting the variable resistor (R4) and ensuring the current through the galvanometer (R5) is zero, the unknown resistance (RX) can be calculated.
- 😀 In this specific example, R1 is 10Ω, R2 is 15Ω, and R3 is 28Ω. Solving the equation gives RX = 30Ω.
- 😀 Kirchhoff's Laws are applied to verify the relationships between the resistances and currents in the Wheatstone Bridge circuit.
- 😀 The Wheatstone Bridge is ideal for precisely measuring resistances, especially in situations where accuracy is essential.
- 😀 To check if the Wheatstone Bridge is balanced, the current through the galvanometer (R5) should be zero. This confirms that the resistances are proportionally balanced.
- 😀 The Wheatstone Bridge setup can be used in both theoretical exercises and practical experiments to measure and validate unknown resistances.
- 😀 By analyzing and solving the relationships between the currents and resistances, you can confidently determine the unknown resistance in the circuit.
Q & A
What is the purpose of the Wheatstone Bridge circuit?
-The Wheatstone Bridge circuit is used to determine the unknown resistance (RX) by balancing two legs of a bridge circuit. It helps in precisely measuring resistances by comparing the unknown resistance with known resistances.
How can we find the unknown resistance RX using the Wheatstone Bridge?
-To find the unknown resistance RX, the Wheatstone Bridge is balanced by adjusting the known resistances (R1, R2) until the current through the galvanometer (R5) becomes zero. Once the current is zero, the resistances satisfy the equation R1 * RX = R2 * R3, allowing us to solve for RX.
What happens when the current through R5 is zero in a Wheatstone Bridge?
-When the current through R5 is zero, the Wheatstone Bridge is considered balanced. This indicates that the ratio of resistances in one leg is equal to the ratio in the other leg, allowing for the calculation of the unknown resistance RX.
How is the balancing of the Wheatstone Bridge achieved?
-The balancing is achieved by adjusting one of the known resistances (R2) or by changing the variable resistance until the current flowing through the galvanometer R5 becomes zero, indicating that the bridge is balanced.
What is the significance of Kirchhoff’s laws in the Wheatstone Bridge?
-Kirchhoff’s laws are used to derive the equations for the Wheatstone Bridge. Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL) help in setting up the relations between the currents and voltages at different points in the circuit, which leads to the condition for balancing the bridge.
What is the equation used to calculate the unknown resistance RX in a Wheatstone Bridge?
-The equation used to calculate the unknown resistance RX is derived from the balanced condition: R1 * RX = R2 * R3. By rearranging, RX = (R2 * R3) / R1.
What role does the variable resistance play in the Wheatstone Bridge?
-The variable resistance, often referred to as R3 or sometimes R4 in different setups, is used to fine-tune the circuit and adjust the current through the galvanometer. By adjusting this resistance, the bridge can be balanced, and the unknown resistance can be determined.
How do we check if a Wheatstone Bridge is properly balanced?
-To check if the Wheatstone Bridge is balanced, we observe the current through the galvanometer (R5). When the bridge is balanced, the current through R5 will be zero. At this point, the ratio of the resistances in the two arms of the bridge will satisfy the balance condition.
Can the Wheatstone Bridge be used to measure resistance in a real circuit?
-Yes, the Wheatstone Bridge is commonly used in practical applications to measure resistance accurately, particularly when the resistance value is unknown. It is a standard method for precise measurement of resistances in laboratories and industrial settings.
What happens if the Wheatstone Bridge is not balanced?
-If the Wheatstone Bridge is not balanced, the current through the galvanometer will not be zero. This imbalance indicates that the resistances in the two legs of the bridge are not in the correct ratio, and adjustments are needed to balance the bridge.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
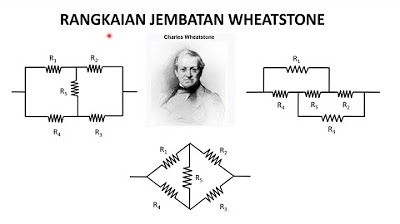
Rangkaian Jembatan Wheatstone dan Rangkaian Delta Star
Practice circuit: making a Wheatstone bridge in TinkerCAD

How To Solve The Wheatstone Bridge Circuit
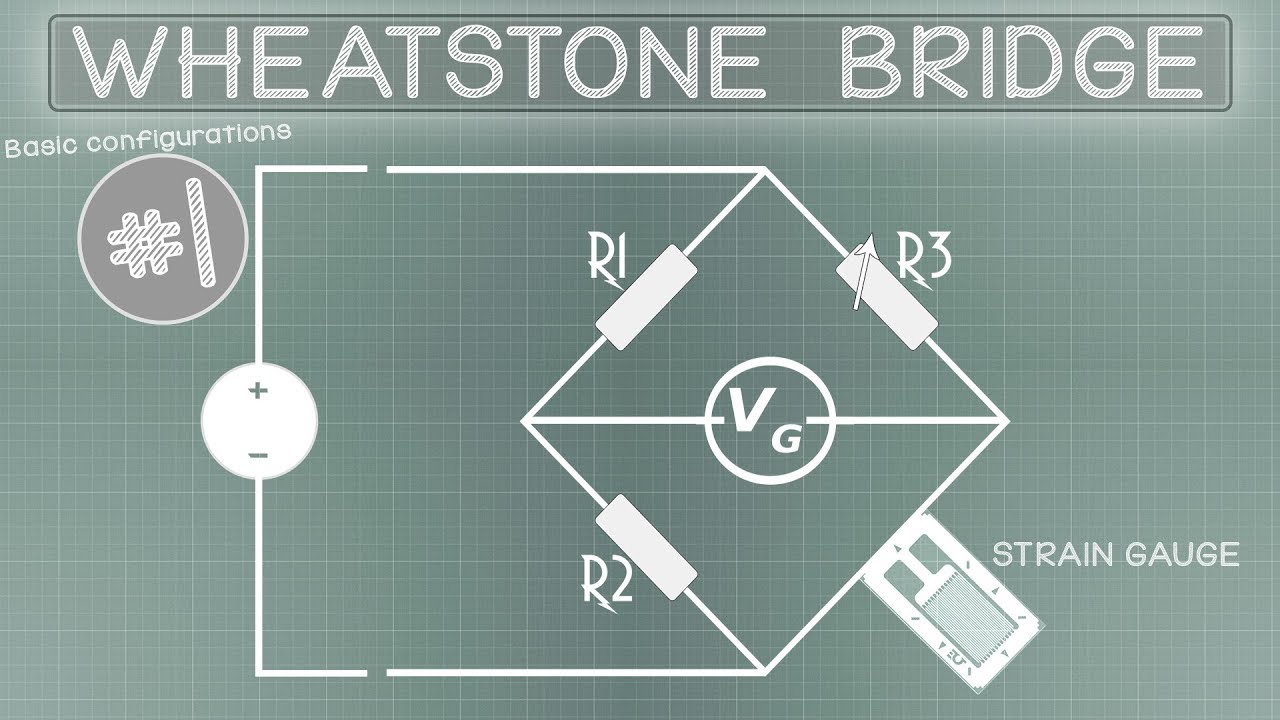
Basic configurations #1 - Wheatstone bridge

3.4 Signal Conditioning for Resistive Sensors - Wheatstone Bridge
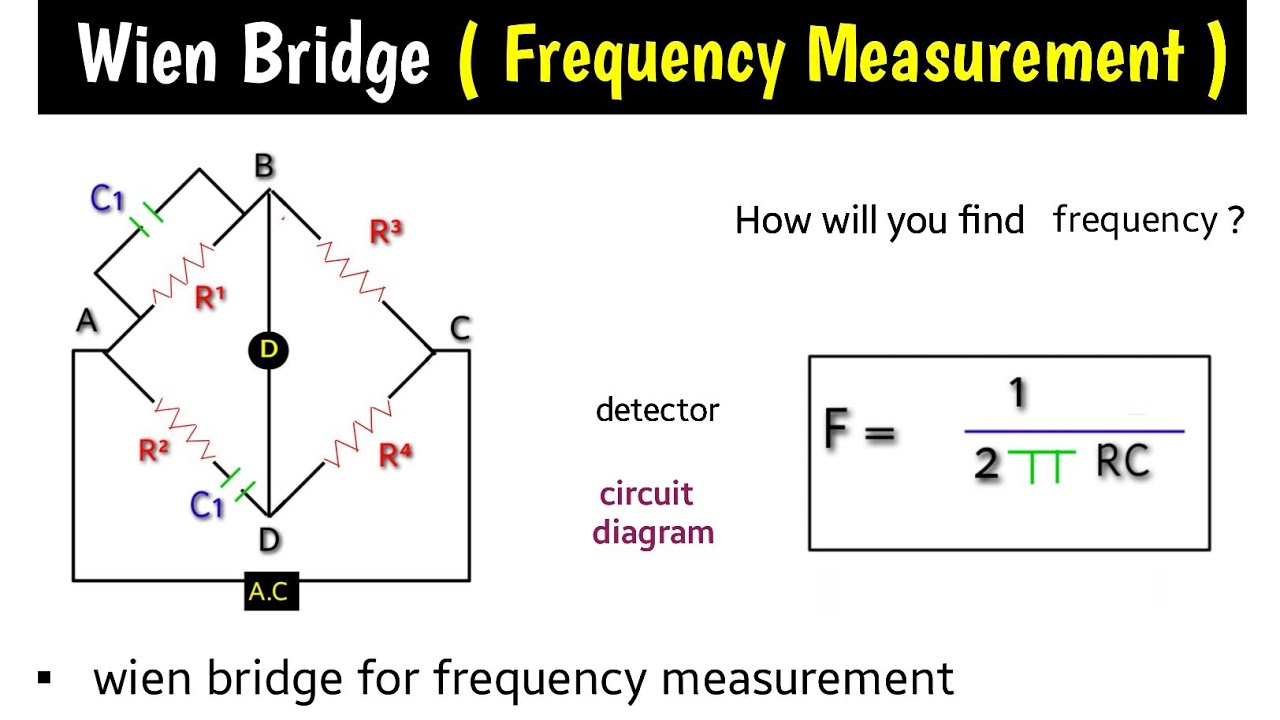
wien bridge |frequency measurement by Wien bridge | Wiens bridge in hindi | wien's bridge | formula
5.0 / 5 (0 votes)