P bahri
Summary
TLDRThis video explains Bernoulli's Principle and the equation of continuity in fluid dynamics. It demonstrates how fluid flows through a tube with varying cross-sectional areas, where the velocity changes based on the size of the tube. The principle highlights conservation of energy, showing that as a fluid's velocity increases in a constricted area, its pressure decreases. The equation of continuity (A1V1 = A2V2) describes the relationship between the flow areas and velocities. The video further explores how energy is conserved through work done on the fluid and how potential and kinetic energy are transferred during flow.
Takeaways
- 😀 Bernoulli's principle states that the flow of a fluid is streamlined, with each particle following the path of the preceding one and having the same velocity.
- 😀 The principle applies to fluids moving through a tube with varying cross-sectional areas, denoted as A1 and A2.
- 😀 The volume of fluid entering A1 per second must equal the volume leaving at A2, based on the conservation of mass.
- 😀 This relationship between the inlet and outlet volumes is governed by the equation of continuity: AV = constant.
- 😀 The velocity of fluid increases when moving through a constricted section of a pipe, i.e., when the cross-sectional area at one end is smaller than the other.
- 😀 The equation of continuity ensures that the product of cross-sectional area (A) and velocity (V) remains constant along the pipe.
- 😀 Bernoulli’s equation incorporates the conservation of energy to explain the relationship between pressure, velocity, and potential energy in a fluid.
- 😀 In a tube with varying cross-sections, the velocity at a narrower section (A2) is greater than at a wider section (A1).
- 😀 The work done per second on the liquid at each section of the tube is related to the change in pressure between the two sections.
- 😀 The net work done per second increases the potential energy and kinetic energy of the fluid as it moves from section A to section B, in line with energy conservation principles.
Q & A
What is Bernoulli's Principle?
-Bernoulli's Principle states that the flow of a fluid is streamlined if every particle of the fluid follows the same path and has the same velocity as its preceding particle.
What does the equation of continuity describe?
-The equation of continuity describes the relationship between the cross-sectional areas of a tube and the velocity of fluid flowing through it. It states that the product of the cross-sectional area and the velocity of the fluid remains constant (AV = constant), assuming no fluid loss.
What happens when the cross-sectional area of a pipe decreases?
-When the cross-sectional area of a pipe decreases, the velocity of the fluid must increase at the constricted end in order to maintain the constant flow rate, as per the equation of continuity.
What does Bernoulli's equation explain in relation to fluid velocity?
-Bernoulli's equation applies the conservation of energy principle to explain that a fluid's velocity increases when moving through a constricted section of a pipe, and this change in velocity is linked to changes in pressure and height.
What is the relationship between the velocity and cross-sectional area at different points in a tube?
-When fluid flows through a tube with varying cross-sectional areas, the velocity of the fluid is inversely proportional to the area. In other words, a smaller cross-sectional area results in a higher velocity, and a larger area results in a lower velocity.
What does the term 'mass of liquid entering per second' refer to?
-The 'mass of liquid entering per second' refers to the amount of fluid mass flowing into a section of the pipe each second. This is balanced by the mass of liquid leaving the pipe at another section.
What is the significance of the work done per second in Bernoulli's Principle?
-The work done per second on the liquid, as described in Bernoulli's Principle, is the difference in pressure (P1 - P2) multiplied by the velocity (V) of the fluid. This work leads to changes in the fluid's potential and kinetic energy.
How does Bernoulli's equation connect to the conservation of energy?
-Bernoulli's equation connects to the conservation of energy by stating that the total mechanical energy of the fluid (kinetic, potential, and pressure energy) remains constant along a streamline, assuming no energy loss.
What happens to the fluid's energy as it flows from point A to point B in a tube of varying cross-section?
-As the fluid flows from point A to point B in a tube with varying cross-sections, the energy transforms between kinetic energy, potential energy, and pressure energy, according to the conservation of energy principle. The work done per second results in changes to the fluid's velocity and height.
Why is the equation of continuity important for understanding fluid dynamics?
-The equation of continuity is important because it helps us understand how fluid velocity and cross-sectional area are related. It ensures that fluid flow is consistent across different sections of a pipe, allowing for predictions about fluid behavior in varying conditions.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

MekFlu #2: Persamaan Bernoulli, Kontinuitas dan Kekekalan Energi

Fluida Dinamis - Konsep Bernoulli - Simple Konsep - Fisika Kelas 11

Dinamika Fluida
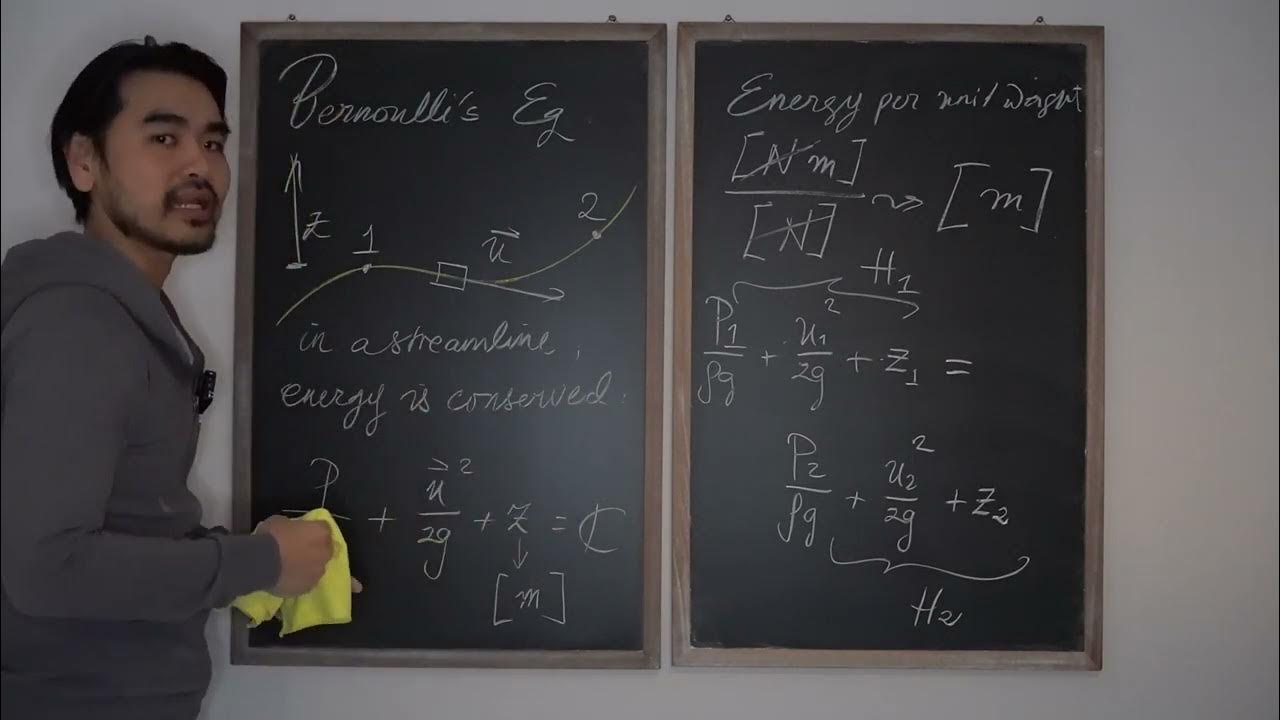
Mekanika Fluida FM01 (Lecture3: 1/8). Persamaan Bernoulli (Pengenalan)

KELOMPOK 11| TPB 9 PENERAPAN FLUIDA DINAMIS PADA INFUS

Mekanika Fluida FM01 (Lecture3: 7/8). Static-Pitot Tube
5.0 / 5 (0 votes)
