Implicit differentiation, what's going on here? | Chapter 6, Essence of calculus

Summary

In this video, the speaker explores two key calculus concepts: implicit differentiation and related rates. Using a circle equation and a ladder problem, they explain how implicit differentiation allows for finding the slope of a tangent line on a curve. The ladder problem illustrates how related rates can link the motion of two variables. Through clear examples, the speaker also ties these concepts together, showing how small changes (dx, dy) impact variables on curves, and introduces the natural log function to demonstrate derivative formulas. The video offers insight into multivariable calculus and the importance of understanding variable interdependence.

Takeaways

• 😀 Implicit differentiation is used to find the slope of tangent lines to curves that are not explicitly functions of one variable, like circles and other implicit curves.
• 😀 A circle with the equation x² + y² = 5² can be used to demonstrate implicit differentiation, where both x and y depend on each other and require special differentiation techniques.
• 😀 To find the slope of the tangent line to the circle at a specific point, we differentiate the equation implicitly, resulting in the formula dy/dx = -x/y.
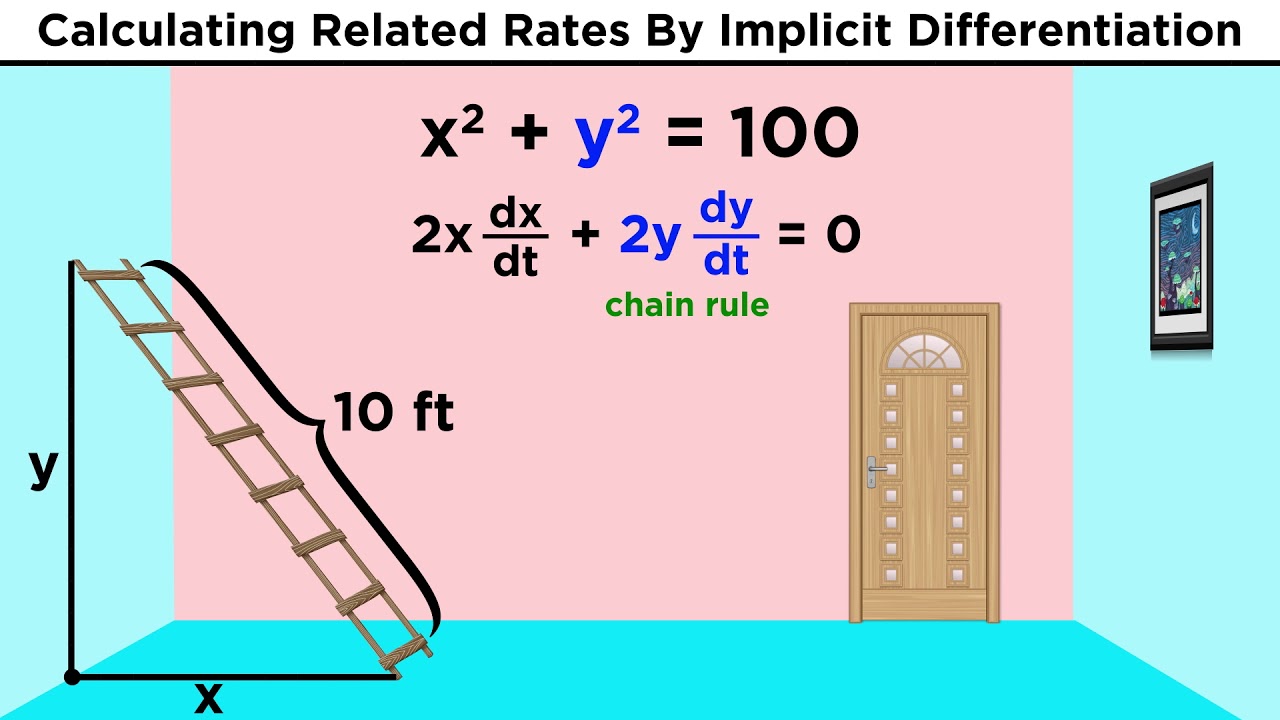
• 😀 Related rates problems, such as a ladder sliding down a wall, involve using implicit differentiation to relate how different quantities change over time, like the top of the ladder and the bottom moving away from the wall.
• 😀 In related rates problems, it's essential to identify quantities dependent on time (like the position of the ladder) and differentiate implicitly to find how their rates of change relate to one another.
• 😀 The Pythagorean theorem x² + y² = 5² is used in both the circle and ladder examples, showing how implicit differentiation can connect geometric and physical problems.
• 😀 In the ladder problem, we calculate the rate at which the bottom of the ladder moves away from the wall using the chain rule and related rates, finding a value of 4/3 meters per second.
• 😀 Implicit differentiation can be applied to various types of curves, not just circles. For example, the equation sin(x * y²) = x can be differentiated implicitly to find how dy/dx relates to x and y.
• 😀 The derivative of natural logarithm functions, such as ln(x), can be found using implicit differentiation by first rearranging the equation and applying the derivative of the exponential function e^y = x.
• 😀 The derivative of ln(x) is 1/x, which is derived by differentiating both sides of the equation e^y = x with respect to x, highlighting the power of implicit differentiation in deriving new formulas.
• 😀 Implicit differentiation is a precursor to multivariable calculus, where functions depend on multiple variables, and understanding how small changes in each variable affect the others is key to solving complex problems.

Q & A

What does the equation x² + y² = 5² represent in the context of the circle?

The equation x² + y² = 5² represents a circle with radius 5, centered at the origin of the xy-plane. All points (x, y) on the circle are equidistant from the origin, and the distance is 5 units, as determined by the Pythagorean theorem.

What is the main challenge when finding the slope of a tangent line to a circle using implicit differentiation?

The main challenge is that, unlike typical functions where x is the input and y is the output, in the case of the circle, both x and y are interdependent variables. This makes it impossible to simply take a derivative as you would with a standard function, so implicit differentiation is used.

What is implicit differentiation?

Implicit differentiation is a technique used to find derivatives of equations where variables are interdependent, rather than one being an input and the other being an output. In this technique, both sides of the equation are differentiated with respect to the variables, and the resulting terms are manipulated to isolate dy/dx.

Why do we include the terms dx and dy when differentiating implicit equations?

We include dx and dy because, in implicit equations, both x and y are treated as variables that can change simultaneously. The terms dx and dy represent tiny changes in x and y, respectively, which are needed to calculate how the value of the equation changes with respect to both variables.

In the ladder problem, what physical scenario is being modeled, and how does it relate to calculus?

The ladder problem models a situation where a 5-meter-long ladder is slipping down a wall, with the top of the ladder falling at a rate of 1 meter per second. The goal is to find the rate at which the bottom of the ladder moves away from the wall. This is a related rates problem, where we use calculus to relate the rates of change of different quantities (the positions of the top and bottom of the ladder).

What does the equation x² + y² = 5² in the ladder problem have in common with the equation for the circle?

Both the ladder problem and the circle problem use the equation x² + y² = 5² to relate the distances involved. In the ladder problem, this equation represents the Pythagorean theorem applied to the ladder, where x is the horizontal distance from the wall, y is the vertical distance from the ground, and the length of the ladder (5 meters) is the constant hypotenuse.

How does implicit differentiation help solve the ladder problem?

Implicit differentiation is used in the ladder problem to relate the rates of change of x and y over time. By differentiating the equation x² + y² = 5² with respect to time, we can find the relationship between dx/dt (the rate at which the bottom of the ladder moves) and dy/dt (the rate at which the top of the ladder falls).

Why does the circle problem feel strange compared to other derivative problems?

The circle problem feels strange because, unlike typical derivative problems where time or a single input variable is involved, the variables x and y in the circle equation are interdependent but not tied to a common variable like time. The derivative involves tiny changes in both x and y, but there's no explicit time component, making the process of differentiating feel unusual.

What does the notation ds represent in the context of the circle?

In the context of the circle, ds represents the change in the value of the function x² + y² as both x and y change. It is used to calculate how much the sum of x² and y² changes when both x and y undergo small changes (dx and dy).

What is the relationship between the slope of a graph and the derivative in multivariable calculus?

In multivariable calculus, the slope of a graph can be interpreted as how the value of a function changes with respect to changes in multiple variables. Implicit differentiation allows us to find how changes in both x and y contribute to the overall change in the function, and this concept extends to more complex functions with multiple inputs and derivatives.

How does implicit differentiation apply to the derivative of the natural logarithm?

Implicit differentiation can be used to derive the formula for the derivative of the natural logarithm. Starting with the equation y = ln(x), we can rearrange it to e^y = x, then differentiate both sides. By applying implicit differentiation, we find that dy/dx = 1/x, which is the derivative of the natural logarithm.