Sudut yang terjadi jika Dua Garis Sejajar dipotong oleh Sebuah Garis

Summary

This educational video explains the various types of angles formed when two parallel lines are intersected by a transversal line. The six main types of angles discussed are: adjacent angles, vertically opposite angles, alternate interior angles, same-side interior angles, alternate exterior angles, and same-side exterior angles. Each angle type is illustrated with examples, explaining their properties and how their sizes relate to one another. Viewers are encouraged to engage with the content, including completing exercises for better understanding, with a reminder to like, share, and subscribe for more educational videos.

Takeaways

• 😀 The script explains the angles formed when two parallel lines are intersected by a transversal.
• 😀 There are eight angles formed in total, which are grouped into six types of angles.
• 😀 The six types of angles are: opposite angles, alternate interior angles, alternate exterior angles, adjacent interior angles, adjacent exterior angles, and vertically opposite angles.
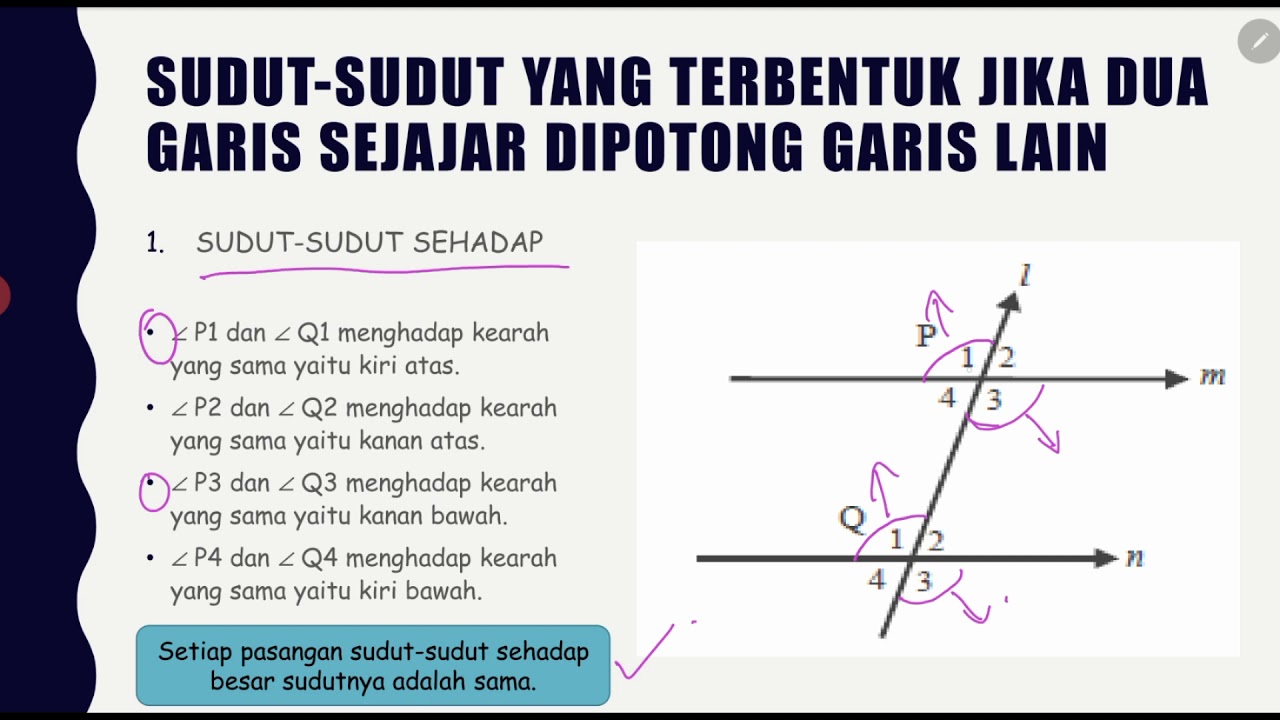
• 😀 Opposite angles have the same measure and are positioned across from each other.
• 😀 Alternate interior angles, located between the parallel lines, are equal to each other.
• 😀 Alternate exterior angles, found outside the parallel lines, are also equal.
• 😀 Adjacent interior angles, on the same side of the transversal, add up to 180°.
• 😀 Adjacent exterior angles, outside the parallel lines and on the same side of the transversal, also sum to 180°.
• 😀 Vertically opposite angles, which are across from each other, have the same measure.
• 😀 The script encourages viewers to practice problems related to the angles formed by parallel lines and a transversal for better understanding.

Q & A

What are the different types of angles formed when two parallel lines are intersected by another line?

The types of angles formed are: opposite angles, adjacent angles, interior opposite angles, exterior opposite angles, interior same-side angles, and exterior same-side angles.

What is meant by 'opposite angles'?

'Opposite angles' refer to angles that are positioned across from each other at the point of intersection, and they have equal measures.

What is the relationship between 'opposite interior angles'?

Opposite interior angles are angles located on the inside of the parallel lines and across from each other. These angles are equal in size.

How are 'exterior opposite angles' related?

Exterior opposite angles are angles located on the outside of the parallel lines, across from each other. They also have equal measures.

What are 'same-side interior angles' and what is their sum?

Same-side interior angles are angles that are on the same side of the transversal and inside the parallel lines. The sum of these angles is always 180°.

What are 'same-side exterior angles' and what is their sum?

Same-side exterior angles are angles that lie on the same side of the transversal but are outside the parallel lines. Like interior same-side angles, their sum is 180°.

Can you explain what 'opposite angles' means in simpler terms?

In simpler terms, opposite angles are the angles that are directly across from each other when two lines intersect. These angles are always equal.

How do we calculate the size of an angle formed by two parallel lines intersected by another line?

To calculate the size of an angle, we use the relationship between the types of angles (e.g., opposite angles are equal, same-side angles sum to 180°) and apply the known values to determine the unknown angles.

What is the significance of 'same-side angles' summing up to 180°?

This relationship is important because it shows that same-side angles are supplementary, meaning their total measure is always 180°, which helps in solving problems involving these angles.

Why is it important to understand these angle relationships when studying parallel lines intersected by a transversal?

Understanding these relationships helps solve geometric problems more easily, as knowing that certain angles are equal or supplementary allows for quicker and more accurate calculations.