Aula de Vetores- Parte II - G. A. e A. L.

Summary

This video script delves into the geometric and algebraic aspects of vectors in two- and three-dimensional spaces. It explores the concept of vector representation using bases, particularly the canonical basis, and covers fundamental operations such as vector addition, scalar multiplication, and orthogonal projections. Through clear examples, the script illustrates how to determine vector coordinates, perform vector operations, and understand the relationship between geometric intuition and algebraic notation. This foundational explanation provides an essential understanding of vectors and their properties in both theoretical and practical contexts.

Takeaways

• 😀 Vectors are defined by their initial point at the origin and the projection of their end point onto the coordinate axes.
• 😀 The relationship between a point in space and a vector is bijective, meaning each vector corresponds to a unique point in space.
• 😀 In a 2D Cartesian plane, the standard basis vectors, I and J, define the coordinate axes: I is horizontal (X-axis) and J is vertical (Y-axis).
• 😀 Any vector in the plane can be written as a linear combination of the basis vectors I and J, with scalars representing the coordinates of the vector.
• 😀 The coordinates of a vector in a given basis are unique, allowing for the clear description of vectors in terms of their components.
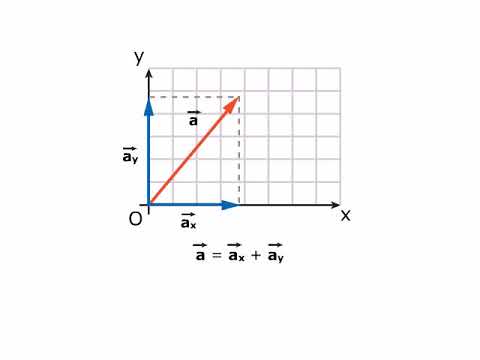
• 😀 Projections of a vector onto the coordinate axes can be used to determine its components. This involves drawing perpendicular lines to the axes.
• 😀 In vector notation, the order of the components is important when defining or comparing vectors.
• 😀 Two vectors are equal if their corresponding components in the same basis are identical (both x and y coordinates for 2D, or x, y, and z for 3D).
• 😀 Scalar multiplication of a vector involves multiplying each component of the vector by the scalar, which changes the vector's length but not its direction.
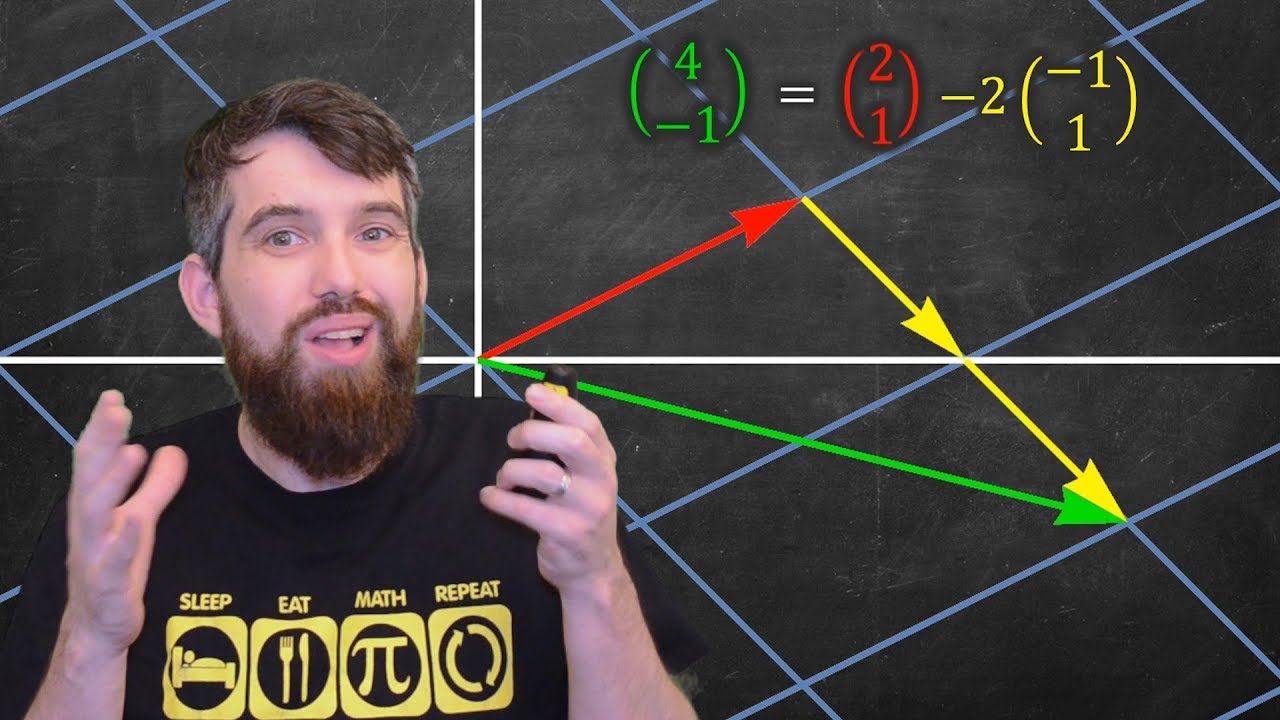
• 😀 Vector addition in algebraic terms involves adding the corresponding components of two vectors, i.e., x1 + x2 and y1 + y2 for 2D vectors.
• 😀 The concept of defining vectors using coordinates extends from 2D to 3D, where vectors are described in terms of three components (x, y, z) based on a 3D coordinate system.

Q & A

What is the main idea presented in the script regarding vectors in a coordinate system?

The script explains how to describe a vector in a coordinate system by determining its components through projections onto the X and Y axes, using orthogonal projections. The relationship between the vector and its components is bijective, meaning each vector corresponds to a unique point in the space, and vice versa.

What does 'bijection' mean in the context of vector representation?

In the context of vector representation, a bijection means that there is a one-to-one correspondence between each vector and a unique point in space. This implies that for each vector, there is exactly one point, and for each point, there is exactly one vector.

How are the unit vectors 'i' and 'j' defined in the Cartesian coordinate system?

In the Cartesian coordinate system, the unit vector 'i' is along the X-axis, with coordinates (1, 0), and the unit vector 'j' is along the Y-axis, with coordinates (0, 1). These vectors are perpendicular to each other and have a magnitude of 1.

What is the significance of the notation 'V = 3i + 2j' in the script?

The notation 'V = 3i + 2j' represents a vector 'V' expressed as a linear combination of the unit vectors 'i' and 'j'. This means that the vector 'V' can be described as having 3 units in the direction of 'i' and 2 units in the direction of 'j'.

What role does orthogonal projection play in determining the components of a vector?

Orthogonal projection is used to determine the components of a vector by projecting it onto the coordinate axes. For example, the projection of a vector onto the X-axis gives the X component, and the projection onto the Y-axis gives the Y component. These projections allow us to describe the vector's components in terms of its coordinates.

What is the concept of a 'base' in vector representation?

A 'base' refers to a set of unit vectors used to describe any vector in a given space. In the 2D Cartesian coordinate system, the base is typically represented by the unit vectors 'i' and 'j'. Any vector in this space can be expressed as a linear combination of these base vectors.

How is vector addition performed in terms of coordinates?

Vector addition is performed by adding the corresponding coordinates of the two vectors. For instance, if vector A has coordinates (x1, y1) and vector B has coordinates (x2, y2), the sum of the two vectors will have coordinates (x1 + x2, y1 + y2).

What does multiplying a vector by a scalar involve?

Multiplying a vector by a scalar involves multiplying each component of the vector by that scalar. For example, if the vector V has components (x, y) and the scalar is k, then the result of multiplying the vector by the scalar is (k * x, k * y).

What does the script explain about vector equality?

Two vectors are equal if and only if their corresponding components are equal. This means that the X and Y components of the two vectors must be identical in order for the vectors to be considered equal.

What is the relationship between vectors in a 3D space compared to 2D space, as discussed in the script?

In 3D space, vectors are described using three coordinate axes: X, Y, and Z. Just like in 2D space, vectors in 3D can be expressed as linear combinations of the unit vectors 'i', 'j', and 'k', where each component corresponds to a projection onto one of the three axes.