Simplex Method Tabular Form 01

Summary

The video explains the tabular simplex method, emphasizing that it shares the same mechanics as the algebraic simplex method, with differences primarily in presentation. It outlines the process of transforming inequalities into equalities, identifying basic variables, and iteratively updating a table to reach optimal solutions. By demonstrating the step-by-step construction of multiple tables, the video highlights how entering and leaving variables are determined, ultimately leading to an optimal solution. The conclusion reassures viewers that both methods yield equivalent results, inviting them to explore further features of the tabular simplex method in upcoming presentations.

Takeaways

• 😀 The tabular simplex method shares the same mechanics as the algebraic simplex method, differing mainly in presentation.
• 📊 Transform inequalities into equalities by adding slack variables for ≤ constraints and subtracting surplus variables for ≥ constraints.
• 📋 Construct a table with columns for each variable, placing the objective function at the top and constraints in subsequent rows.
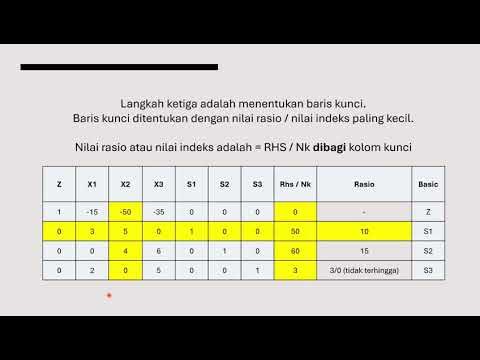
• 🔍 Basic variables are identified as those with a coefficient of 1 in their row and 0 in others, helping to determine variable values.
• 🔄 The iterative process involves selecting an entering variable with a negative coefficient and a leaving variable based on constraints limiting increase.
• 📈 The pivot row is created by dividing the entering variable's row, and operations are performed to zero out the corresponding column in other rows.
• 📑 The process continues until no negative coefficients remain in the objective function, indicating the optimal solution has been found.
• ✅ The final values of the variables can be directly read from the last table, providing the solution to the linear programming problem.
• 📊 A side-by-side comparison of algebraic equations and tabular tables shows that both methods yield equivalent results.
• 🔮 Future presentations will explore additional features of the tabular simplex method.

Q & A

What is the main focus of the presentation?

The presentation focuses on the tabular simplex method, a technique used in linear programming to solve optimization problems.

How does the tabular simplex method differ from the algebraic simplex method?

While the mechanics of both methods are the same, the tabular simplex method presents information in a table format, making it easier to visualize and manipulate.

What is the first step in using the simplex method?

The first step is to transform each inequality constraint into an equality by adding slack variables or subtracting surplus variables.

What role do basic variables play in the simplex method?

Basic variables are key to identifying the solution; they have a coefficient of 1 in one row of the tableau and 0 in other rows, indicating their status in the current solution.

What is a pivot row, and why is it important?

A pivot row is the row corresponding to the entering variable. It is used to update the tableau through row operations, ensuring that the new basic variable is correctly represented.

How do you determine which variable will enter the basis next?

You look for the most negative coefficient in the objective function row; the variable associated with this coefficient will enter the basis next.

What indicates that the simplex method has reached a final solution?

The method is complete when there are no negative coefficients left in the objective function row, indicating that an optimal solution has been reached.

What is the significance of performing row operations in the tableau?

Row operations are essential for maintaining the correct relationships among variables while introducing new basic variables and eliminating others.

Can you explain what slack and surplus variables are?

Slack variables are added to 'less than or equal to' constraints to convert them to equalities, while surplus variables are subtracted from 'greater than or equal to' constraints for the same purpose.

Why does the presenter encourage comparing the algebraic and tabular methods?

The comparison highlights that both methods produce equivalent results, reinforcing the understanding that the difference lies only in the presentation of the information.