Program Linear Metode Simpleks Soal Cerita 3 Variabel

Summary

In this video, Hotul Sinaga explains the Simplex method, an algorithm used to solve linear programming problems aimed at optimizing outcomes such as maximizing or minimizing profits. The script covers how to apply this method to a bakery's bread production scenario, involving resource constraints like flour, sugar, and butter. It walks through the steps of converting the problem to standard form, creating the Simplex table, and iterating for an optimal solution. Additionally, the video shows how to use the QM for Windows software to solve the same problem, confirming the manual solution. The result is maximizing profit while efficiently managing resources.

Takeaways

• 😀 The Simplex Method is an algorithm used to solve linear programming problems for maximization and minimization with multiple variables.
• 😀 The method involves three key steps: converting to standard form, creating a Simplex table, and performing iterations to find the optimal solution.
• 😀 The bakery example involves maximizing profit from producing three types of bread (sweet, plain, and chocolate), each requiring different amounts of ingredients.
• 😀 The objective function for the bakery problem is to maximize profit: Z_max = 5000X1 + 6000X2 + 4000X3, where X1, X2, and X3 are the quantities of sweet, plain, and chocolate bread, respectively.
• 😀 The constraints for the bakery problem are based on ingredient limitations: flour, sugar, and butter, with specific quantities available each day.
• 😀 Converting the problem to standard form includes adding slack variables (S1, S2, S3) to transform inequalities into equations.
• 😀 The Simplex table helps organize the problem's data, with rows representing variables and columns representing different coefficients and constants.
• 😀 Iteration in the Simplex Method involves selecting a pivot column and row, performing calculations, and updating the table until the optimal solution is reached.
• 😀 The method continues iterations until all coefficients in the objective function are non-negative, indicating the optimal solution is found.
• 😀 Using QM for Windows software, the same bakery problem was solved efficiently, providing results consistent with the manual calculations, demonstrating the software's effectiveness for solving linear programming problems.

Q & A

What is the Simplex method used for?

The Simplex method is an algorithm used to solve linear programming problems, particularly for finding optimal solutions for maximization or minimization objectives involving two or more variables.

What are the main steps involved in solving a linear programming problem using the Simplex method?

The main steps include: 1) converting the problem into standard form, 2) creating the Simplex table, and 3) performing iterations to find the optimal solution.

What is the objective function in the given bakery problem?

The objective function is to maximize the profit, which is represented as ZMAX = 5000X1 + 6000X2 + 4000X3, where X1, X2, and X3 represent the quantities of sweet bread, white bread, and chocolate bread, respectively.

How do you convert the problem into standard form in the Simplex method?

To convert the problem into standard form, we first express the objective function and constraints, and then introduce slack variables (S1, S2, S3) to convert the inequalities into equalities.

What are the constraints in the bakery problem?

The constraints in the bakery problem are based on the available amounts of flour, sugar, and butter. They are: 200X1 + 250X2 + 150X3 ≤ 10,000 (flour), 100X1 + 50X2 + 75X3 ≤ 5,000 (sugar), and 50X1 + 60X2 + 100X3 ≤ 3,000 (butter).

Why do we use slack variables in the Simplex method?

Slack variables are used to convert the inequality constraints into equality constraints, which are required for the Simplex method to work properly.

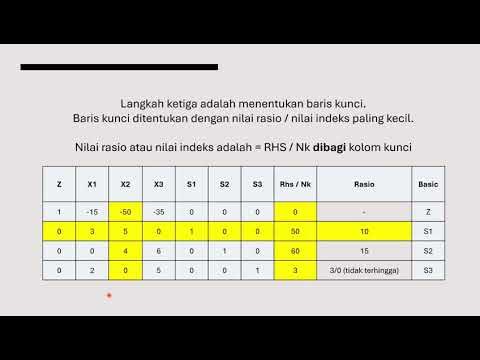
What does the iteration process in the Simplex method involve?

Iteration involves identifying the most negative value in the objective function row, selecting the pivot column, determining the pivot row through ratios, and updating the table. This process is repeated until the objective function's row contains no negative values, indicating an optimal solution.

What is the role of the 'pivot column' and 'pivot row' in the Simplex method?

The pivot column is selected based on the most negative coefficient in the objective function row, indicating the entering variable. The pivot row is determined by calculating the ratios of the right-hand side values divided by the corresponding coefficients in the pivot column, indicating the leaving variable.

How is the optimal solution determined in the Simplex method?

The optimal solution is reached when all the coefficients in the objective function row are non-negative. At this point, the current values in the Simplex table provide the optimal values for the decision variables.

How does the QM for Windows application assist in solving the linear programming problem?

The QM for Windows application automates the Simplex method by allowing users to input the objective function, constraints, and variables. It then performs the necessary calculations and iterations, providing the optimal solution that matches the manual method.