Derivada del cociente de dos funciones (u/v)
Summary
TLDREn este video, se explica cómo derivar el cociente de dos funciones utilizando la fórmula adecuada. El presentador desglosa el proceso paso a paso, comenzando por identificar el numerador y el denominador de la función. Se derivan cada uno de los términos, aplicando las reglas de derivación, y se realizan multiplicaciones y restas para simplificar el resultado final. Con un ejemplo práctico de derivar la función (5x + 2) / (3x + 8), el video proporciona una comprensión clara de cómo aplicar las técnicas de cálculo diferencial de manera efectiva.
Takeaways
- 😀 Bienvenida a la continuación del tema de cálculo diferencial.
- 📐 Se aborda la derivada del cociente de dos funciones.
- 📝 Fórmula de la derivada de un cociente: (u/v)' = (v * u' - u * v') / v^2.
- 🔍 Ejemplo práctico: derivar la función (5x + 2) / (3x + 8).
- 📊 Identificación de funciones: u = 5x + 2, v = 3x + 8.
- ➕ Derivadas calculadas: u' = 5, v' = 3.
- 🔄 Aplicación de la fórmula para obtener la derivada.
- ✏️ Se realizan multiplicaciones y simplificaciones en el proceso.
- 🧮 Resultado final de la derivada: (34) / (3x + 8)^2.
- 👋 Cierre del tema con un saludo a los amigos.
Q & A
¿Cuál es el tema principal de la sesión?
-La sesión se centra en la derivada del cociente de dos funciones en cálculo diferencial.
¿Cuál es la fórmula para derivar el cociente de dos funciones?
-La fórmula es: d/dx(u/v) = (v * du/dx - u * dv/dx) / v^2.
¿Cómo se identifica el numerador y el denominador en el ejemplo proporcionado?
-En el ejemplo, el numerador es 5x + 2 y el denominador es 3x + 8.
¿Qué es lo primero que se hace al aplicar la fórmula de derivación?
-Se identifican las funciones u y v y se encuentran sus derivadas.
¿Cuál es la derivada de 5x y por qué?
-La derivada de 5x es 5 porque se utiliza la regla de derivación de una constante multiplicada por x.
¿Qué ocurre con la derivada de una constante?
-La derivada de una constante es 0, por lo que la derivada de 2 es 0.
¿Cuál es el resultado de la multiplicación de los términos al aplicar la fórmula?
-Se obtiene 15x + 40 - 15x - 6, que simplificado es 34.
¿Cómo se simplifica el resultado final?
-El resultado se simplifica a 34 sobre (3x + 8)^2 después de restar los términos.
¿Cuál es el resultado final de la derivada en el ejemplo?
-El resultado final de la derivada es 34 / (3x + 8)^2.
¿Cuál es la importancia de entender cómo derivar el cociente de dos funciones?
-Es importante porque permite resolver problemas más complejos en cálculo y aplicaciones en diversas áreas de las matemáticas y la física.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Derivada de un cociente | Reglas de derivación

Derivada de un producto o multiplicación de funciones. Cálculo diferencial
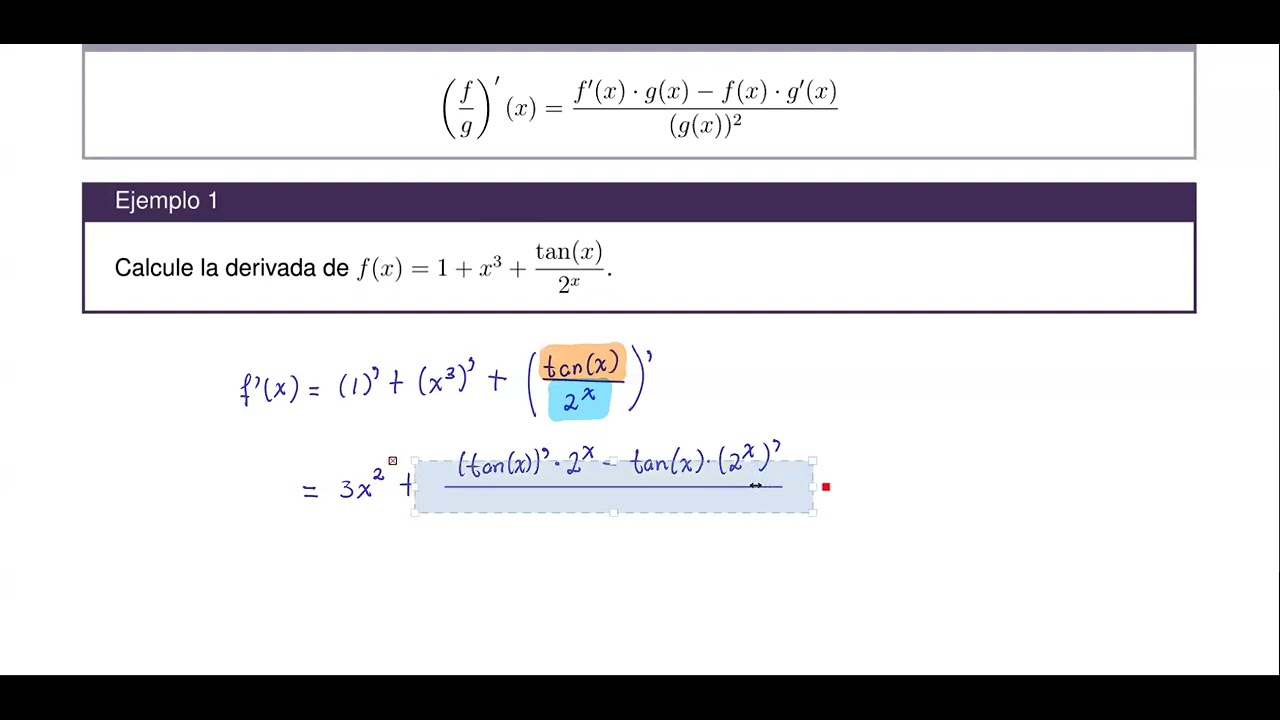
Derivadas (Regla del cociente) 1

CÓMO SE DERIVADA UNA FUNCIÓN PARAMÉTRICA - DERIVADA de FUNCIÓN PARAMÉTRICA #2

Derivadas de orden superior - Ej. 2

REGLAS DE DERIVACIÓN - Repaso en 7 minutos con ejemplos
5.0 / 5 (0 votes)
