REGLAS DE DERIVACIÓN - Repaso en 7 minutos con ejemplos
Summary
TLDREste video ofrece una explicación rápida sobre cómo derivar funciones utilizando las principales reglas de derivación: la potencia, la cadena, el producto y el cociente. A través de ejemplos sencillos, se muestra cómo aplicar cada una de estas reglas para encontrar derivadas de polinomios y otras funciones. Además, el video enfatiza la importancia de la práctica constante para dominar el cálculo diferencial, invitando a los espectadores a seguir practicando y explorando más contenido en el canal para mejorar su comprensión del tema.
Takeaways
- 📘 La derivada de una función se calcula utilizando diversas reglas y fórmulas, entre ellas la potencia, cadena, producto y cociente.
- 🔑 La regla de la potencia es esencial para derivar funciones, trabajando con el exponente de cada término.
- ✏️ En un polinomio, cada término se deriva de forma independiente bajando el exponente y restando uno.
- ⚖️ Las constantes en una función tienen derivada igual a cero.
- 🔗 La regla de la cadena se aplica cuando una función está elevada a un exponente, combinando potencia y la derivada interna.
- 📐 Después de derivar utilizando la regla de la cadena, se pueden simplificar las expresiones con operaciones algebraicas.
- ✍️ La regla del producto se usa cuando hay dos funciones multiplicándose, derivando cada una por separado.
- 📊 En la regla del cociente, se deriva el numerador y el denominador por separado, aplicando luego la fórmula del cociente.
- 🧮 La simplificación de las expresiones derivadas es crucial para obtener la forma final de la solución.
- 💡 Para dominar las derivadas, se recomienda practicar más ejercicios y repasar las reglas constantemente.
Q & A
¿Cuáles son las reglas principales para calcular la derivada de una función?
-Las reglas principales para calcular derivadas son la regla de la potencia, la regla de la cadena, la regla del producto y la regla del cociente.
¿Cómo se aplica la regla de la potencia en una función polinómica?
-En la regla de la potencia, se baja el exponente y se multiplica por el coeficiente de la variable. Luego, al exponente se le resta 1. Por ejemplo, para 3x^4, la derivada sería 12x^3.
¿Qué sucede con las constantes al calcular su derivada?
-La derivada de una constante es siempre cero, ya que las constantes no cambian con respecto a la variable.
¿Cómo se utiliza la regla de la cadena?
-La regla de la cadena se usa cuando hay una función elevada a un exponente. Primero se aplica la regla de la potencia al exponente externo y luego se deriva la función interna usando las reglas correspondientes.
¿Cuál es el procedimiento para derivar una función compuesta usando la regla de la cadena?
-Primero, se deriva la función externa utilizando la regla de la potencia, luego se deriva la función interna aplicando la regla de la potencia u otra regla, según corresponda. Finalmente, se multiplican los resultados.
¿Cuándo se debe aplicar la regla del producto?
-La regla del producto se aplica cuando dos funciones se están multiplicando entre sí. Se deriva cada función por separado y luego se combinan los resultados según la fórmula de la regla del producto.
¿Cómo se aplica la regla del producto en la derivada de dos funciones?
-Se deriva la primera función y se multiplica por la segunda función sin derivar, luego se suma el producto de la primera función sin derivar y la derivada de la segunda función.
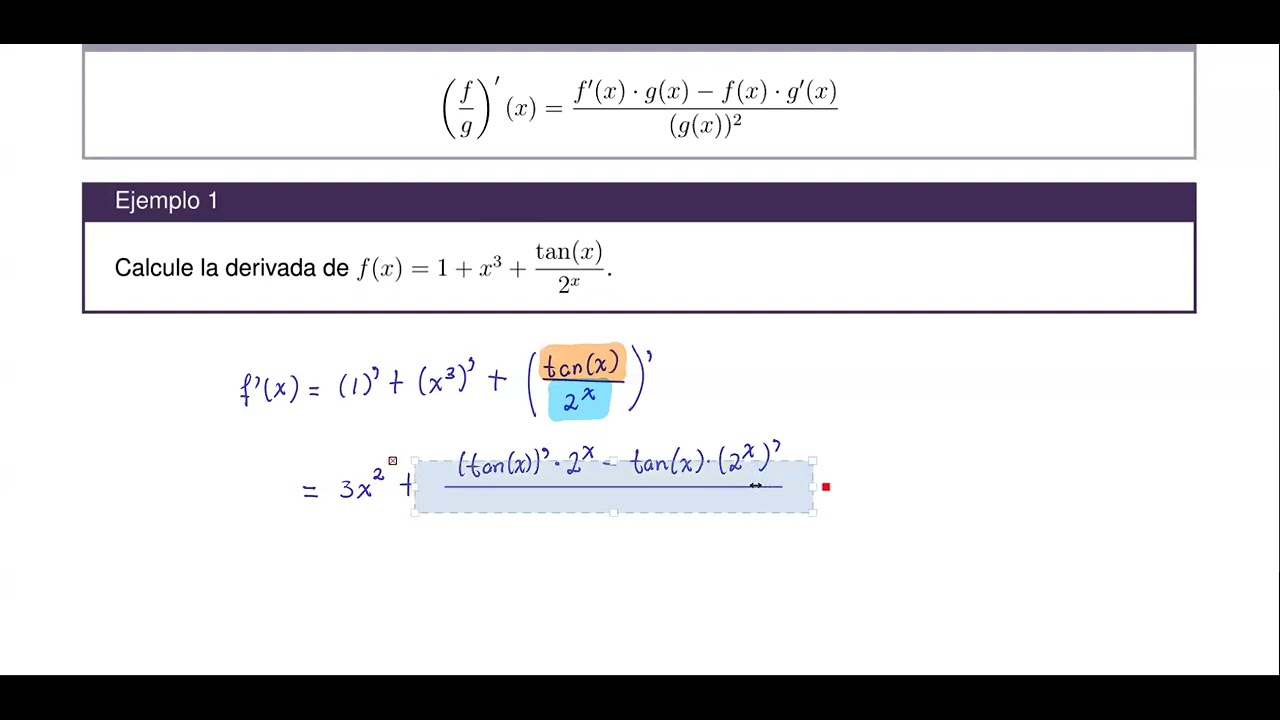
¿Qué procedimiento se sigue para derivar una función usando la regla del cociente?
-Para aplicar la regla del cociente, se deriva el numerador y se multiplica por el denominador sin derivar, luego se resta el producto del numerador sin derivar y la derivada del denominador. Finalmente, se divide todo por el denominador al cuadrado.
¿Qué importancia tienen las operaciones algebraicas al final del cálculo de la derivada?
-Las operaciones algebraicas son importantes para simplificar la expresión final de la derivada, combinando términos similares y reduciendo la fórmula derivada.
¿Qué recomendación da el instructor para dominar el cálculo de derivadas?
-El instructor recomienda practicar con muchos ejercicios para dominar el cálculo de derivadas y revisar más ejemplos para reforzar el entendimiento de las reglas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)