Restricting domain of trig function to make invertible | Trigonometry | Khan Academy
Summary
TLDRThe transcript explains how to determine the intervals where the function f(x) = cos(x - π/4) is invertible. It introduces the concept of invertibility, highlighting that a function must have a one-to-one mapping. The horizontal line test is applied to check if multiple x-values in the domain map to the same y-value in the range, making the function non-invertible. By analyzing different interval choices, the correct interval is found by ensuring the function passes the horizontal line test, meaning each range value corresponds to only one domain value.
Takeaways
- 🔄 A function is invertible when there is a one-to-one mapping between elements of the domain and range.
- 🚫 A function is not invertible if two elements from the domain map to the same element in the range.
- 🔍 The horizontal line test can be used to check if a function is invertible—if a horizontal line intersects the function graph more than once, it’s not invertible.
- 📉 The function f(x) = cos(x - π/4) fails the horizontal line test in certain intervals, making it non-invertible.
- 📝 To make the function f(x) = cos(x - π/4) invertible, we need to restrict the domain so that the horizontal line test passes.
- ❌ The interval (-5π/4, -π/4) is not valid for making the function invertible, as multiple elements map to the same range value.
- ❌ The interval [-π, π] is also invalid because it doesn’t pass the horizontal line test.
- ❌ The interval [-π/2, π/2] is ruled out as it too fails the horizontal line test.
- ✔️ The interval (π/2, 5π/4) is valid, as it passes the horizontal line test, making the function invertible.
- 📊 The key takeaway is to find a restricted domain where the function meets the criteria for invertibility by passing the horizontal line test.
Q & A
What does it mean for a function to be invertible?
-A function is invertible if there is a one-to-one mapping between the elements of its domain and range, meaning each element of the range corresponds to exactly one element of the domain. This ensures the inverse function can map the range back to the domain.
Why is the function f(x) = cos(x - π/4) not invertible over its entire domain?
-The function is not invertible over its entire domain because there are multiple elements in the domain that map to the same element in the range. This violates the one-to-one requirement for invertibility.
How can you determine if a function is invertible by using its graph?
-You can determine if a function is invertible by applying the horizontal line test. If any horizontal line intersects the graph at more than one point, the function is not invertible over that interval.
What does the horizontal line test indicate about invertibility?
-The horizontal line test shows whether a function is one-to-one. If a horizontal line crosses the graph more than once, it means that multiple points in the domain map to the same point in the range, making the function non-invertible.
What problem arises when two domain elements map to the same range element?
-If two domain elements map to the same range element, the inverse function cannot be uniquely defined. This creates ambiguity, as it is unclear which domain element should be mapped to by the inverse function.
Why is the interval from -5π/4 to -π/4 not a valid restriction for invertibility?
-This interval is not valid because within it, a horizontal line can intersect the function at multiple points, meaning that different domain values map to the same range value. This violates the one-to-one property required for invertibility.
Why is the interval from -π to π not suitable for invertibility?
-The interval from -π to π also fails the horizontal line test because there are multiple points in the domain that map to the same value in the range, preventing the function from being invertible over this domain.
Why is the interval from -π/2 to π/2 also not a valid restriction?
-The interval from -π/2 to π/2 is not valid for invertibility because the horizontal line test shows that there are still two points in the domain that map to the same range value, making the function non-invertible.
Which interval allows the function f(x) = cos(x - π/4) to be invertible?
-The interval (π/2, 5π/4) allows the function to be invertible. Within this interval, the function passes the horizontal line test, meaning each element of the range is mapped to by only one element in the domain.
How does restricting the domain of a function help in making it invertible?
-Restricting the domain eliminates the possibility of multiple domain elements mapping to the same range element. By selecting an appropriate interval, we ensure that the function is one-to-one, thus making it invertible.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
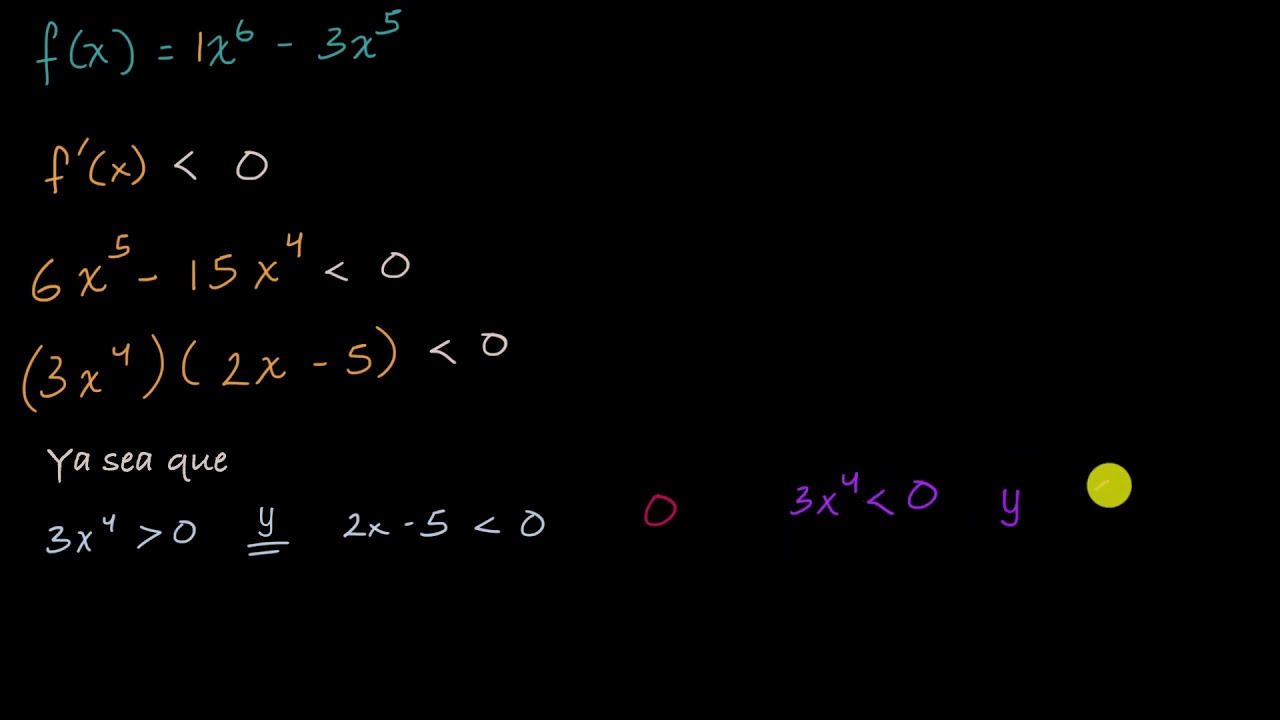
Encontrar el intervalo donde la función es decreciente | Cálculo

How to find the domain and the range of a function given its graph (example) | Khan Academy

Composite Functions
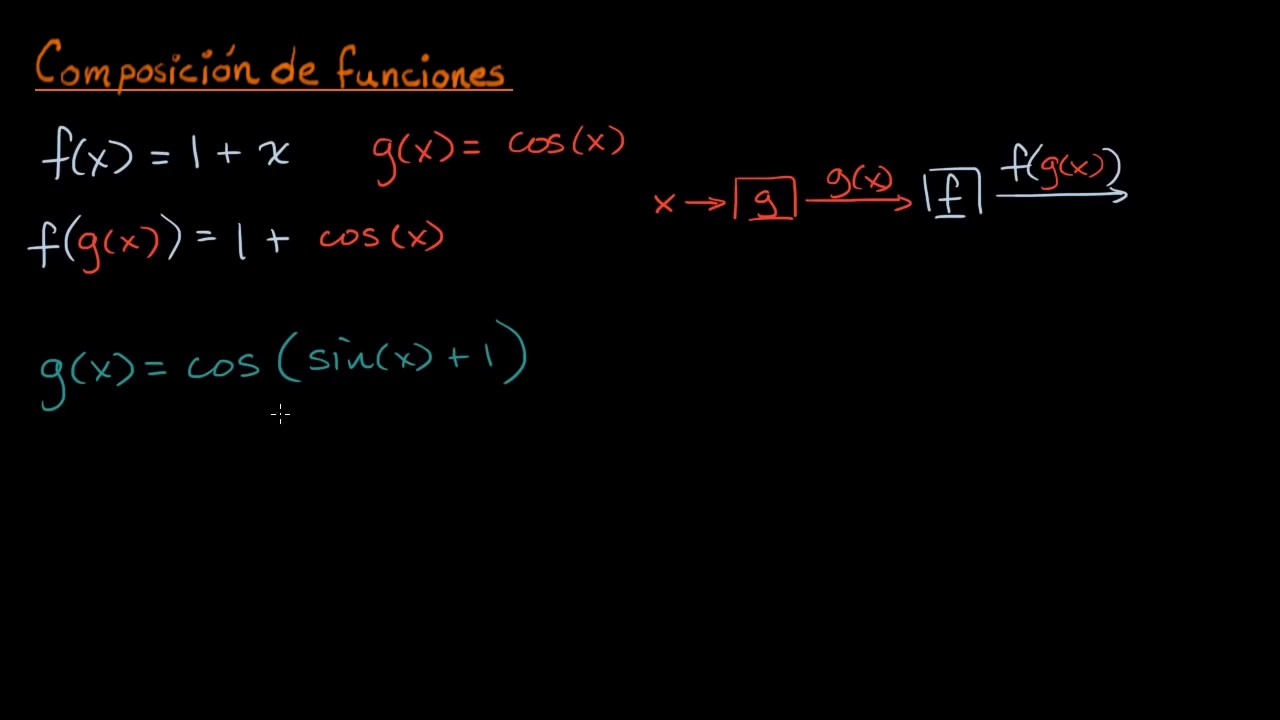
Reconocer una composición de funciones | Khan Academy en Español

Kemonotonan Fungsi Trigonometri

Composite Function | General Mathematics @MathTeacherGon
5.0 / 5 (0 votes)
